Содержание
- 2. О – начало координат (начало отсчёта); K – название системы отсчёта. Положение МТ в пространстве в
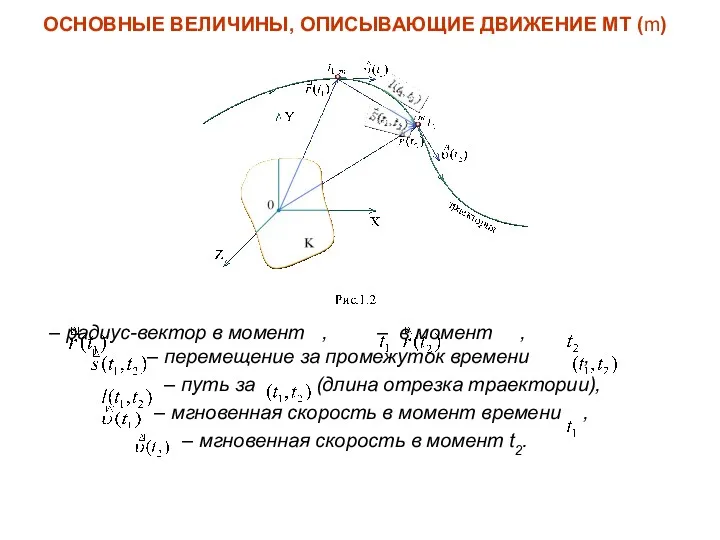
- 3. ОСНОВНЫЕ ВЕЛИЧИНЫ, ОПИСЫВАЮЩИЕ ДВИЖЕНИЕ МТ (m) – радиус-вектор в момент , – в момент , –
- 4. PS. Векторы скорости и – касательные к траектории. Очевидно: . (1.4) При малых очевидно, что .
- 5. Мгновенная путевая скорость (при ): . (1.9) Или . (1.10) Из (1.5), (1.6), (1.7а), (1.8) и
- 6. Обратно: , выполняется с помощью интегрирования. Чтобы найти по заданной , необходимо знать начальное значение ;
- 7. Векторные равенства можно записать в проекциях на оси координат: , , (1.20а,б) , , (1.21а,б) ,
- 8. 1.2. КРИВОЛИНЕЙНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ НА ПЛОСКОСТИ. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ: ТАНГЕНЦИАЛЬНОЕ И НОРМАЛЬНОЕ УСКОРЕНИЯ. Итак
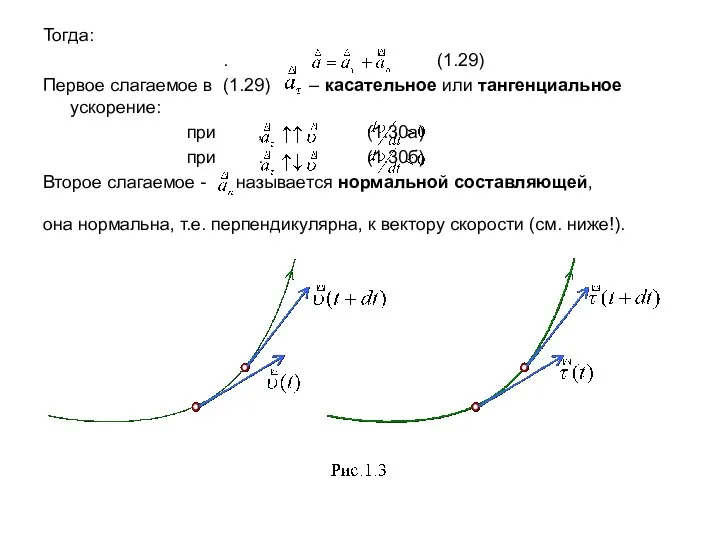
- 9. Тогда: . (1.29) Первое слагаемое в (1.29) – касательное или тангенциальное ускорение: при , (1.30а) при
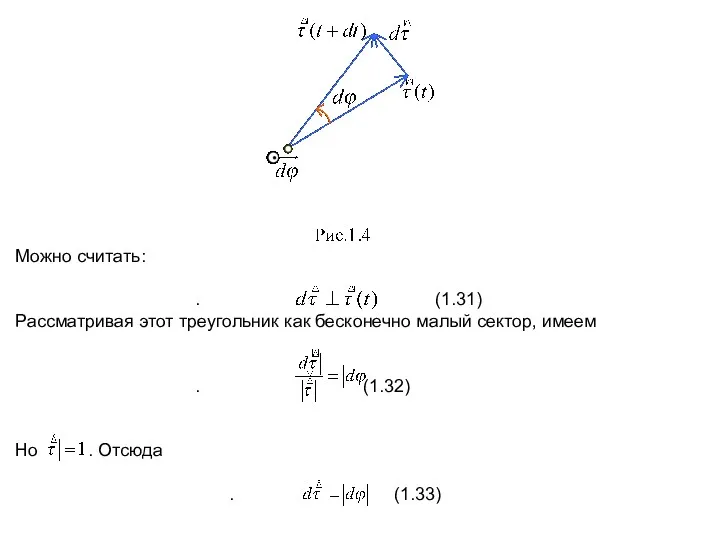
- 10. Можно считать: . (1.31) Рассматривая этот треугольник как бесконечно малый сектор, имеем . (1.32) Но .
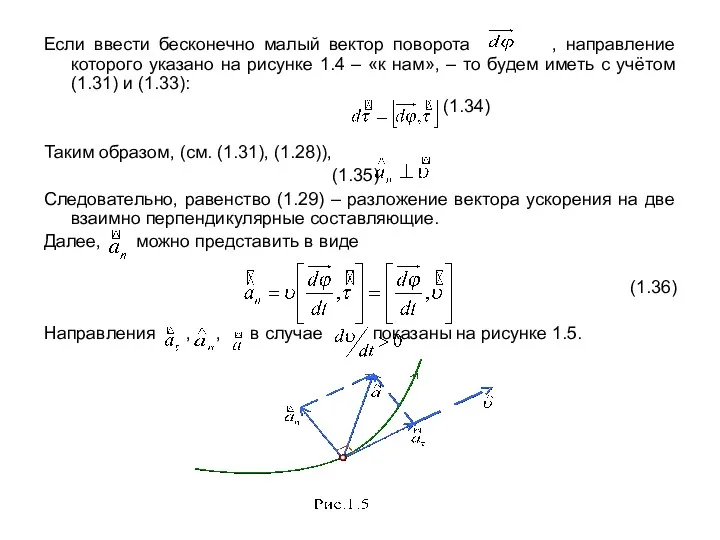
- 11. Если ввести бесконечно малый вектор поворота , направление которого указано на рисунке 1.4 – «к нам»,
- 12. Если считать малый отрезок криволинейной траектории частью окружности, то величина (1.37) называется вектором угловой скорости. Вектор
- 13. 1.3 НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГЛОВАЯ СКОРОСТЬ И УГЛОВОЕ УСКОРЕНИЕ. СВЯЗЬ МЕЖДУ ЛИНЕЙНЫМИ И УГЛОВЫМИ ВЕЛИЧИНАМИ.
- 14. Дифференцируя (1.41), находим ускорение: (1.42) Второе слагаемое в (1.42) ( см. (1.36) ) есть нормальное ускорение:
- 15. Теперь ускорение её запишется с учётом (1.41) в виде . (1.46) Двойное векторное произведение в (1.46)
- 16. Рассмотрим аналогию между ускоренными прямолинейным и криволинейным движениями (на примере МТ, движущейся по окружности). Ось OZ
- 17. Для движения по окружности: , . (1.52а, б) Равнопеременное движение вдоль оси описывается равенствами: , (1.53
- 19. Скачать презентацию












 Дисперсия света
Дисперсия света EMI introduction & Coupling modes in EMI 2018-V1
EMI introduction & Coupling modes in EMI 2018-V1 Гироскопические силы. Гироскопы и их применение в технике. Релятивистская механика. (Лекция 6)
Гироскопические силы. Гироскопы и их применение в технике. Релятивистская механика. (Лекция 6) Решение задач по ядерной физике
Решение задач по ядерной физике У кого на огороде картошка вкуснее?
У кого на огороде картошка вкуснее? галактики
галактики Введение в лабораторию
Введение в лабораторию Центр масс. Работа и энергия (лекция 3)
Центр масс. Работа и энергия (лекция 3) Презентации к некоторым лабораторным работам по учебнику А.В.Перышкина Физика 7
Презентации к некоторым лабораторным работам по учебнику А.В.Перышкина Физика 7 Конструкції кип’ятильників і водонагрівальних пристроїв
Конструкції кип’ятильників і водонагрівальних пристроїв Дисперсия света. Опыт Ньютона
Дисперсия света. Опыт Ньютона Урок по физике на тему Звуковые волны
Урок по физике на тему Звуковые волны Реактивные движения в природе
Реактивные движения в природе Конспект урока с презентацией по физике 7 класс Диффузия
Конспект урока с презентацией по физике 7 класс Диффузия Теплообмен человека с окружающей средой
Теплообмен человека с окружающей средой Электротехника. Электрические фильтры. (Лекция 11)
Электротехника. Электрические фильтры. (Лекция 11) Постоянный электрический ток
Постоянный электрический ток Оптика. Развитие взглядов на природу света
Оптика. Развитие взглядов на природу света Взаимодействие тел. Инерция. Масса тела. Сила
Взаимодействие тел. Инерция. Масса тела. Сила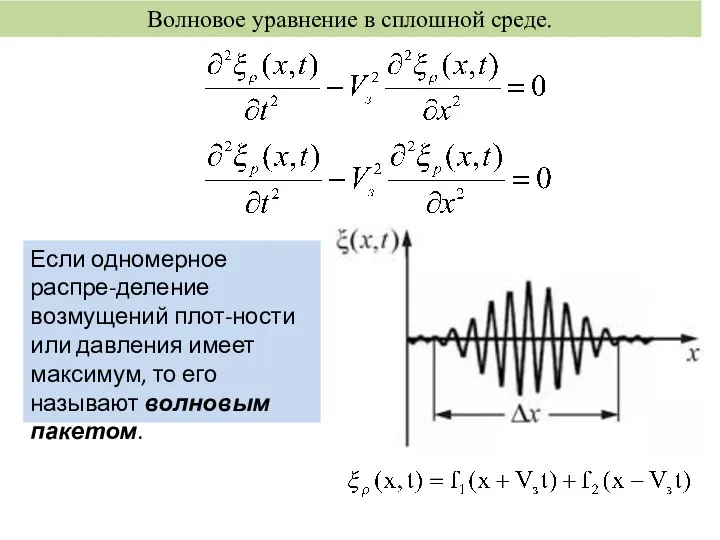 Волновое уравнение в сплошной среде
Волновое уравнение в сплошной среде Тізбек бөлігіне арналған Ом заңы
Тізбек бөлігіне арналған Ом заңы Кинематическое исследование механизмов и машин
Кинематическое исследование механизмов и машин Простейшие движения твердого тела
Простейшие движения твердого тела Исследовательское проектирование прибрежных волноэнергетических систем
Исследовательское проектирование прибрежных волноэнергетических систем Акустика как часть физики
Акустика как часть физики Тест для 8 класса Электрический ток
Тест для 8 класса Электрический ток Основы электроэнергетики
Основы электроэнергетики Агрегатные состояния вещества. Строение твердых, жидких и газообразных тел (в стихах)
Агрегатные состояния вещества. Строение твердых, жидких и газообразных тел (в стихах)