Содержание
- 2. СОДЕРЖАНИЕ ВВЕДЕНИЕ 1 МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ 1.1 Гармонические колебания 1.2 Негармонические колебания 1.3 Свободные колебания 1.4 Вынужденные
- 3. ВЕДЕНИЕ Работа посвящена изучению различных колебаний. Изучая колебания, мы будем обращать внимание не только на то,
- 4. 1 МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ Математическим маятником называют материальную точку с массой m, подвешенную на тонкой нерастяжимой невесомой
- 5. Если, сохраняя одинаковую длину маятника, подвешивать различные грузы, то период их колебаний получится одинаковым, хотя их
- 6. 1.1 Гармонические колебания Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω0 задаётся
- 7. Величина, стоящая под знаком косинуса: φ = ωt + φ0, называется фазой гармонического процесса. Смысл фазы
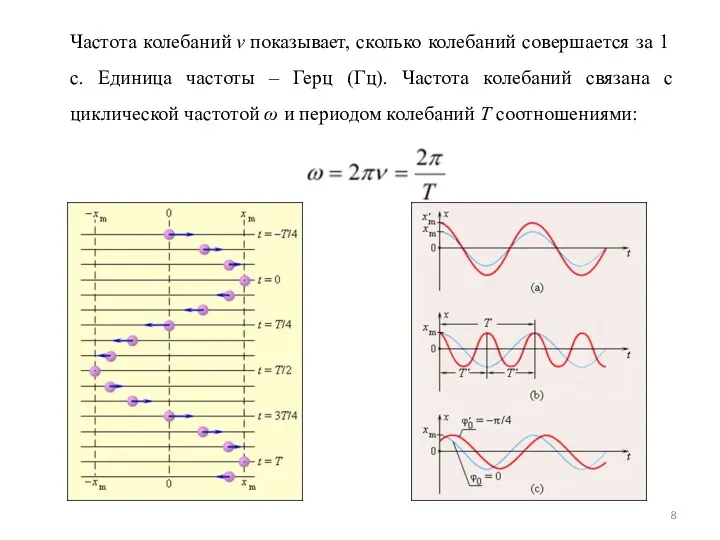
- 8. Частота колебаний ν показывает, сколько колебаний совершается за 1 с. Единица частоты – Герц (Гц). Частота
- 9. Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой: Максимальное значение скорости при гармонических
- 10. 1.2 Негармонические колебания Негармоничесие колебания – это колебания которые не происходят по закону синуса и косинуса
- 11. 1.3 Свободные колебания Колебания считают свободными (собственными) в том случае, если они выполняются только за счет
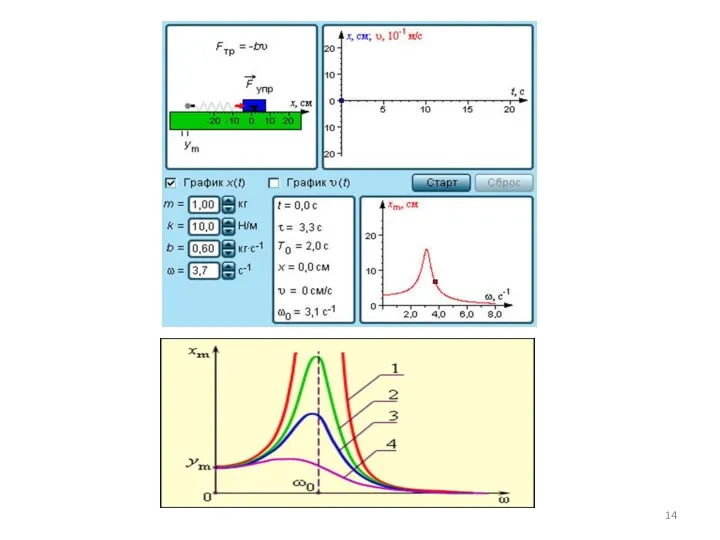
- 12. 1.4 Вынужденные колебания Колебания, совершающиеся под воздействием внешней периодической силы, называются вынужденными. В этом случае внешняя
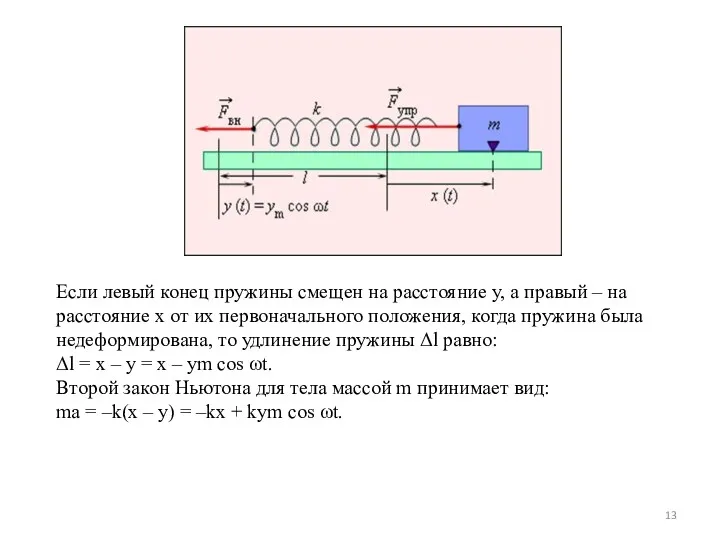
- 13. Если левый конец пружины смещен на расстояние y, а правый – на расстояние x от их
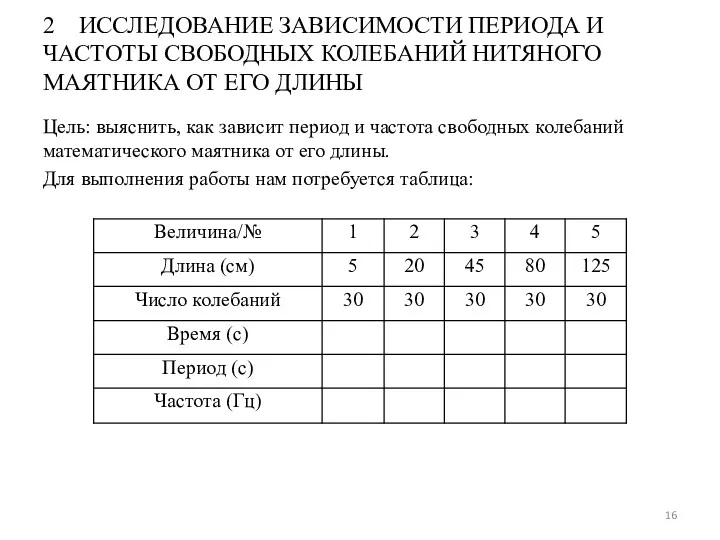
- 16. 2 ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ПЕРИОДА И ЧАСТОТЫ СВОБОДНЫХ КОЛЕБАНИЙ НИТЯНОГО МАЯТНИКА ОТ ЕГО ДЛИНЫ Цель: выяснить, как
- 17. 2.1 Проведение серии экспериментов Период колебаний: (с). Частота колебаний: (Гц), где t – это время, а
- 18. ЗАКЛЮЧЕНИЕ Нужно признать, что: период колебаний Т не зависит от массы m маятника; при небольших отклонениях
- 20. Скачать презентацию












 Фокусировка, свет. Эксплуатация вспомогательного фото-оборудования
Фокусировка, свет. Эксплуатация вспомогательного фото-оборудования Назначение, устройство и работа ГРМ легкового автомобиля на примере ВАЗ
Назначение, устройство и работа ГРМ легкового автомобиля на примере ВАЗ Основные понятия и определения
Основные понятия и определения Електромагнітні хвилі
Електромагнітні хвилі Электродинамика курсындағы қолданбалы материалдар
Электродинамика курсындағы қолданбалы материалдар Презентация по темеЭнергия. Кинетическая и потенциальная энергия. Вывод закона сохранения механической энергии
Презентация по темеЭнергия. Кинетическая и потенциальная энергия. Вывод закона сохранения механической энергии Световое загрязнение
Световое загрязнение Энергия электрического поля
Энергия электрического поля Источники электроэнергии
Источники электроэнергии Закон ома для участка цепи
Закон ома для участка цепи Закон сохранения энергии. Адиабатический процесс
Закон сохранения энергии. Адиабатический процесс Тепломассообмен. Теплообмен при кипении. (Лекция 12)
Тепломассообмен. Теплообмен при кипении. (Лекция 12) Why can we see the full moon only once a month?
Why can we see the full moon only once a month? Общее устройство тракторов
Общее устройство тракторов Закон сохранения и превращения механической энергии
Закон сохранения и превращения механической энергии Последовательное и параллельное соединение проводников
Последовательное и параллельное соединение проводников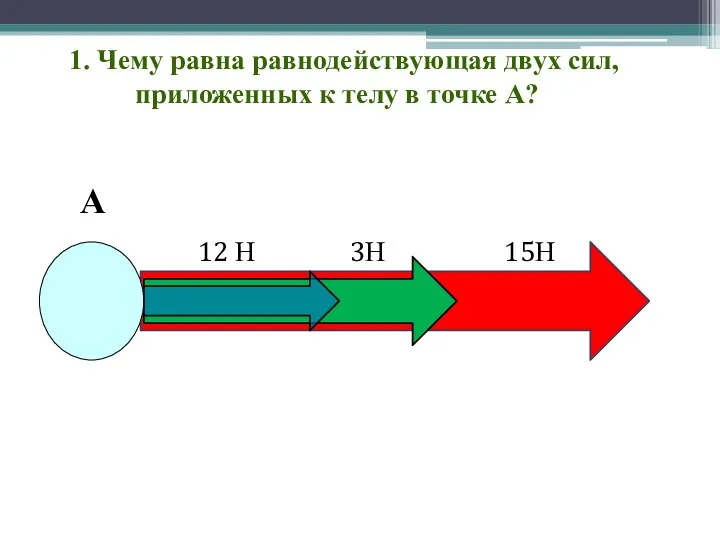 Чему равна равнодействующая двух сил, приложенных к телу в точке А?
Чему равна равнодействующая двух сил, приложенных к телу в точке А? Электрические машины постоянного тока
Электрические машины постоянного тока История развития гидравлики
История развития гидравлики Нелинейные электрические цепи постоянного тока
Нелинейные электрические цепи постоянного тока Взаимодействие тел. Второй закон Ньютона
Взаимодействие тел. Второй закон Ньютона Interest in the synthesis of metal nanoparticles by explosion
Interest in the synthesis of metal nanoparticles by explosion ПрезентацияСвет.Источники света.
ПрезентацияСвет.Источники света. Лекция №3 (3 ). Волновые уравнения электродинамики
Лекция №3 (3 ). Волновые уравнения электродинамики Свойства топлив. Теплота сгорания топлив. Урок № 4
Свойства топлив. Теплота сгорания топлив. Урок № 4 Метрология, стандартизация и сертификация. Обзорная лекция
Метрология, стандартизация и сертификация. Обзорная лекция Двупреломление. Физиологический принцип смешения окрасок
Двупреломление. Физиологический принцип смешения окрасок Силы сопротивления при движении твердых тел в жидкостях и газах
Силы сопротивления при движении твердых тел в жидкостях и газах