Содержание
- 2. Возникновение переходных процессов. Понятие о коммутации При всех изменениях в электрической цепи: включении, выключении, коротком замыкании,
- 3. Возникновение переходных процессов. Понятие о коммутации При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания,
- 4. Основные методы анализа переходных процессов в линейных цепях Классический метод, заключающийся в непосредственном интегрировании дифференциальных уравнений,
- 5. Классический метод расчета Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения
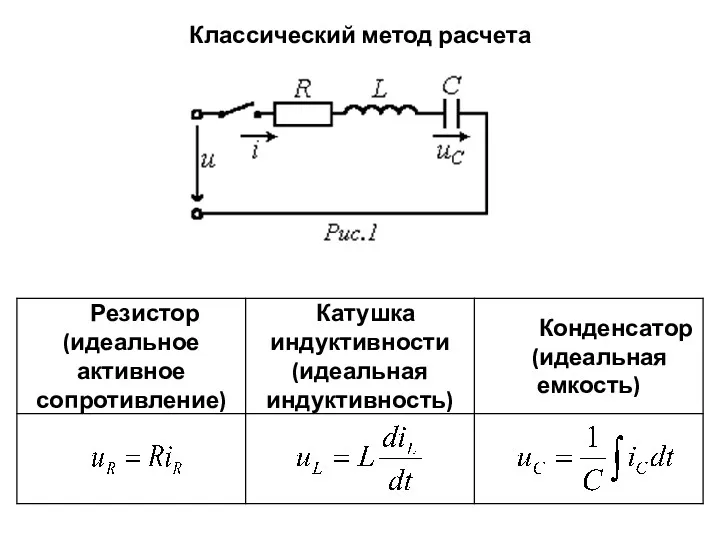
- 6. Классический метод расчета
- 7. Классический метод расчета Для последовательной цепи, содержащей линейные резистор R, катушку индуктивности L и конденсатор С,
- 8. Классический метод расчета В общем случае уравнение, описывающее переходный процесс в цепи с n независимыми накопителями
- 9. Классический метод расчета В общем случае порядок дифференциального уравнения определяется соотношением где nL и nC -
- 10. Классический метод расчета Как известно из математики, общее решение уравнения представляет собой сумму частного решения исходного
- 11. Классический метод расчета Частное решение xпр уравнения определяется видом функции f(x), стоящей в его правой части,
- 12. Классический метод расчета Вторая составляющая xсв общего решения х уравнения – решение с нулевой правой частью
- 13. Классический метод расчета Необходимо подчеркнуть, что, поскольку принцип наложения справедлив только для линейных систем, метод решения,
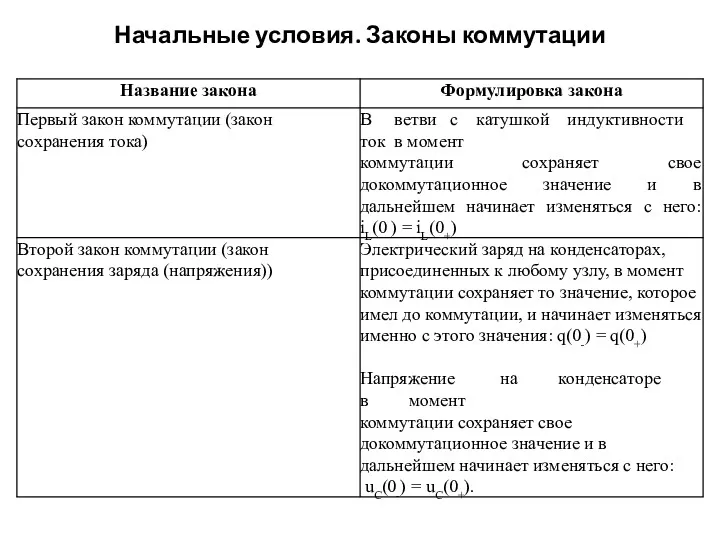
- 14. Начальные условия. Законы коммутации В соответствии с определением свободной составляющей xсв в ее выражении имеют место
- 15. Начальные условия. Законы коммутации
- 16. Начальные условия. Законы коммутации Необходимо подчеркнуть, что более общей формулировкой законов коммутации является положение о невозможности
- 17. Начальные условия. Законы коммутации Определить токи и производные di2 /dt и duC /dt в момент коммутации
- 18. Начальные условия. Законы коммутации откуда Для известных значений i1(0) и i2(0) из уравнения Определяется Значение производной
- 19. Корни характеристического уравнения. Постоянная времени Выражение свободной составляющей общего решения х дифференциального уравнения определяется видом корней
- 20. Корни характеристического уравнения. Постоянная времени Необходимо помнить, что, поскольку в линейной цепи с течением времени свободная
- 21. Корни характеристического уравнения. Постоянная времени Поскольку физически колебательный процесс связан с периодическим обменом энергией между магнитным
- 22. Корни характеристического уравнения. Постоянная времени Важной характеристикой при исследовании переходных процессов является постоянная времени τ, определяемая
- 23. ОПЕРАТОРНЫЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ
- 24. Сущность операторного метода заключается в том, что функции f(t) вещественной переменной t, которую называют оригиналом, ставится
- 25. Изображение F(p) заданной функции f(t) определяется в соответствии с прямым преобразованием Лапласа: В сокращенной записи соответствие
- 26. В качестве примера в таблице приведены изображения некоторых характерных функций, часто встречающихся при анализе нестационарных режимов.
- 27. Свойства изображений 1. Изображение суммы функций равно сумме изображений слагаемых: 2. При умножении оригинала на коэффициент
- 28. Изображения производной и интеграла В курсе математики доказывается, что если , то , где f(0) -
- 29. Изображения производной и интеграла Аналогично для интеграла: если , то С учетом ненулевых начальных условий для
- 30. Закон Ома в операторной форме Пусть имеем некоторую ветвь, выделенную из некоторой сложной цепи. Замыкание ключа
- 31. Закон Ома в операторной форме Отсюда где - операторное сопротивление рассматриваемого участка цепи.
- 32. Закон Ома в операторной форме Следует обратить внимание, что операторное сопротивление соответствует комплексному сопротивлению ветви в
- 33. Законы Кирхгофа в операторной форме Первый закон Кирхгофа: алгебраическая сумма изображений токов, сходящихся в узле, равна
- 34. Законы Кирхгофа в операторной форме При записи уравнений по второму закону Кирхгофа следует помнить о необходимости
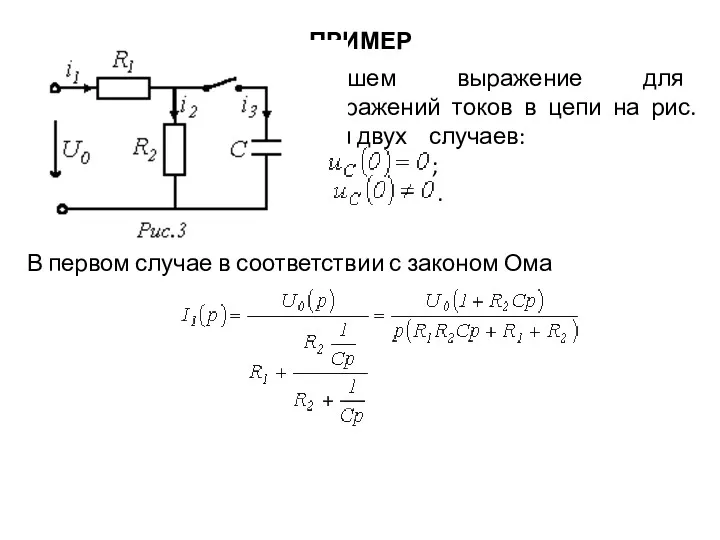
- 35. ПРИМЕР Запишем выражение для изображений токов в цепи на рис. 3 для двух случаев: 1 -
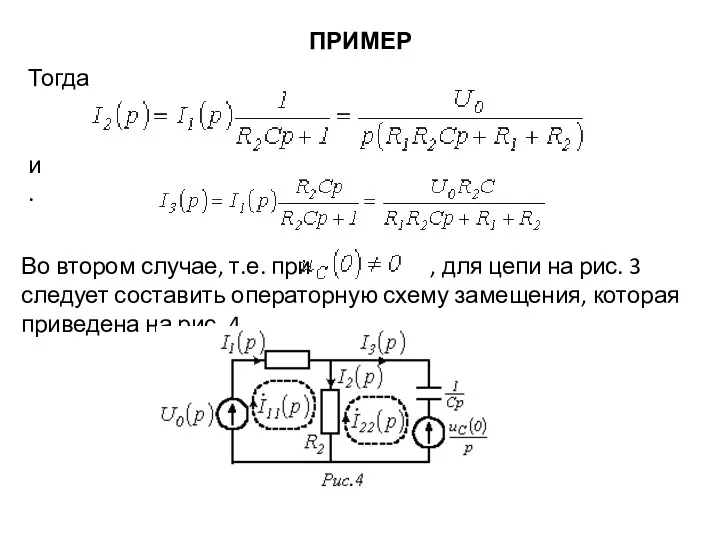
- 36. ПРИМЕР Тогда и . Во втором случае, т.е. при , для цепи на рис. 3 следует
- 37. ПРИМЕР Изображения токов в ней могут быть определены любым методом расчета линейных цепей, например, методом контурных
- 38. Переход от изображений к оригиналам Переход от изображения искомой величины к оригиналу может быть осуществлен следующими
- 39. Переход от изображений к оригиналам 2. По таблицам соответствия между оригиналами и изображениями В специальной литературе
- 40. Переход от изображений к оригиналам 3. С использованием формулы разложения Пусть изображение искомой переменной F(p) определяется
- 41. Переход от изображений к оригиналам Для определения коэффициентов Ak умножим левую и правую части соотношения (3)
- 42. Переход от изображений к оригиналам Таким образом, Поскольку отношение есть постоянный коэффициент, то учитывая, что ,
- 43. Переход от изображений к оригиналам В заключение раздела отметим, что для нахождения начального f(0) и f(∞)
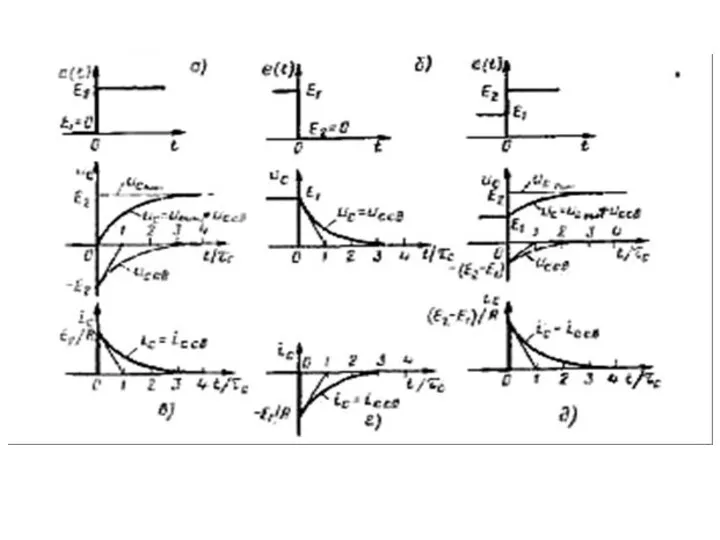
- 44. Переходные процессы в последовательной RC-цепи при скачкообразном изменении ЭДС
- 45. Переходные процессы в последовательной RC-цепи при скачкообразном изменении ЭДС
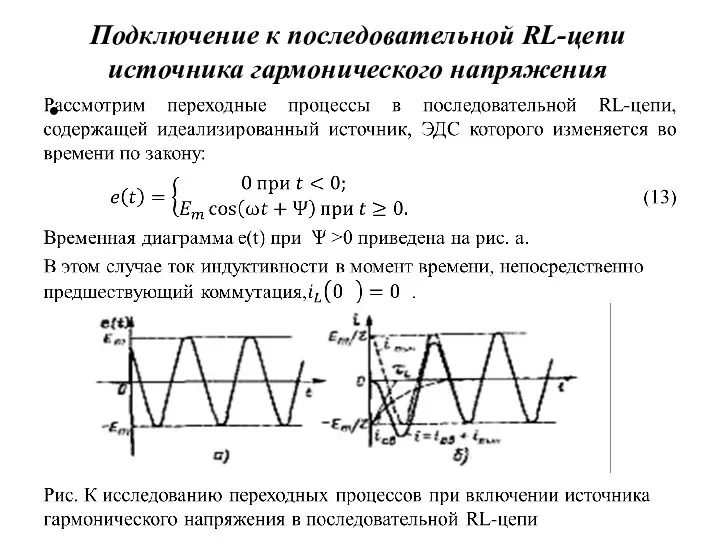
- 52. Подключение к последовательной RL-цепи источника гармонического напряжения
- 56. Скачать презентацию















































 Устройство и принципы работы жидкостного и металлического манометров
Устройство и принципы работы жидкостного и металлического манометров Деформация тела. Сила упругости. Закон Гука
Деформация тела. Сила упругости. Закон Гука Микроструктурные эффекты в порошковой дифракции и методы их описания
Микроструктурные эффекты в порошковой дифракции и методы их описания Электроразведка. Бакалавриат
Электроразведка. Бакалавриат Электромагнитная индукция
Электромагнитная индукция Паровая машина. Паровой двигатель Уатта
Паровая машина. Паровой двигатель Уатта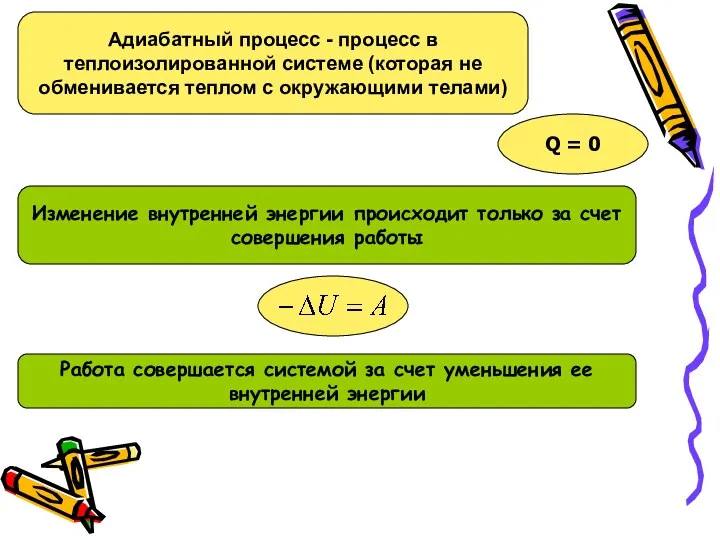 Адиабатный процесс
Адиабатный процесс Масса, плотность, объем. 7 класс
Масса, плотность, объем. 7 класс Профессия автомеханик
Профессия автомеханик Техническое обслуживание и ремонт систем энергообеспечения и запуска двигателя
Техническое обслуживание и ремонт систем энергообеспечения и запуска двигателя Електрична провідність матеріалів: провідники, напівпровідники та діелектрики. Струм у металах
Електрична провідність матеріалів: провідники, напівпровідники та діелектрики. Струм у металах Объемные резонаторы
Объемные резонаторы Әр түрлі иондаушы сәулелер көздері түрлерінің заттармен өзара әсерлесуі
Әр түрлі иондаушы сәулелер көздері түрлерінің заттармен өзара әсерлесуі Технология ультразвукового контроля узлов и агрегатов электропоезда
Технология ультразвукового контроля узлов и агрегатов электропоезда Равномерное движение по окружности
Равномерное движение по окружности Эксергетический КПД сушильной установки
Эксергетический КПД сушильной установки Реальные газы. Равновесие фаз
Реальные газы. Равновесие фаз Изобретение радио. Принципы радиосвязи. Телевидение
Изобретение радио. Принципы радиосвязи. Телевидение Урок физики в 7 классе Способы изменения давления Урок физики №32 в 7-м классе на тему Способы изменения давления
Урок физики в 7 классе Способы изменения давления Урок физики №32 в 7-м классе на тему Способы изменения давления Теплота сгорания топлива
Теплота сгорания топлива Инфракрасная спектроскопия
Инфракрасная спектроскопия Распределительное устройство 10 кВ
Распределительное устройство 10 кВ Воздухоплавание. Плавание судов
Воздухоплавание. Плавание судов Архимедова сила
Архимедова сила Соединения. Резьбовые, сварные, заклепочные, шпоночные, шлицевые, штифтовые, гладкие соединения
Соединения. Резьбовые, сварные, заклепочные, шпоночные, шлицевые, штифтовые, гладкие соединения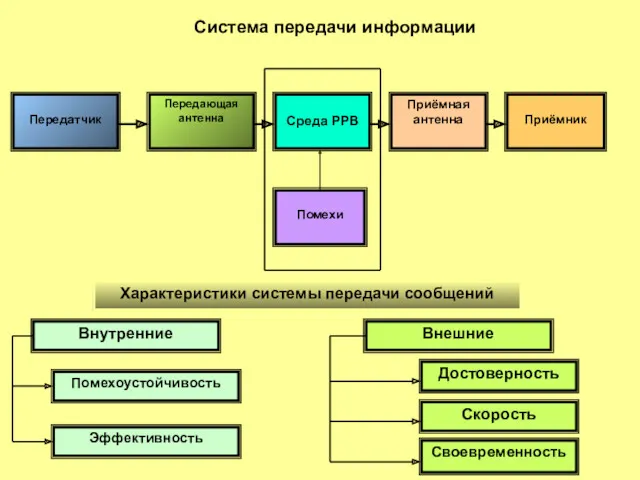 Система передачи информации
Система передачи информации Энергия топлива. Теплота сгорания топлива
Энергия топлива. Теплота сгорания топлива Смачивание и капиллярные явления. Урок 6. Физика. 8 класс
Смачивание и капиллярные явления. Урок 6. Физика. 8 класс