Содержание
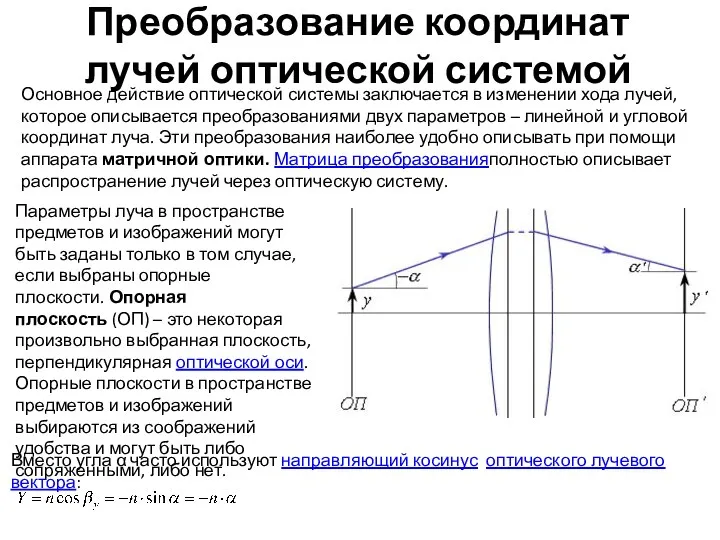
- 2. Преобразование координат лучей оптической системой Основное действие оптической системы заключается в изменении хода лучей, которое описывается
- 3. (ОС) Если оптическая система является центрированной, то a0=b0=0. Все члены ряда, начиная с a3 и b3,
- 4. Матрица преобразования лучей Все свойства идеальной оптической системы полностью описываются матрицей преобразования лучей , называемой также
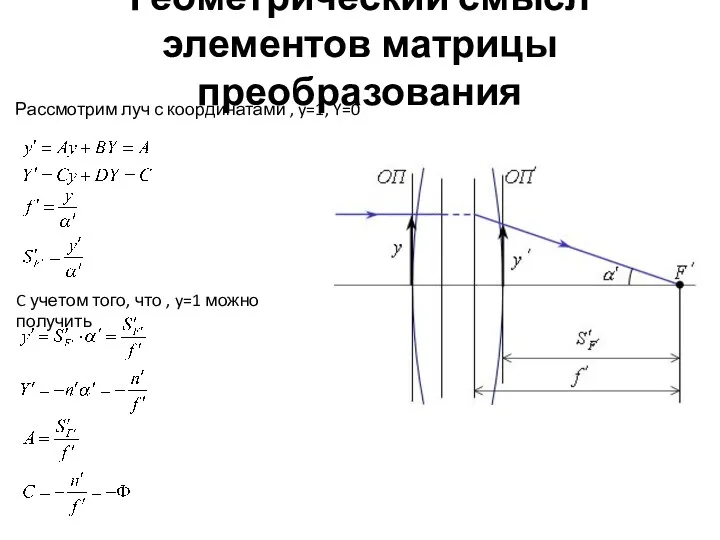
- 5. Геометрический смысл элементов матрицы преобразования Рассмотрим луч с координатами , y=1, Y=0 C учетом того, что
- 6. Геометрический смысл элементов матрицы преобразования Рассмотрим луч с координатами , Y=1 (α=-1/n), Y’=0 (α’=0) C учетом
- 7. Геометрический смысл элементов матрицы преобразования Элемент матрицы С зависит только от параметров оптической системы, а элементы
- 8. Обратная матрица преобразования - единичная матрица Обратная матрица преобразования описывает обратное преобразование (из выходных координат во
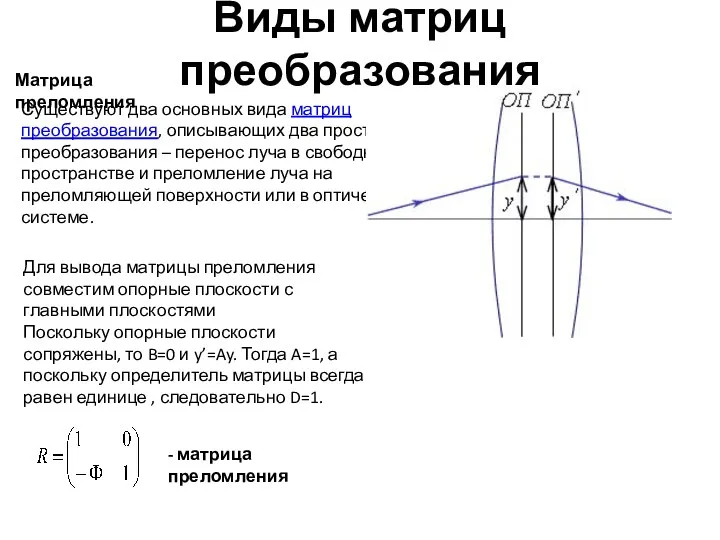
- 9. Виды матриц преобразования Для вывода матрицы преломления совместим опорные плоскости с главными плоскостями Поскольку опорные плоскости
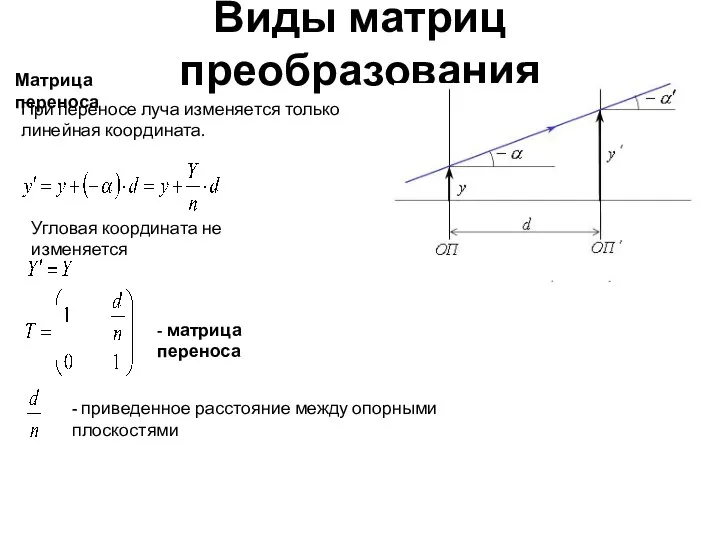
- 10. Виды матриц преобразования При переносе луча изменяется только линейная координата. Матрица переноса - матрица переноса Угловая
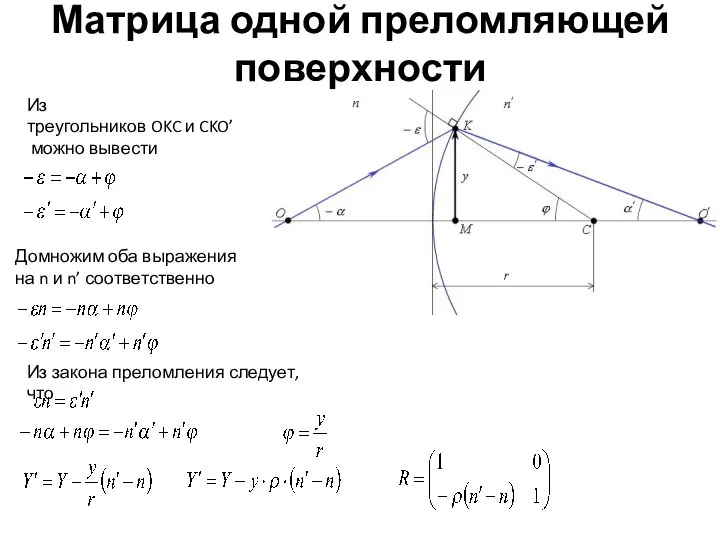
- 11. Матрица одной преломляющей поверхности Из треугольников OKC и CKO’ можно вывести Домножим оба выражения на n
- 12. Матрица зеркальной (отражающей) поверхности Для плоского зеркала Следовательно, плоское зеркало не меняет хода луча (геометрический косинус
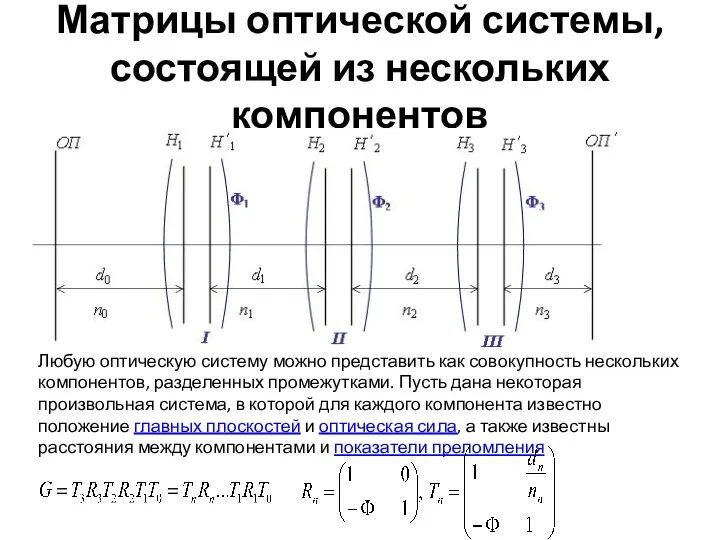
- 13. Матрицы оптической системы, состоящей из нескольких компонентов Любую оптическую систему можно представить как совокупность нескольких компонентов,
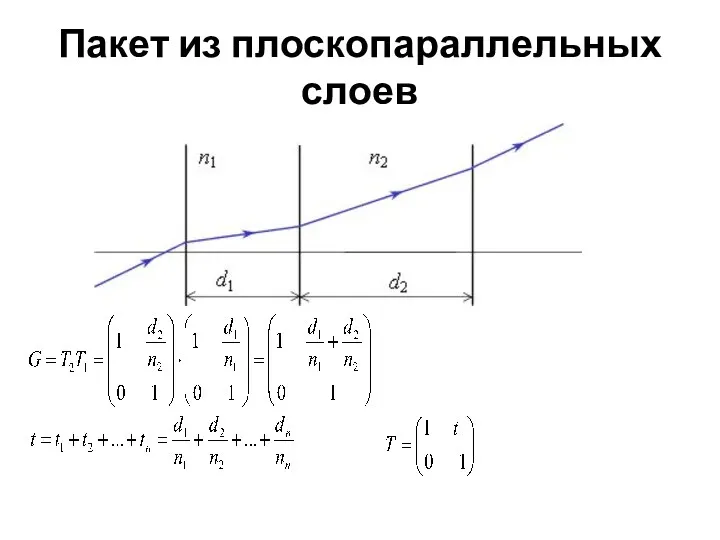
- 14. Пакет из плоскопараллельных слоев
- 15. Оптическая система с нулевыми расстояниями между компонентами то есть оптические силы таких компонент складываются
- 16. Двухкомпонентная оптическая система Рассмотрим частные случаи двухкомпонентной системы. Если d=0, тогда Ф=Ф1+Ф2. Если t=d/n=1/Ф1, это значит,
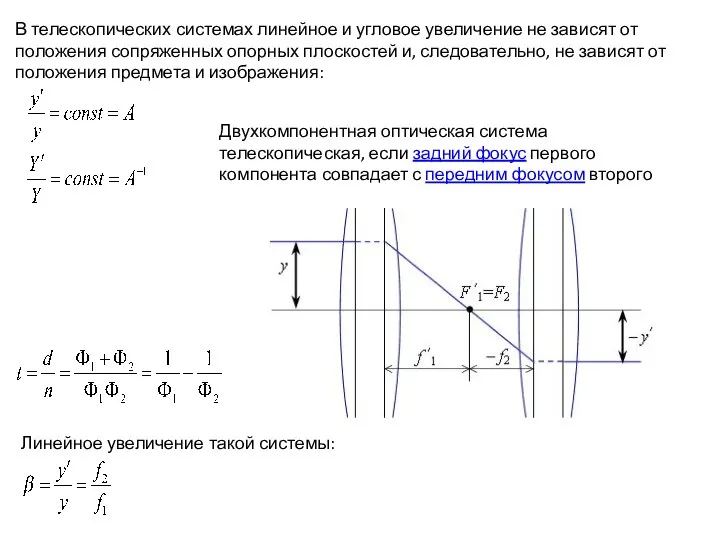
- 17. Афокальные (телескопические) системы Афокальные или телескопические системы – это системы из двух или более компонентов, оптическая
- 18. В телескопических системах линейное и угловое увеличение не зависят от положения сопряженных опорных плоскостей и, следовательно,
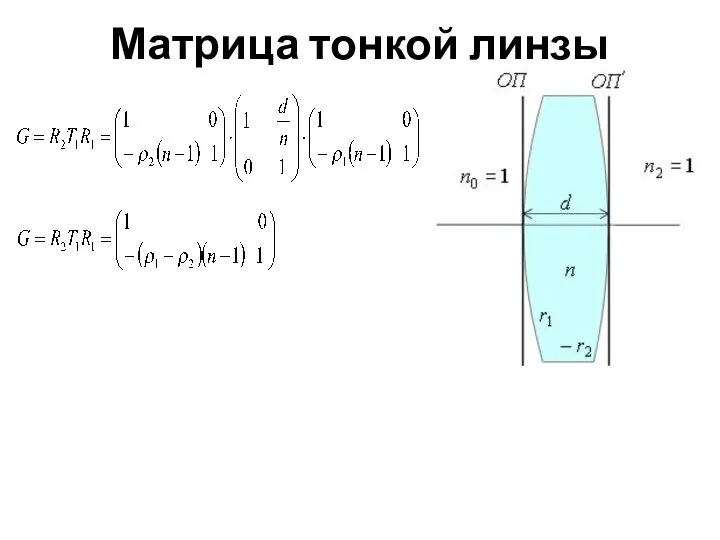
- 19. Матрица тонкой линзы
- 20. Расчет параксиальных (нулевых) лучей через оптическую систему Нулевые лучи – это лучи, которые преломляются по законам
- 23. Скачать презентацию











 Презентация с анимацией к уроку в 9 классе. Лабораторная работа №1. Исследование равноускоренного движения без начальной скорости
Презентация с анимацией к уроку в 9 классе. Лабораторная работа №1. Исследование равноускоренного движения без начальной скорости Уравнение состояния идеального газа. Газовые законы
Уравнение состояния идеального газа. Газовые законы Система стабилизации высоты полета беспилотного летательного аппарата при внешних возмущениях
Система стабилизации высоты полета беспилотного летательного аппарата при внешних возмущениях Спектроскопические методы анализа. Методы атомной и молекулярной спектроскопии
Спектроскопические методы анализа. Методы атомной и молекулярной спектроскопии Технология мини-исследования на уроках физики
Технология мини-исследования на уроках физики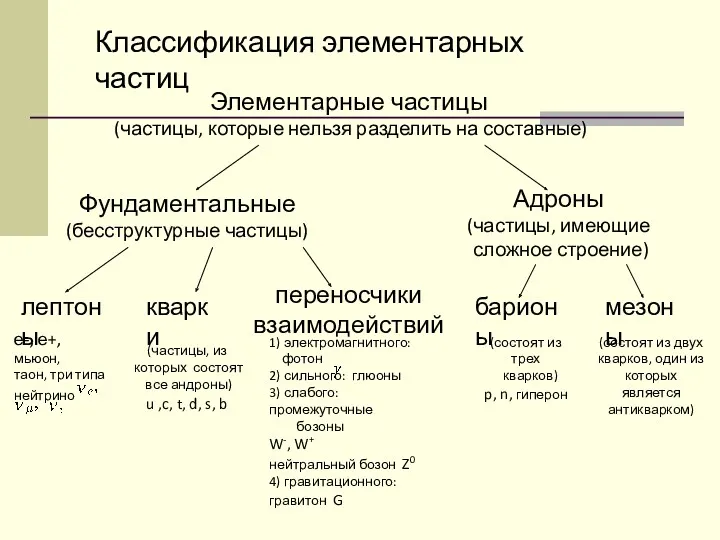 конспект урока по теме Мир элементарных частиц
конспект урока по теме Мир элементарных частиц Механика. Механическое движение
Механика. Механическое движение повтор.строение атома
повтор.строение атома Експлуатація навчального вертольота. Експлуатація фюзеляжу, несучої системи і злітно-посадкових пристроїв
Експлуатація навчального вертольота. Експлуатація фюзеляжу, несучої системи і злітно-посадкових пристроїв Електрика: промислова, статична і атмосферна
Електрика: промислова, статична і атмосферна Альтернативные источники энергии
Альтернативные источники энергии Процессы, происходящие в веществе при его бомбардировке электронами
Процессы, происходящие в веществе при его бомбардировке электронами Направление тока и направление линий его магнитного поля
Направление тока и направление линий его магнитного поля Расчет силовых нагрузок на вал и построение эпюр изгибающих моментов и крутящего момента
Расчет силовых нагрузок на вал и построение эпюр изгибающих моментов и крутящего момента Магнитное поле токов. Занятие 4
Магнитное поле токов. Занятие 4 Механическая работа. Мощность. 7 класс
Механическая работа. Мощность. 7 класс Вимірювання сили, маси, крутного моменту, нахилу і прискорення
Вимірювання сили, маси, крутного моменту, нахилу і прискорення Радиоактивность. Гипотеза об атомах
Радиоактивность. Гипотеза об атомах Дисперсия. Интерференция и дифракция света
Дисперсия. Интерференция и дифракция света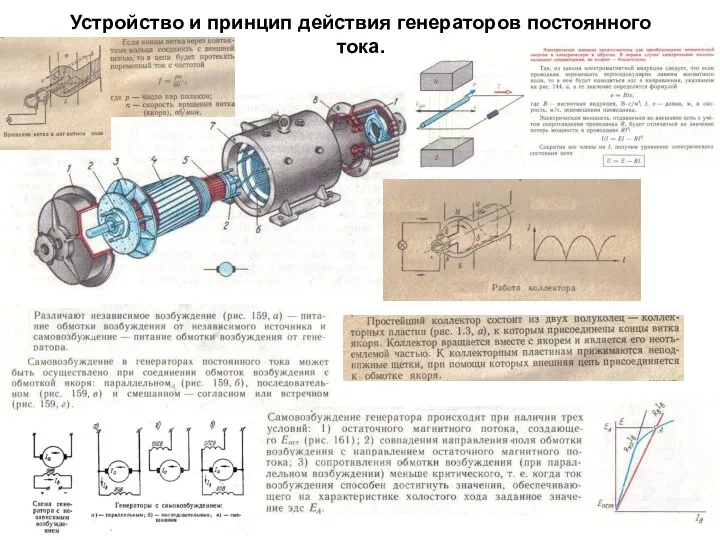 Устройство и принцип действия генераторов постоянного тока на судне. (Билет 9)
Устройство и принцип действия генераторов постоянного тока на судне. (Билет 9) Физика и безопасность дорожного движения /сценарий мероприятия и презентация/
Физика и безопасность дорожного движения /сценарий мероприятия и презентация/ Преломление света. Физический смысл показателя преломления. 9 класс
Преломление света. Физический смысл показателя преломления. 9 класс Ядерний реактор
Ядерний реактор Простые механизмы и “Золотое правило” механики
Простые механизмы и “Золотое правило” механики 1949 – 1989 - 1991
1949 – 1989 - 1991 Осмотр колесных пар
Осмотр колесных пар Прибор расходомер
Прибор расходомер Что такое сила? Вопросы для повторения
Что такое сила? Вопросы для повторения