Содержание
- 2. Оболочкой называется тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми (толщина оболочки) есть величина малая по
- 3. Будем рассматривать тонкие оболочки, у которых толщина мала по сравнению с радиусом кривизны поверхности. Если допустить
- 4. Наиболее распространенный вариант теории оболочек основан на гипотезе Кирхгофа–Лява: 1) элемент, прямолинейный и нормальный к срединной
- 5. Как при расчете балок исследование сводится к изучению одномерного объекта — оси балки, так и в
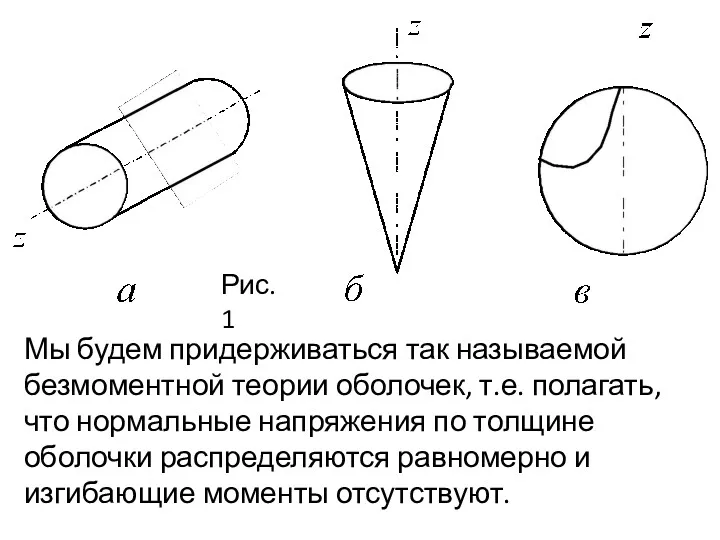
- 6. Рис.1 Мы будем придерживаться так называемой безмоментной теории оболочек, т.е. полагать, что нормальные напряжения по толщине
- 7. Условия существования безмоментного напряженного состояния следующие: 1) срединная поверхность оболочки должна быть достаточно гладкой, т.е. чтобы
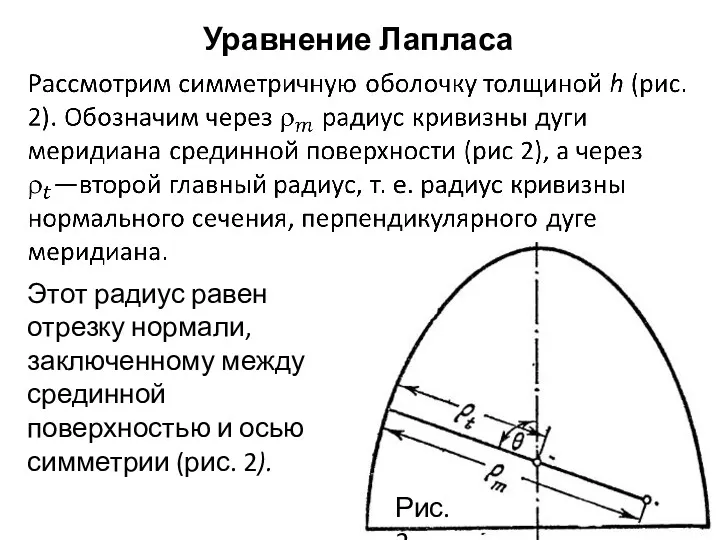
- 8. Уравнение Лапласа Рис.2 Этот радиус равен отрезку нормали, заключенному между срединной поверхностью и осью симметрии (рис.
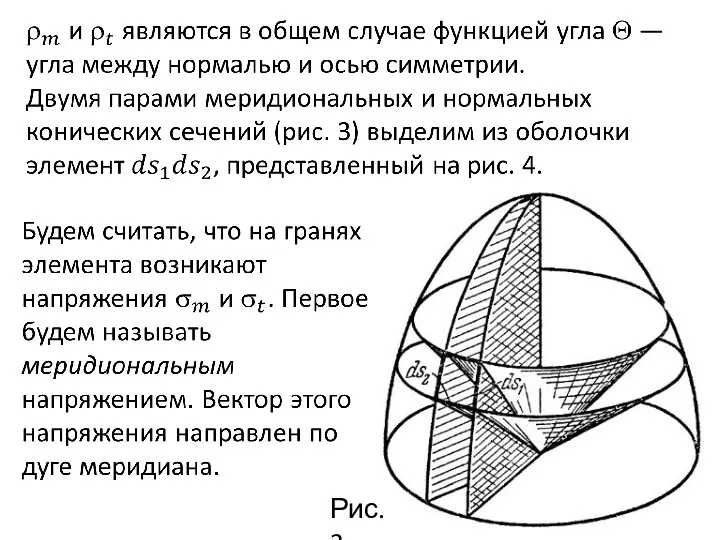
- 9. Рис.3
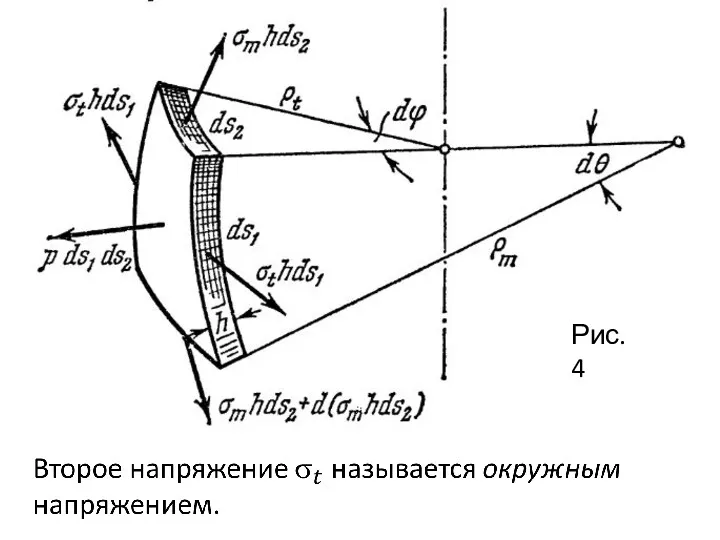
- 10. Рис.4
- 11. Нагрузку, действующую на оболочку, будем считать осесимметричной, т.е. постоянной в пределах одной параллели, и нормальной к
- 12. Спроектируем силы, действующие на элемент, на направление нормали к выделенному элементу (рис.4): Учтем, что тогда получим
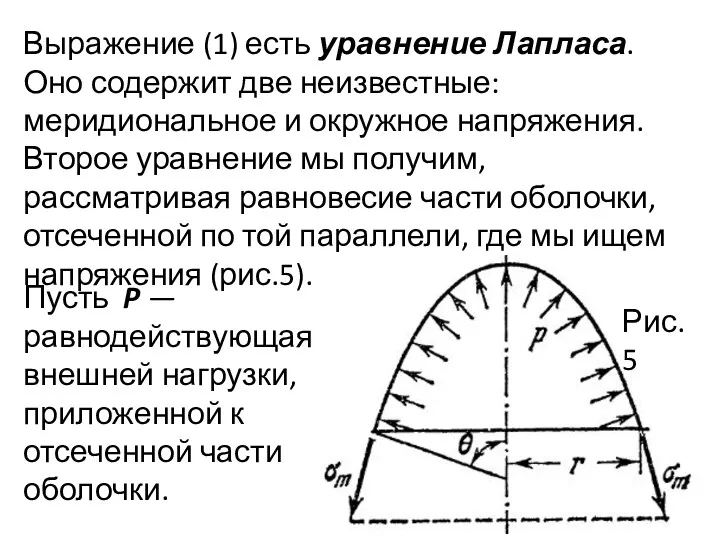
- 13. Выражение (1) есть уравнение Лапласа. Оно содержит две неизвестные: меридиональное и окружное напряжения. Второе уравнение мы
- 14. В силу осевой симметрии она направлена по оси симметрии. Проецируя силы, действующие на отсеченную часть, на
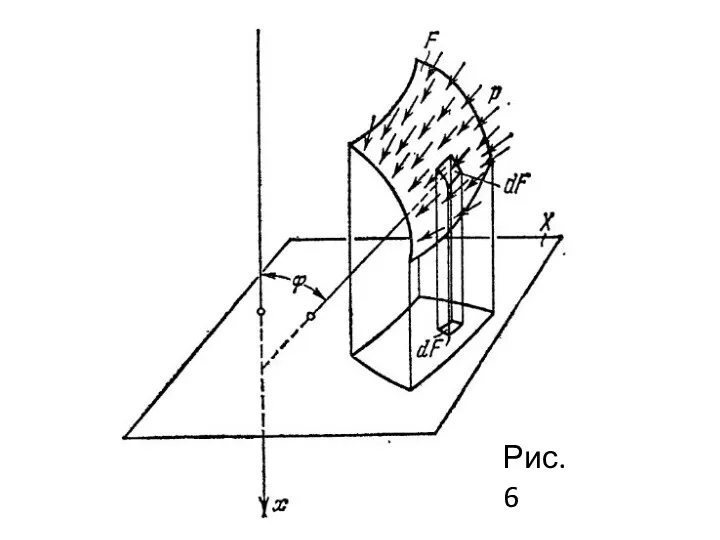
- 16. Теорема 1. Если на какую-либо поверхность действует равномерно распределенное давление, то, независима от формы поверхности, проекция
- 17. Рис.6
- 18. где ϕ - угол между нормалью к поверхности и осью x. Площадь проекции элемента dF на
- 19. Таким образом, для того чтобы определить проекцию равнодействующей сил давления на ось х, нужно предварительно спроецировать
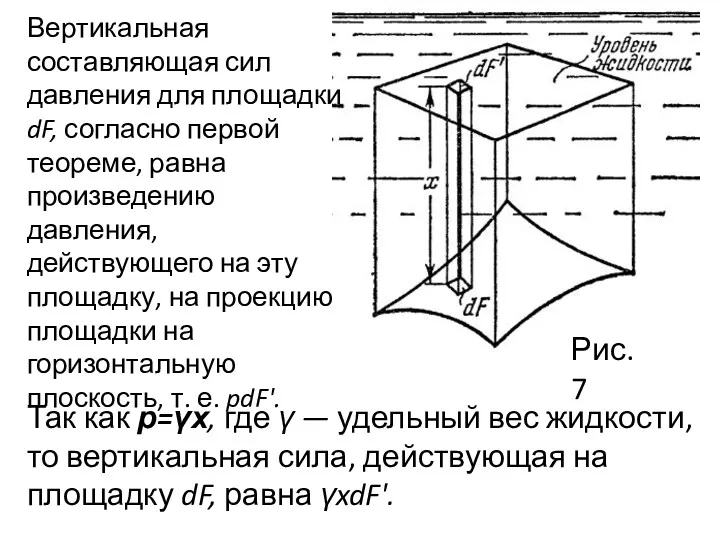
- 20. Рис.7 Вертикальная составляющая сил давления для площадки dF, согласно первой теореме, равна произведению давления, действующего на
- 21. Но xdF' — объем элементарной призмы, расположенной над площадкой dF. Суммарная искомая сила будет, следовательно, равна
- 23. Скачать презентацию













 Электромагнитные колебания
Электромагнитные колебания Общие вопросы математического описания электромеханических систем
Общие вопросы математического описания электромеханических систем Поршеньді компрессорларды жөндеу
Поршеньді компрессорларды жөндеу Первичные измерительные преобразователи тока и напряжения
Первичные измерительные преобразователи тока и напряжения Автоматтық жүйелер: негізгі анықтамалар, функционалдық схемалар. Ақпарат ұғымы, саны. Хабарлама
Автоматтық жүйелер: негізгі анықтамалар, функционалдық схемалар. Ақпарат ұғымы, саны. Хабарлама STARIA(US4)/Неисправность датчика EGTS T3
STARIA(US4)/Неисправность датчика EGTS T3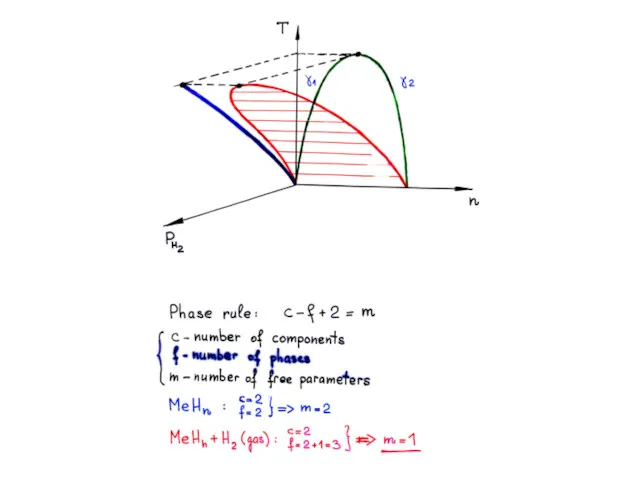 Вырожденные фазовые равновесия на экспериментальных t-x диаграммах
Вырожденные фазовые равновесия на экспериментальных t-x диаграммах Нанотехнологии и их применение
Нанотехнологии и их применение Методика проведения урока-исследования по теме Термодинамика
Методика проведения урока-исследования по теме Термодинамика Материалы и технологии изготовления нано- и микро-электромеханических систем НЭМС/МЭМС
Материалы и технологии изготовления нано- и микро-электромеханических систем НЭМС/МЭМС Физика и безопасность дорожного движения /сценарий мероприятия и презентация/
Физика и безопасность дорожного движения /сценарий мероприятия и презентация/ Биофизические основы действия ионизирующего излучения
Биофизические основы действия ионизирующего излучения Электростатика. Электризация. Заряд. Взаимодействие зарядов. Закон Кулона
Электростатика. Электризация. Заряд. Взаимодействие зарядов. Закон Кулона Использование электронных образовательных ресурсов в преподавании физики
Использование электронных образовательных ресурсов в преподавании физики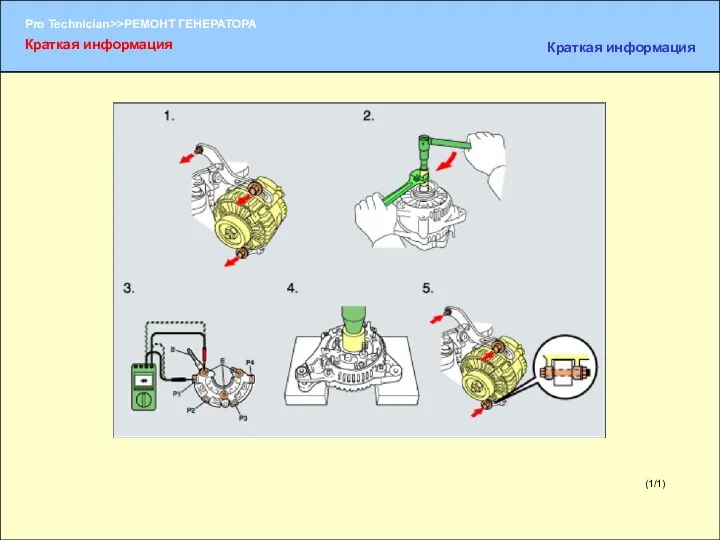 Ремонт генератора
Ремонт генератора Введение в тепломассообмен
Введение в тепломассообмен Механические колебания и их характеристики
Механические колебания и их характеристики Понятие о технической системе. 6 класс
Понятие о технической системе. 6 класс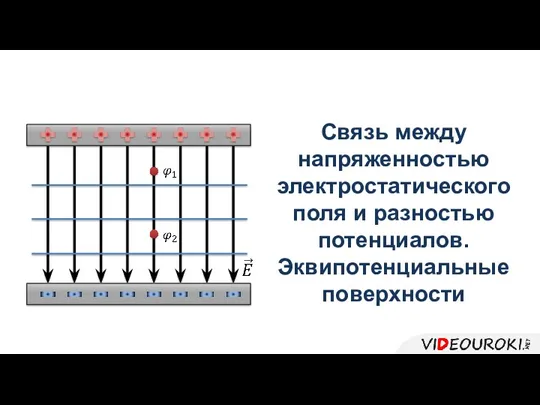 Связь между напряженностью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности
Связь между напряженностью электростатического поля и разностью потенциалов. Эквипотенциальные поверхности Понятие излучения. Поток излучения. Реактор как источник излучений. Первичные и вторичные источники излучений
Понятие излучения. Поток излучения. Реактор как источник излучений. Первичные и вторичные источники излучений Качество электроэнергии
Качество электроэнергии Колебания и волны
Колебания и волны Агрегатные состояние вещества (7 класс)
Агрегатные состояние вещества (7 класс) Жартылай өткізгішті фотодиодтар
Жартылай өткізгішті фотодиодтар Основні поняття та визначення з фізики
Основні поняття та визначення з фізики Электрический ток в вакууме. Диод
Электрический ток в вакууме. Диод Своя игра по физике
Своя игра по физике Treinamento de Televisores com LCD
Treinamento de Televisores com LCD