Основы теории напряженного состояния. Понятия главных площадок и главных напряжений. Лекция 9 презентация

Совокупность напряжений, возникающих во множестве площадок, проходящих через рассматриваемую точку, называется напряженным состоянием в точке. Для исследования напряженного состояния в окрестности произвольной точки тела выделяют элемент в виде бесконечно малого параллелепипеда.
Полное напряжение на его грани можно разложить на одно нормальное и два касательных напряжения.

Из условия равенства нулю суммы моментов всех сил относительно
осей x, y, z следует закон парности касательных напряжений.
На двух взаимно перпендикулярных площадках составляющие касательных напряжений,
перпендикулярные общему ребру, равны
и направлены либо к ребру, либо от ребра.

Напряженное состояние в точке можно характеризовать симметричным тензором второго ранга:

Если ориентацию граней выделенного элемента изменить, то будут изменяться как нормальные, так и касательные напряжения. При этом можно найти такие площадки, на которых касательные напряжения равны нулю. Такие площадки называются главными, а нормальные напряжения на этих площадках – главными напряжениями.
Все три выделенные площадки взаимно перпендикулярны.
В порядке убывания главные напряжения обозначают
σ1, σ2, σ3 (σ1> σ2 >σ3).

Переходя к тензорной форме записи, получим:

Если все три главных напряжения отличны от нуля, то напряженное состояние называют трехосным или объемным.
Трехосное напряженное состояние возникает в толстостенных сосудах.
При двух главных напряжениях, отличных от нуля, возникает двухосное,
или плоское, напряженное состояние. Плоское напряженное состояние возникает при поперечном изгибе, чистом сдвиге, кручении бруса (вала), а также при изгибе с кручением и в тонкостенных сосудах.
Если не равно нулю одно главное напряжение, то напряженное состояние называют одноосным или линейным.
Одноосное напряженное состояние возникает при растяжении (сжатии) стержней или при чистом изгибе.

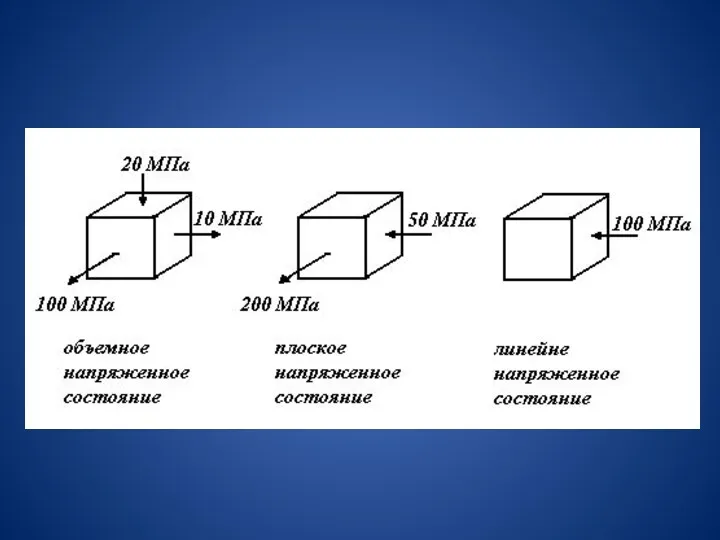
Для показанных элементов.
Трехосное напряженное состояние:
σ1 = 100 МПа, σ2 = 10 МПа, σ3 = - 20 МПа.
Двухосное, или плоское, напряженное состояние:
σ1 = 200 МПа, σ2 = 0, σ3 = - 50 Мпа.
Одноосное напряженное состояние:
σ1 = σ2 = 0, σ3 = - 100 МПа.

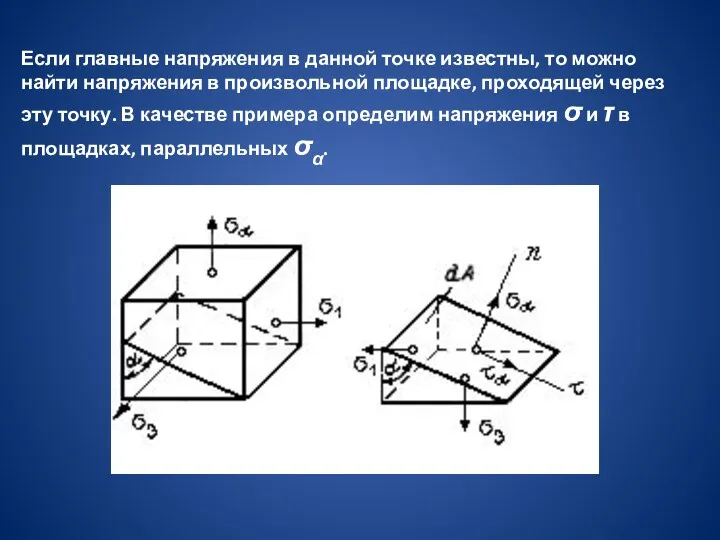
Если главные напряжения в данной точке известны, то можно найти напряжения в произвольной площадке, проходящей через эту точку. В качестве примера определим напряжения σ и τ в площадках, параллельных σα.

Проецируя все силы на направление нормали n, получим:
.
Проецируя все силы на направление касательной τ, получим:
.
Максимальные из всех возможных касательные напряжения:
.
Максимальные напряжения возникают на площадках, наклоненных под углом 45° к главным площадкам.

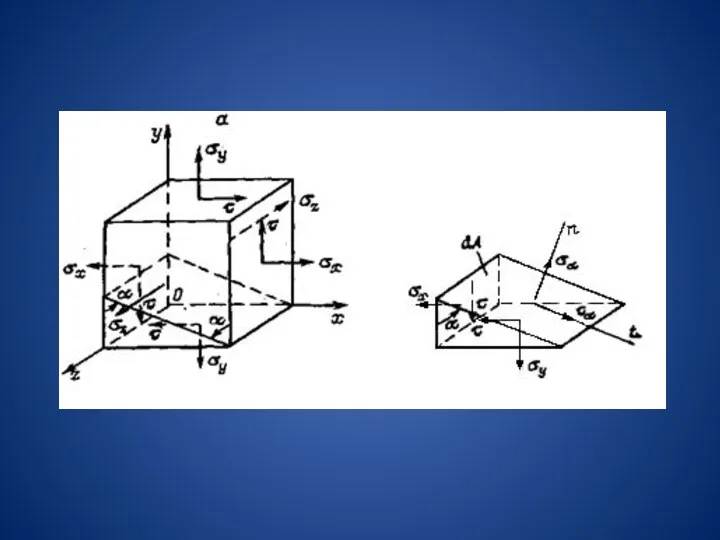
На практике чаще известны нормальные σx , σy , σz и касательные напряжения τ (τ = τxy = τyz ) на некоторых двух взаимно перпендикулярных площадках , а определить необходимо значение остальных двух главных напряжений и положение остальных двух главных площадок (σz— главное напряжение — известно).
Проецируя все силы на направление нормали n, получим:
.
Проецируя все силы на направление касательной τ, получим:
.
На главных площадках возникают экстремальные нормальные напряжения. Два значения угла α , отличающиеся на 90°, определяют положение этих площадок –
.

Подставив значения угла α :
,
.
В частном случае плоского напряженного состояния при σy = σz = 0
,
,
.

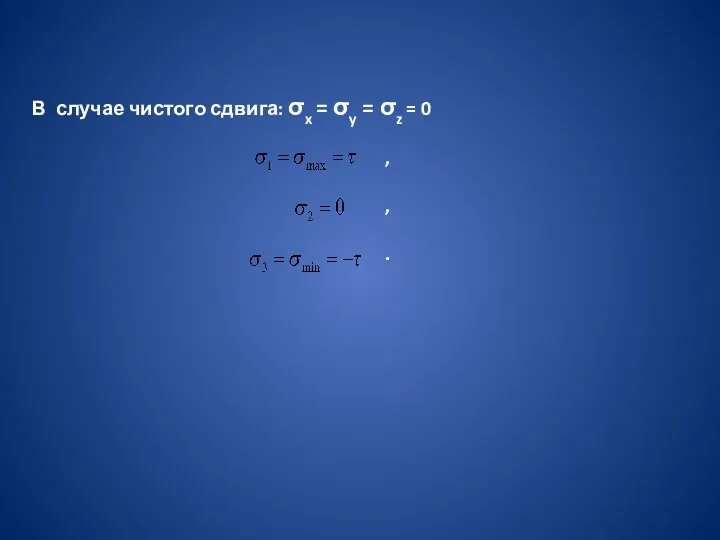
В случае чистого сдвига: σx = σy = σz = 0
,
,
.

Обобщенный закон Гука. Удельная потенциальная энергия. Понятие эквивалентного напряжения. Критерии прочности. Гипотезы прочности.

Обобщенный закон Гука
Обобщенный закон Гука для объемного (пространственного)
напряженного состояния имеет следующий вид:
ε1 = (σ1 – μ (σ2 + σ3))/ Е,
ε2 = (σ2 – μ (σ1 + σ3))/ Е,
ε3 = (σ3 – μ (σ1 + σ2))/ Е,
где μ – коэффициент Пуассона (коэффициент поперечной деформации).
Деформации ε1, ε2 и ε3 в направлении главных напряжений называются главными деформациями.

Коэффициент Пуассона μ не может быть больше 0,5.
Так как при трехосном растяжении объем элемента уменьшиться не может - значение относительного изменения объема ν
(ν = (V – Vо) / Vо = ε1 + ε2 + ε3 = (1 – 2 μ) (σ1 + σ2 + σ3)/Е)
должно быть положительно.
Это возможно лишь при условии 1 – 2 μ ≥ 0, так как главные напряжения в этом случае положительны (σ1 ≥ σ2 ≥ σ3 > 0).

При всестороннем равномерном сжатии σ1 = σ2 = σ3 = – р
ν = – р) / К ,
где К = Е/3(1-2μ).
Величину К называют модулем объемной деформации.

Удельная потенциальная энергия, накопленная в единице объема при действии главных напряжений σ1, σ2 и σ3 :
u = (σ1ε1 + σ2ε2 + σ3ε3)/2.
После подстановки значений σ1, σ2 и σ3 из обобщенного закона Гука:
u = (σ12 + σ22 + σ32 – 2 μ (σ1σ2+ σ2σ3+ σ3 σ1))/ 2Е.

Построение гипотез прочности основывается на предпосылке, состоящей в том, что два каких-либо напряженных состояния считаются равноопасными и равнопрочными, если они при пропорциональном увеличении главных напряжений в одно и то же число раз одновременно становятся предельными.
В этом случае коэффициент запаса прочности для обоих напряженных состояний при указанных условиях будет одинаковым.
Для заданного материала сравнение напряженных состояний можно производить по коэффициенту запаса n = nэкв.
Эквивалентным называют напряжение, которое нужно создать
в растянутом образце из того же материала, чтобы его напряженное
состояние стало равноопасно заданному объемному.

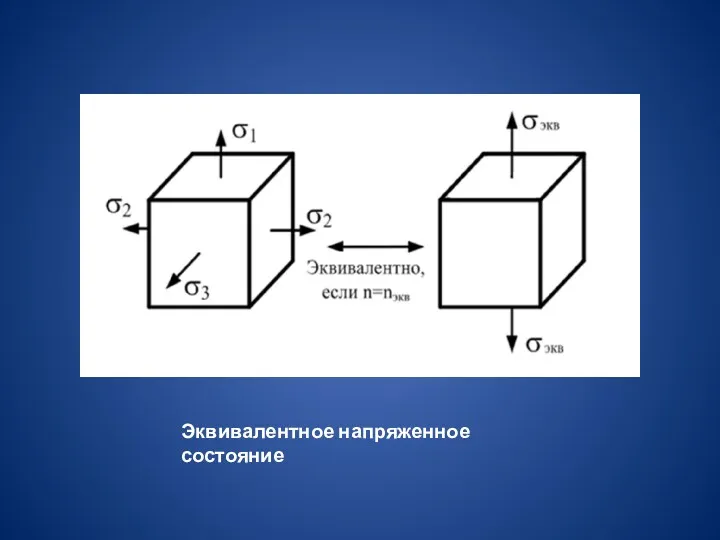
Эквивалентное напряженное состояние

Критерием прочности (критерием предельного напряженно-деформированного состояния) называют параметр (фактор), на основании которого производится оценка прочности и выявляется равноопасное состояние.
Опасность нагружения оценивают следующим образом:
- заменяют пространственное (сложное) напряженное состояние эквивалентным одноосным;
- сравнивают эквивалентное напряженное состояние с одноосным допускаемым напряженным состоянием.
Следовательно, задача сводится к нахождению эквивалентного напряжения. Величина этого напряжения зависит от методов расчета (гипотез прочности).

Первая (I) гипотеза прочности также называется гипотезой наибольших нормальных напряжений. Согласно этой гипотезе, выдвинутой Галилеем в XVII веке, преимущественное влияние на прочность оказывает величина наибольшего нормального напряжения, т.е. за критерий прочности принята величина наибольшего нормального напряжения.
Формулировка:
прочность материала при сложном напряженном состоянии обеспечивается, если наибольшее нормальное напряжение не превосходит допускаемого нормального напряжения, установленного для одноосного напряженного состояния.
Условие прочности:
σэквI = σ1 ≤ [σ]р ,
σэквI = σ3 ≤ [σ]с ,
где [σ]р, [σ]с – допускаемые напряжения на растяжение и сжатие.

Вторая (II) гипотеза прочности называется гипотезой наибольших
линейных деформаций. Согласно этой гипотезе, выдвинутой
Мариоттом в XVII веке и развитой Сен-Венаном в XIX веке, в качестве
критерия прочности принимают наибольшую по абсолютной величине
относительную линейную деформацию.
Формулировка:
прочность материала при сложном напряженном состоянии обеспечивается, если относительное наибольшее удлинение или укорочение в каком-либо направлении не превосходит величины, при которой происходит разрушение при простом растяжении или сжатии.
Условие прочности:
|ε|max ≤ [ε].
Допускаемая относительная деформация:
[ε] = [σ]/E,
где [σ] – допускаемое напряжение на растяжение или сжатие.

Чтобы не вычислять относительных деформаций, это условие прочности удобнее записать следующем образом:
σэкв = σ1 – μ (σ2 + σ3) ≤[σ],
σэкв = σ2 – μ (σ1 + σ3) ≤[σ],
σэкв = σ3 – μ (σ1 + σ2) ≤[σ].

Третья (III) гипотеза прочности – гипотеза наибольших касательных напряжений. В основе этой теории прочности лежит предположение, что основной причиной появления опасного состояния (текучести) материала являются наибольшие касательные напряжения.
Формулировка:
прочность материала при сложном напряженном состоянии обеспечивается, если максимальное касательное напряжение не превосходит допускаемого касательного напряжения при простом одноосном растяжении.
Условие прочности:
τmax ≤ [τ].

В случае объемного напряженного состояния максимальные касательные
напряжения –
τmax = (σ1 - σ3)/2.
В случае одноосного растяжения –
τmax = σэкв /2 и [τ] = [σ]/2.
Тогда
σэквIII = σ1 – σ3 ≤ [σ].

Теория прочности, обобщающая III гипотезу прочности и на случаи,
когда [σ]р ≠ [σ]с, носит название гипотезы прочности Мора
(критерий Мора) и имеет вид:
σэкв = σ1 – κσ3 ≤ [σ]р,
где [σ]р – допускаемое напряжение при одноосном растяжении;
κ = σтр / σтс для пластичных материалов и κ = σвр / σвс для хрупких материалов; σтр и σвр – предел текучести и предел прочности при растяжении, σтс и σвс – при сжатии.

Четвертая (IV) гипотеза прочности – гипотеза удельной потенциальной энергии формоизменения. Также она называется энергетической гипотезой прочности или гипотезой Губера-Мизеса.
В качестве критерия прочности принимается не вся энергия деформации, а лишь та ее часть, которая связана с изменением формы тела.
Формулировка:
прочность материала при сложном напряженном состоянии обеспечивается, если удельная потенциальная энергия формоизменения не превосходит допускаемой удельной потенциальной энергии, установленной для одноосного напряженного состояния.
Условие прочности:
uф≤ [uф]р.

Так как объем тела не меняется при значении коэффициента Пуассона
μ = 0,5, то удельную потенциальную энергию формоизменения можно записать в следующем виде:
uф = (σ12 + σ22 + σ32 – σ1σ2 – σ2σ3 – σ3 σ1)/2Е.
Допускаемая удельная потенциальная энергия при одноосном напряженном состоянии –
[uф]р = [σ]2/2Е.
Окончательно
σэквIV = (σ12 + σ22 + σ32 – σ1σ2 – σ2σ3 – σ3 σ1)1/2 ≤ [σ].

Тонкостенные оболочки. Основные допущения. Уравнение Лапласа.

Под оболочкой понимают тело, одно из измерений которого (толщина) значительно меньше двух других.
Геометрическое место точек, равноотстоящих от обеих поверхностей оболочки, называют срединной поверхностью.
Если срединная поверхность представляет собой поверхность вращения, такие оболочки называют осесимметричными.
Толщину оболочки принимают постоянной.
Полагают, что нагрузка также обладает свойствами осевой симметрии. (Для таких оболочек задача расчета существенно упрощается, так как все внутренние силы и напряжения зависят от текущего радиуса.)
В осесимметричных оболочках при осесимметричной нагрузке касательные напряжения отсутствуют.

Оболочку считают тонкостенной, если толщина стенки оболочки s диаметром D (кроме конической) удовлетворяет условию:
при D » 200 мм ,
при D < 200 мм ,
где С – поправка на коррозию.
В противном случае оболочку считают толстостенной.

Для тонкостенных оболочек можно принять, что нормальные напряжения равномерно распределены по толщине, то есть отсутствует изгиб оболочки. Теория оболочек, построенная в этом предположении, называется безмоментной теорией оболочек.
При отсутствии резких изменений формы оболочки, жестких защемлений, внешних сосредоточенных сил и моментов, можно с успехом применять к расчету оболочек на прочность безмоментную теорию. Если же имеются перечисленные особенности, то в местах крепления оболочки и резких изменений формы возникают дополнительные напряжения, связанные с изгибом оболочки. Решение подобных задач точными методами показывает, что зона изгибных напряжений весьма ограничена, и, поэтому на некотором удалении от перечисленных особых областей определение напряжений можно производить по безмоментной теории.

Рассмотрим осесимметричную тонкостенную оболочку толщиной s.
Обозначим:
- меридиональный радиус
(радиус кривизны дуги меридиана срединной поверхности),
- окружной радиус
(этот радиус равен отрезку нормали между срединной
поверхностью и осью симметрии).
Действие отброшенной части оболочки заменим:
- меридиональным напряжением,
- окружным (или тангенциальным) напряжением.
Нагрузка на элемент – внутреннее избыточное давление р.

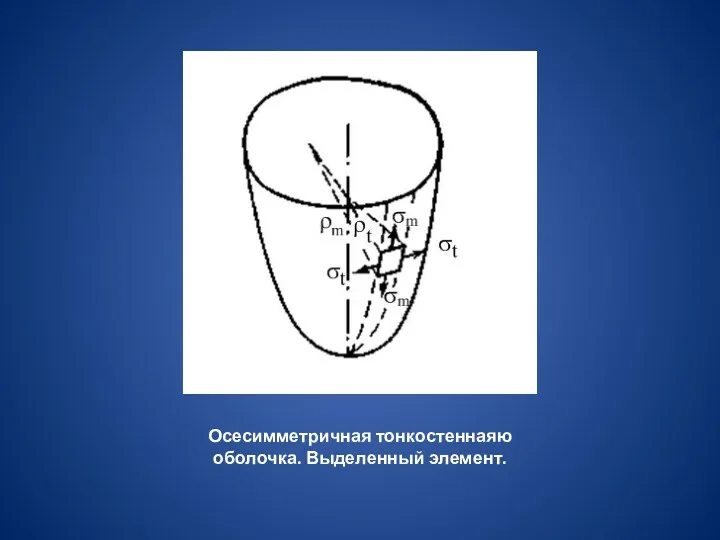
Осесимметричная тонкостеннаяю оболочка. Выделенный элемент.

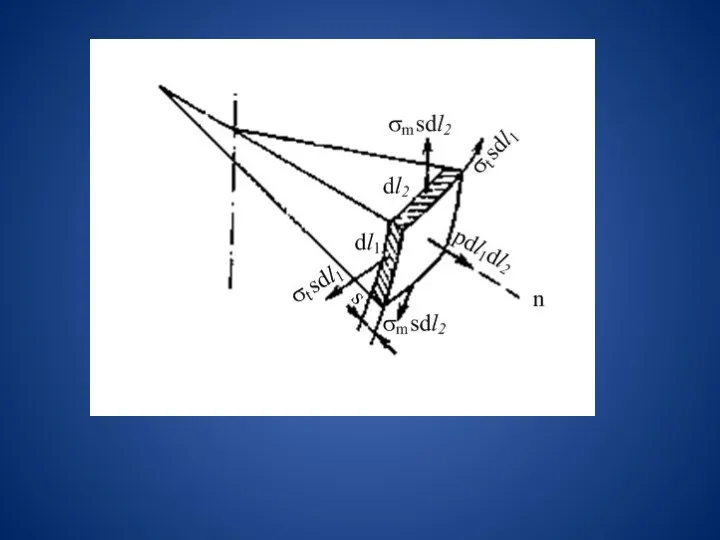
Пояснение к чертежу:
р - внутреннее избыточное давление,
- сила давления ,
, - силы, перпендикулярные к соответствующим граням
выделенного элемента,
n - нормаль.

Уравнение Лапласа:
.
( Уравнение получено путем проектирования всех сил на направление нормали).
Второе уравнение для определения напряжений и можно получить, спроектировав все силы на направление оси оболочки. Однако это удобнее делать не для выделенного элемента, а для отсеченной части конкретной оболочки.
Если оболочка подвержена воздействию наружного избыточного давления, то формально уравнение Лапласа остается справедливым, если изменить знак давления. Однако в стенках оболочки при этом возникнут сжимающие напряжения, что может привести к потере устойчивости (формы) оболочки.

Напряжения и являются главными напряжениями. Третье главное напряжение – радиальное напряжение . На внутренней поверхности оболочки радиальное напряжение равно , а на наружной – нулю.
В тонкостенных оболочках и всегда значительно больше (примерно в 50 ÷ 100 раз). Поэтому величиной радиального напряжения пренебрегают ( ) и напряженное состояние тонкостенной оболочки считается двухосным.

Сферический сосуд под действием
внутреннего газового давления Pг .
В этом случае вследствие центральной симметрии
, .
Поэтому .
Главные напряжения: , .
По III и IV гипотезам прочности: ,
где R – радиус срединной поверхности R ≈ D/2 (D – внутренний диаметр сосуда).