Содержание
- 2. ЗОННАЯ ТЕОРИЯ ТВЕРДОГО ТЕЛА Энергетический спектр электрона в изолированном атоме представляет собой ряд тонких линий, разделенных
- 3. ЗОННАЯ ТЕОРИЯ ТВЕРДОГО ТЕЛА При объединении атомов в кристалл значение энергии атома изменяется по отношению к
- 4. Трансляционная симметрия в кристаллах Важные свойства электрона, позволяющие построить теорию электронных состояний: Квантовые частицы неотличимы Вероятностный
- 5. «Потенциальная яма»
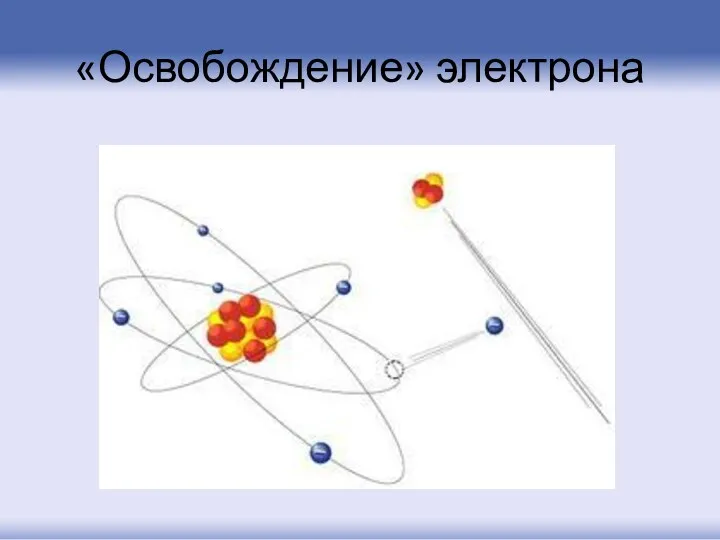
- 6. Под влиянием внешних факторов (света, температуры и т.д.) электрон может увеличить свою кинетическую энергию и перейти
- 7. «Освобождение» электрона
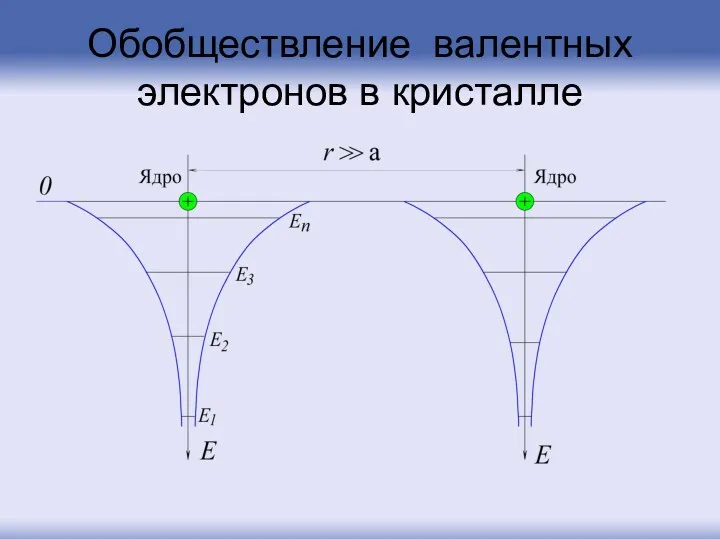
- 8. При сближении атомов потенциальные кривые частично налагаются друг на друга и дают результирующий потенциальный рельеф с
- 9. Обобществление валентных электронов в кристалле
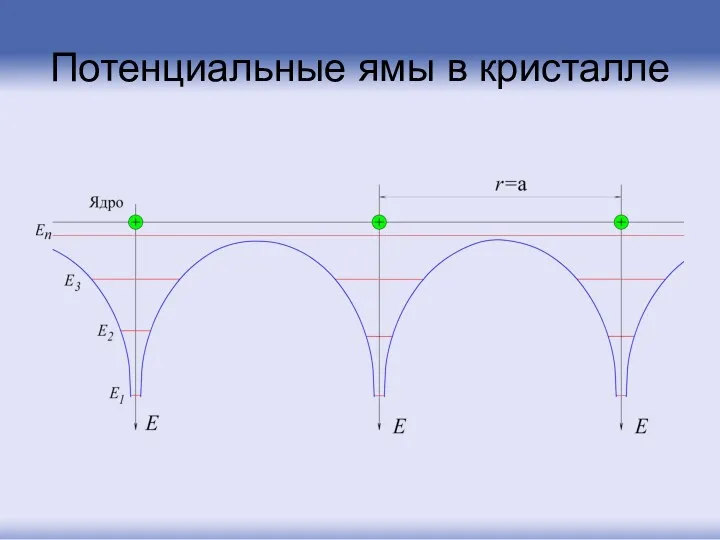
- 10. Потенциальные ямы в кристалле
- 11. До тех пор, пока электрон будет находиться в кристалле, он будет не совсем свободен, то есть
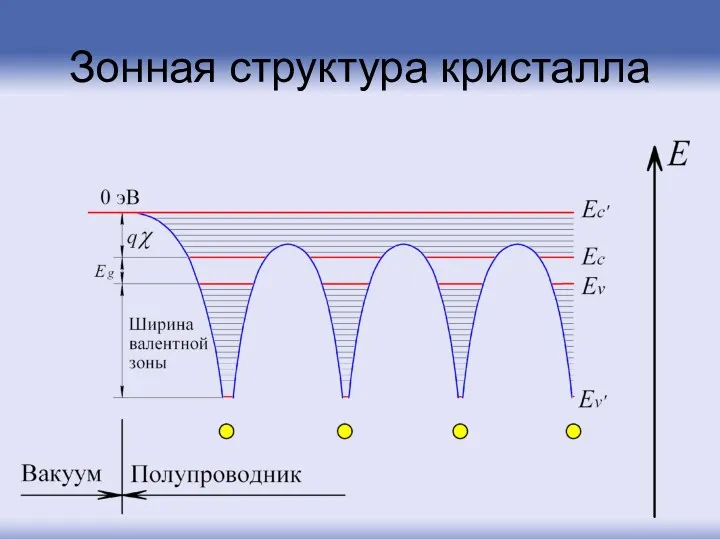
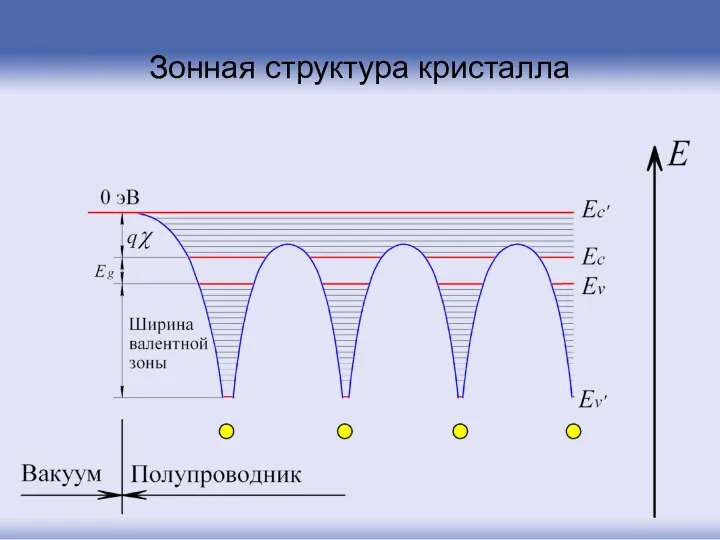
- 12. Зонная структура кристалла
- 13. свободный электронный газ Для металлов и полупроводников вводят понятие свободный электронный газ (3D-газ). Электронный газ –
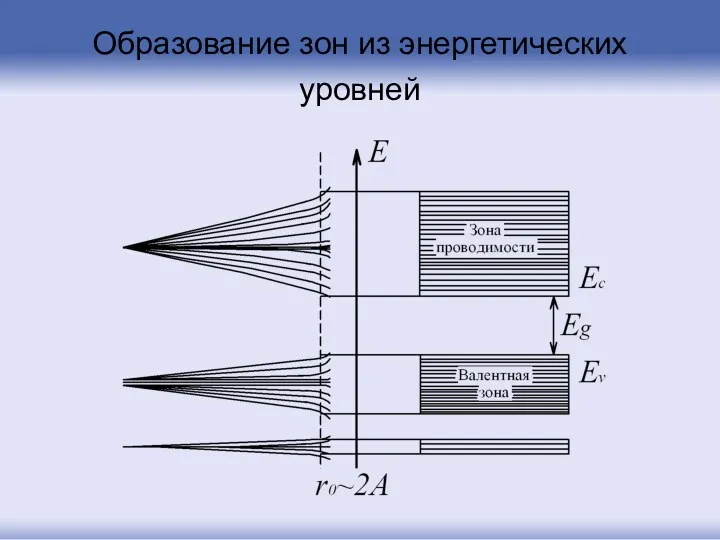
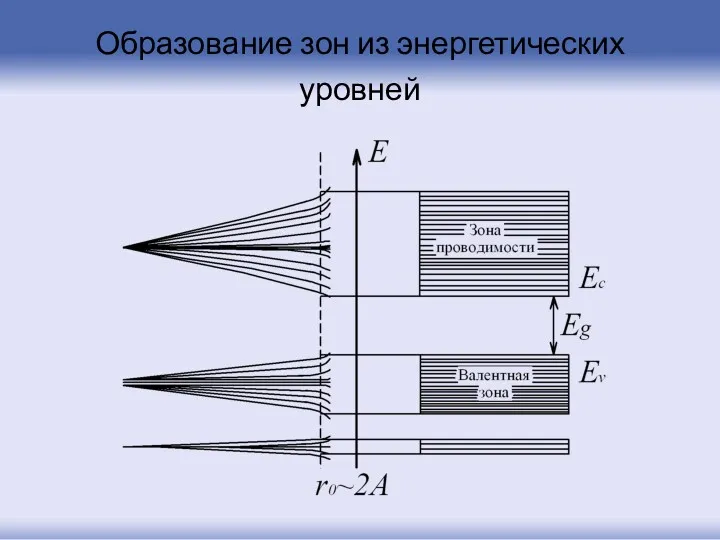
- 14. Образование зон из энергетических уровней
- 15. Зонная структура кристалла
- 16. Потенциальная энергия электрона где (x, y, z) – радиус-вектор данной точки пространства, – вектор кристаллической решетки
- 17. Граничные условия Борна – Кармана Периодическое (циклическое) изменение потенциальной энергии накладывает ограничения на периодическую волновую функцию
- 18. где i принимает значения, соответствующие размерности решетки Бравэ, – вектор элементарной трансляции, Ni – любое целое
- 19. Уравнение Шредингера для частицы (электрона) в периодической решетке:
- 20. Браве (Bravais) Огюст (1811—1863)
- 21. Что такое решетка Бравэ? Решетка Браве (названа в честь французского физика Огюста БравеРешетка Браве (названа в
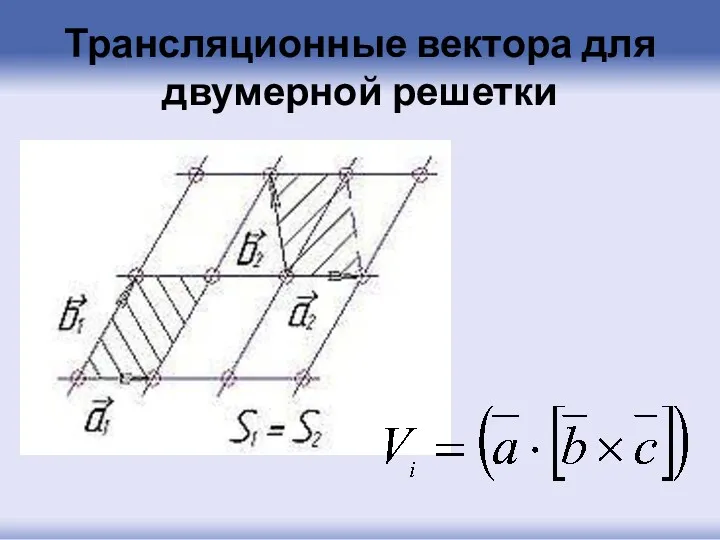
- 22. Трансляционные вектора для двумерной решетки
- 23. Решеткой или системой трансляций Браве называется набор элементарных трансляций или трансляционная группа, которыми может быть получена
- 24. Элементарная ячейка решетки Браве – параллелепипед, построенный на основных векторах трансляции. В трехмерном случае таких некомпланарных
- 25. Основным трансляционным вектором называется минимальный в данном направлении вектор перехода из данной точки в ближайшую эквивалентную.
- 26. Элементарные ячейки, содержащие частицы только в вершинах, называют простыми, или примитивными. На каждую такую ячейку приходится
- 27. Базисом ячейки называют совокупность координат узлов, приходящихся на элементарную ячейку. Так в кремния (Si) в состав
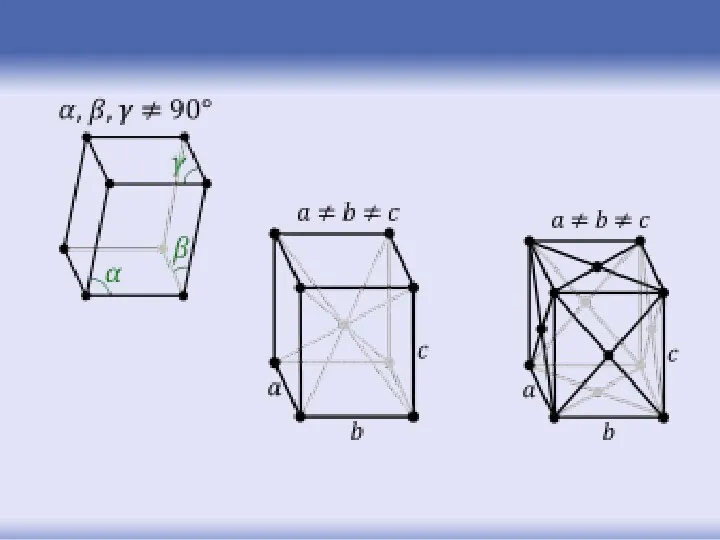
- 28. Типы решеток Браве Четырнадцать трехмерных решеток Браве обычно подразделяются на семь кристаллографических классов (сингоний), в соответствии
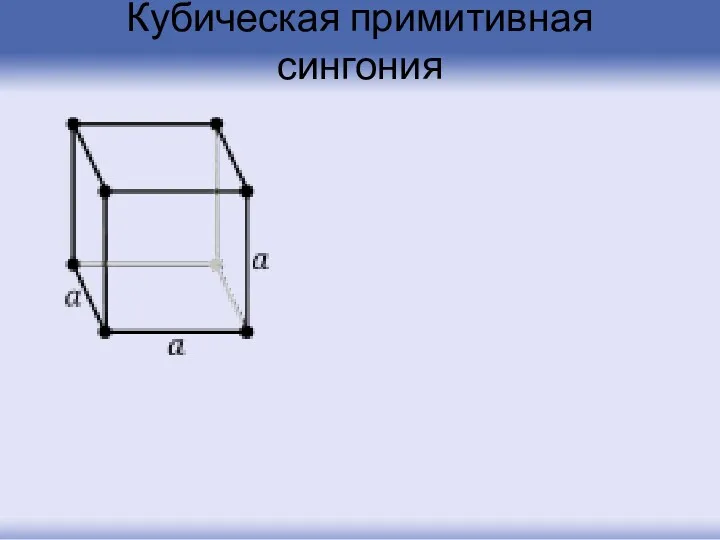
- 29. Кубическая примитивная сингония
- 31. кристаллографические плоскости и индексы Миллера Через узлы решетки можно провести ряд параллельных между собой узловых плоскостей.
- 32. Индексы Миллера Пусть одна из плоскостей отсекает на осях координат отрезки А, В и С. В
- 33. Индексы Миллера
- 34. Индексы Миллера Целые числа h, k, l, обратно пропорциональные отрезкам, которые отсекают плоскость на координатных осях,
- 35. Индексы Миллера Индексы Миллера находятся следующим образом: Определяются координаты (х, у, z) пересечения плоскости с кристаллографичискими
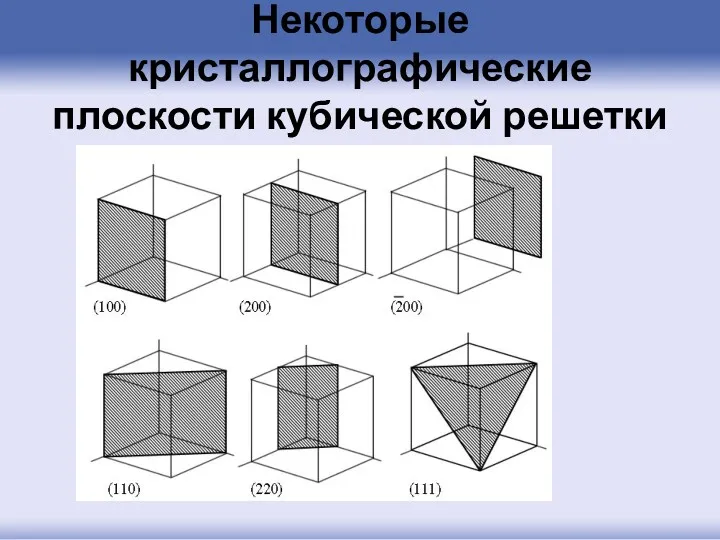
- 36. Некоторые кристаллографические плоскости кубической решетки
- 37. Заметим, что параллельно изображенной плоскости можно провести много параллельных плоскостей, проходящих через узлы кристаллической решетки, откладывая
- 38. По аналогии с прямой кристаллической решеткой можно построить обратную решетку, широко используемую в рентгеновской кристаллографии и
- 39. координатные оси и единичные вектора выбираются следующим образом т.е. чтобы скалярное произведение одноименных векторов равнялось бы
- 40. Вектор перпендикулярен векторам и∙ следовательно, является нормалью к плоскости, в которой лежат эти вектора. Аналогично вектора
- 41. Теорема Блоха Рассмотрим идеальный бесконечный кристалл, т.е. кристалл, в котором отсутствуют дефекты, и который обладает трансляционной
- 42. Феликс Блох лауреат Нобелевской премии по физике
- 43. Теорема Блоха устанавливает вид волновой функции частицы, находящейся в периодическом потенциале В этом случае гамильтониан для
- 44. – периодическое поле кристаллической решетки по всем векторам r решетки Бравэ, могут быть выбраны таким образом,
- 45. В иной записи теорема Блоха имеет вид Согласно теореме БлохаСогласно теореме Блоха, в таком виде можно
- 46. Соответствующие им собственные значения энергии En( )=En( + n) периодичны по векторам обратной решетки. Поскольку уровни
- 47. Так как собственные значения энергии при заданном n, периодичны по , то волновой вектор может быть
- 48. Иными словами, обладает свойством трехмерной периодичности кристалла. Такую функцию можно разложить в ряд Фурье:
- 49. Действительная часть комплексной экспоненты где N – целое число Разрешенные значения – это любые волновые вектора,
- 50. Плоская волна удовлетворяет условиям Борна – Кармана только при ''разрешенных'' волновых векторах
- 51. Иными словами, на длине L должно укладываться целое число длин волн: λ = L/N. Следовательно, волновые
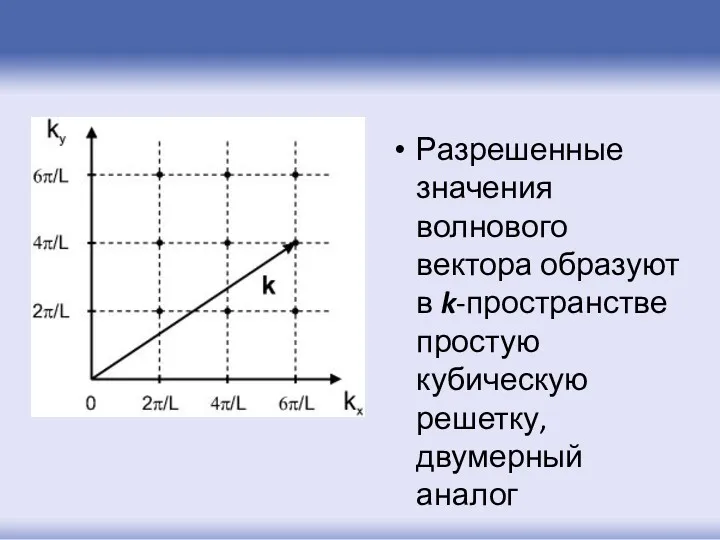
- 52. Разрешенные значения волнового вектора образуют в k-пространстве простую кубическую решетку, двумерный аналог
- 53. Рассмотрим идеальный бесконечный кристалл, т.е. кристалл, в котором отсутствуют дефекты, и который обладает трансляционной симметрией. При
- 54. В элементе объема обратного пространства Δ3k содержится разрешенных состояний. Соответственно, – число состояний в элементе Δ3k,
- 55. Вектор определяет узлы обратной решетки
- 56. Используя определение векторов , , , можно найти объем ячейки обратной решетки: Вектор определяет узлы обратной
- 57. Из трансляционного условия, накладываемого на волновую функцию электрона, движущегося в поле кристалла следует, что и для
- 58. Таким образом, уравнение Шредингера для свободной частицы имеет вид и решение в виде плоских волн де-Бройля
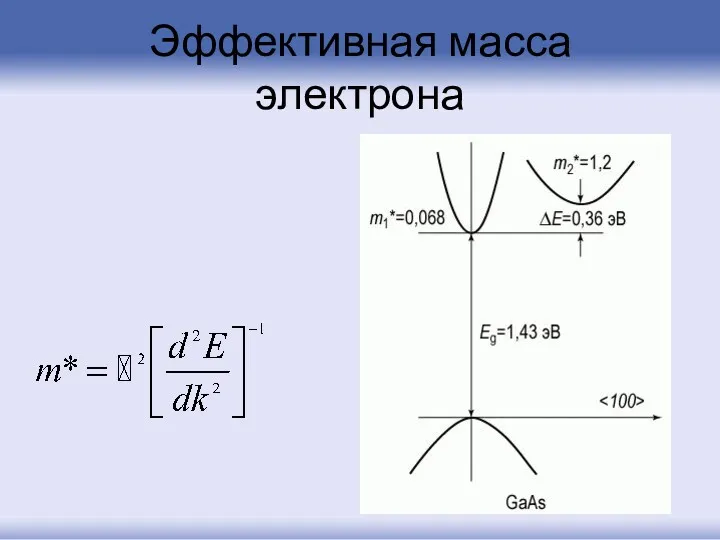
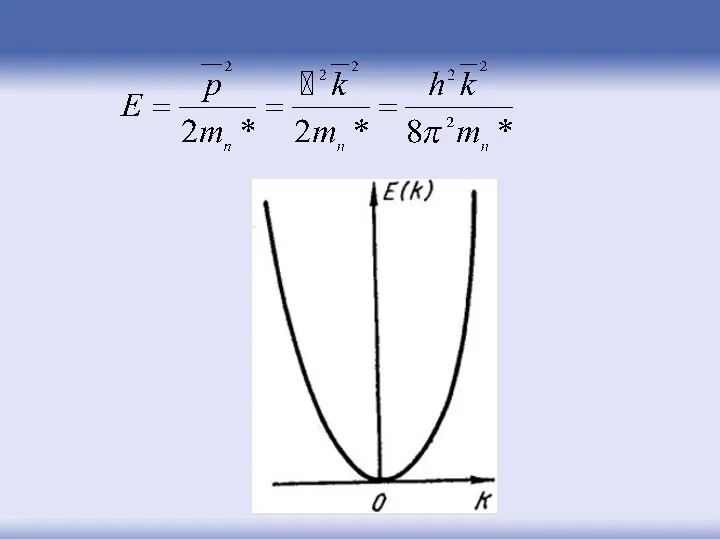
- 59. Эффективная масса электрона
- 60. Зоны Бриллюэна Пространство (или ) можно разбить на области физически эквивалентных состояний, называемые зонами Бриллюэна Первой,
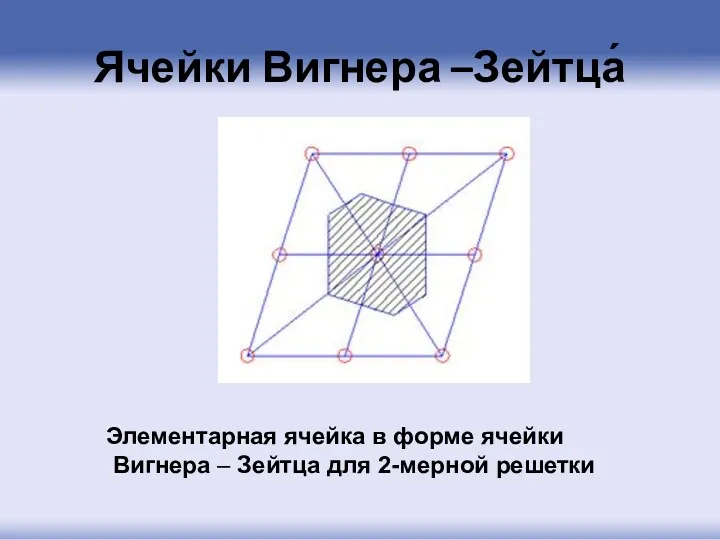
- 61. Ячейки Вигнера –Зейтца́ Элементарная ячейка в форме ячейки Вигнера – Зейтца для 2-мерной решетки
- 62. Ячейка Вингера –Зейтца это примитивная ячейка (содержит только один узел решетки), обладающая полной симметрией решетки Браве
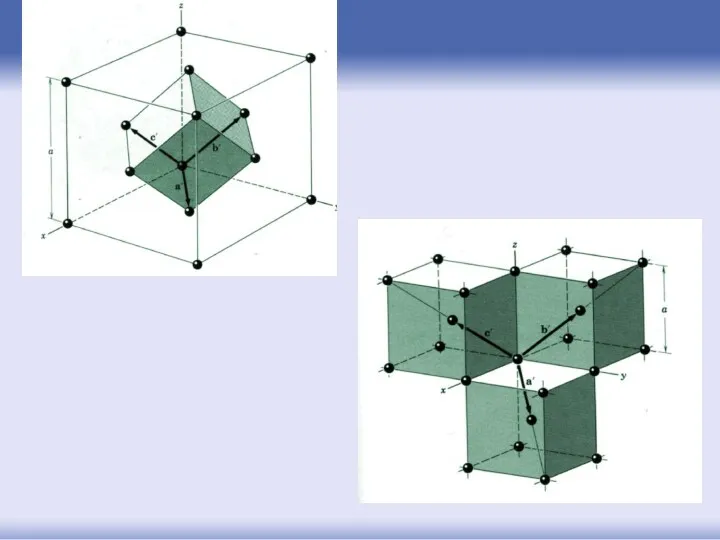
- 63. Принцип построения зон Бриллюэна
- 64. Объем всех зон Бриллюэна одинаков и равен объему примитивной ячейки обратной решетки Любой процесс в расширенной
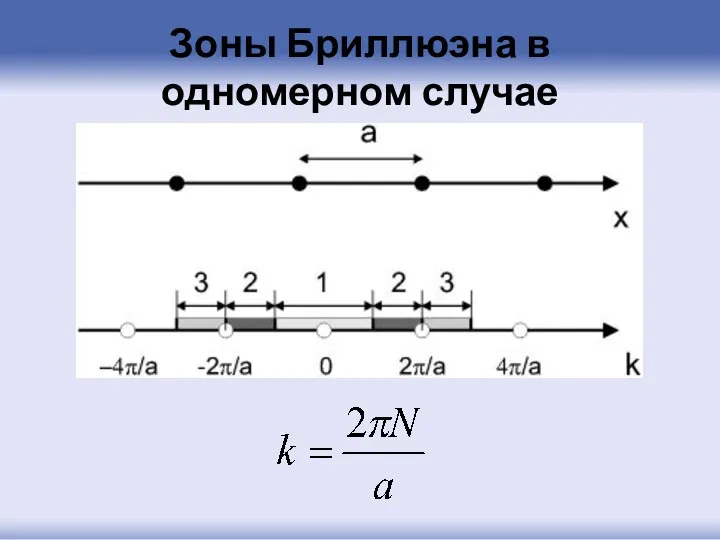
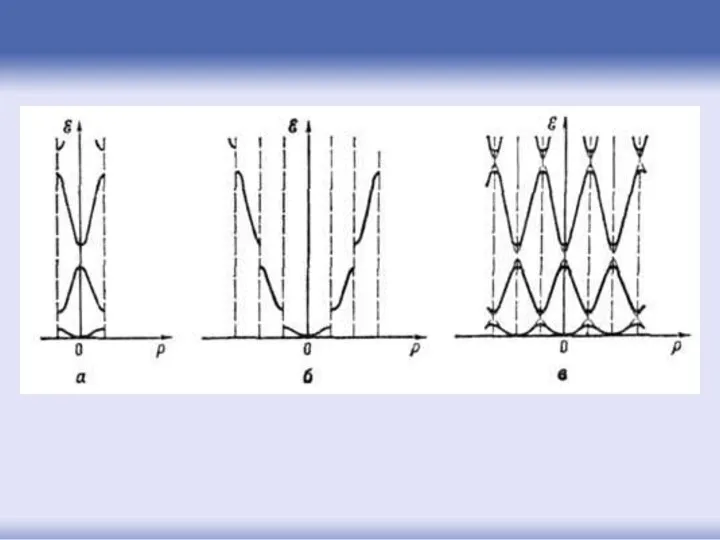
- 65. Зоны Бриллюэна в одномерном случае
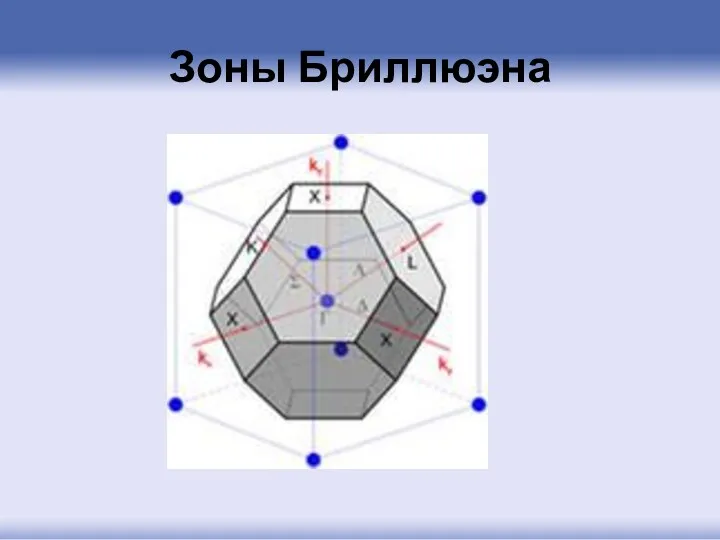
- 66. Зоны Бриллюэна
- 68. Для кристалла с простой кубической решеткой зона Бриллюэна в -пространстве представляет собой куб объемом .
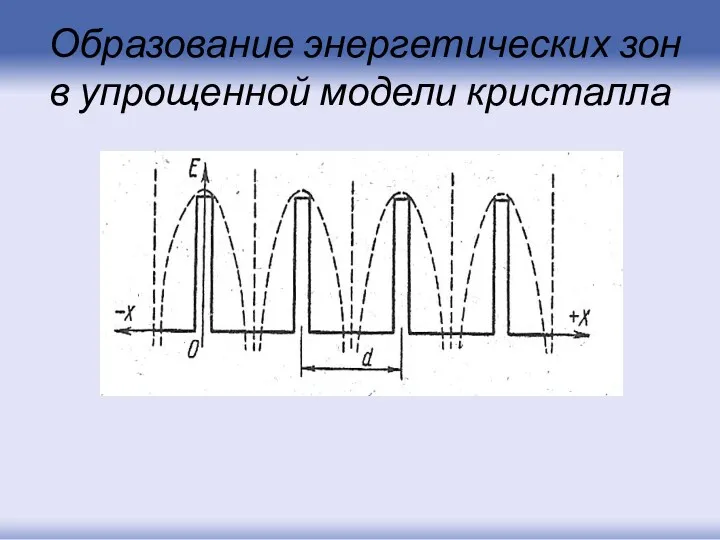
- 69. Образование энергетических зон в упрощенной модели кристалла
- 70. Если электрон заперт в атоме, кристалле или любой потенциальной яме, то в соответствие с граничными условиями
- 71. Предположив, что решение имеет вид т. е. что волновая функция зависит от времени через экспоненциальный множитель
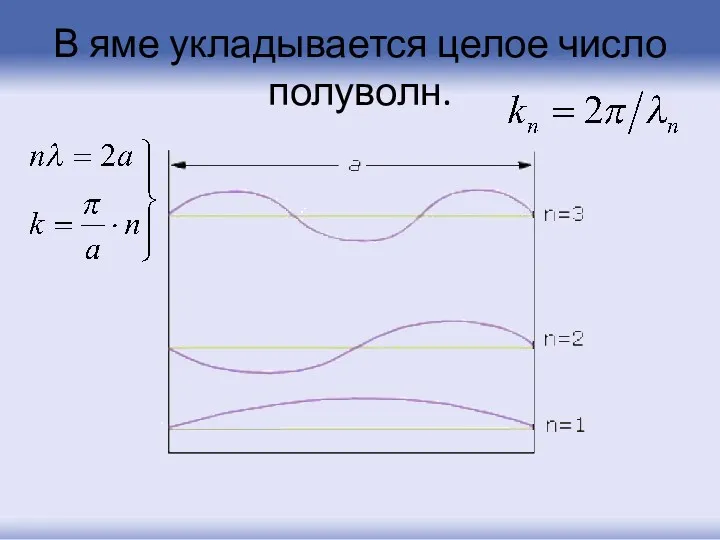
- 72. В яме укладывается целое число полуволн.
- 73. Волновую функцию такого электрона можно представит в следующем виде: , где n=2, 4, 8... – четный
- 74. Каждому уровню энергии Е1, Е2 ,… Еп соответствует своя стоячая электронная волна, электрон колеблется вокруг и
- 75. Когда волновой вектор становится равным , все отраженные волны оказываются в фазе (условие брегговского отражения), и
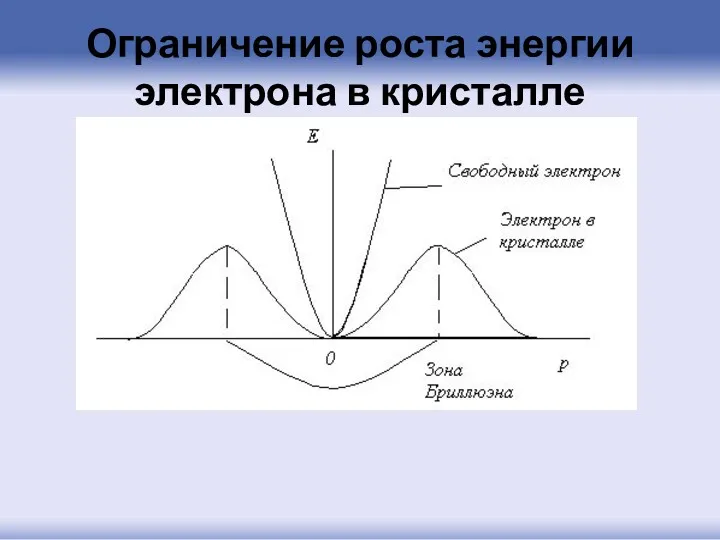
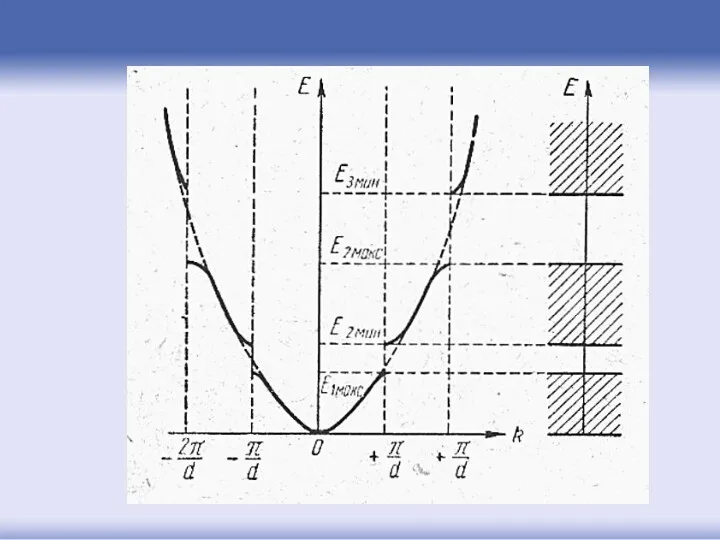
- 77. Ограничение роста энергии электрона в кристалле
- 78. Вблизи нулевых значений импульса (волнового вектора) зависимость энергии очень мало отличается от параболы, но вдали от
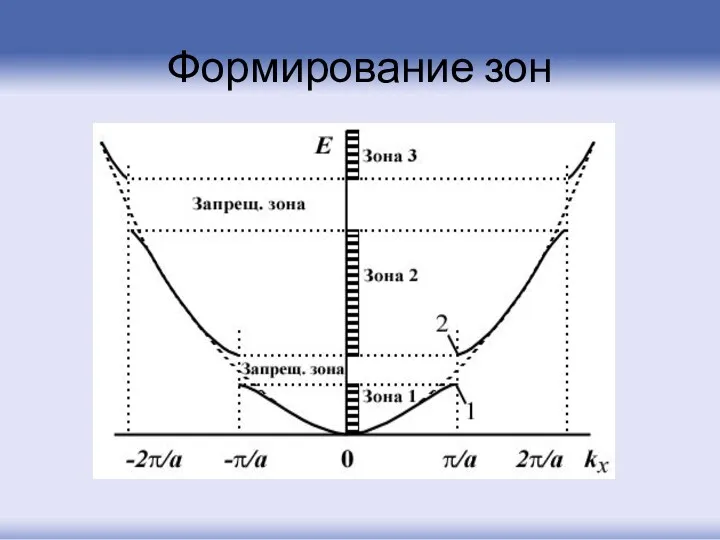
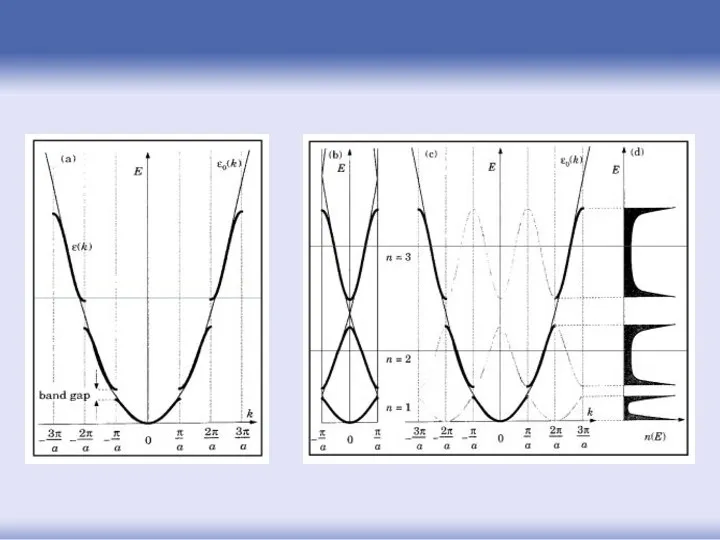
- 80. Формирование зон
- 81. Соответственно разделению -пространства на зоны Бриллюэна, энергетический спектр электронов разделен на энергетические зоны: 1-й зоне Бриллюэна
- 84. Таким образом, о зонах Бриллюэна говорим, когда имеем дело с -пространством, об энергетических зонах, когда анализируем
- 85. Образование зон из энергетических уровней
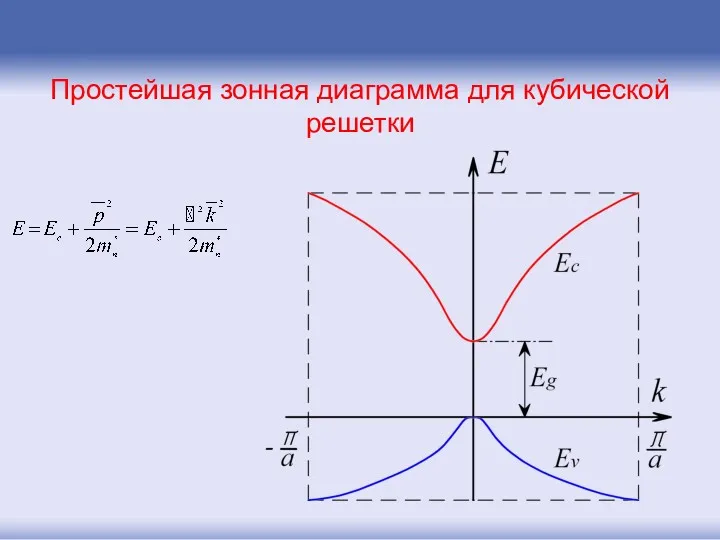
- 86. Простейшая зонная диаграмма для кубической решетки
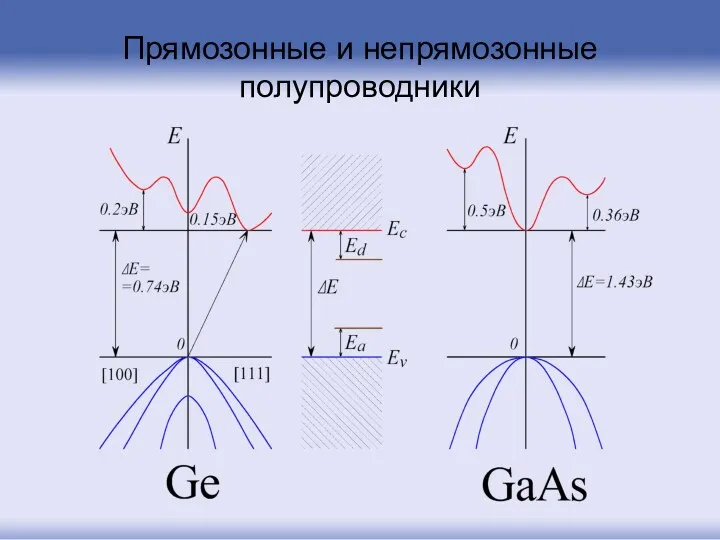
- 87. Прямозонные и непрямозонные полупроводники
- 88. Классификация веществ по ширине запрещенной зоны
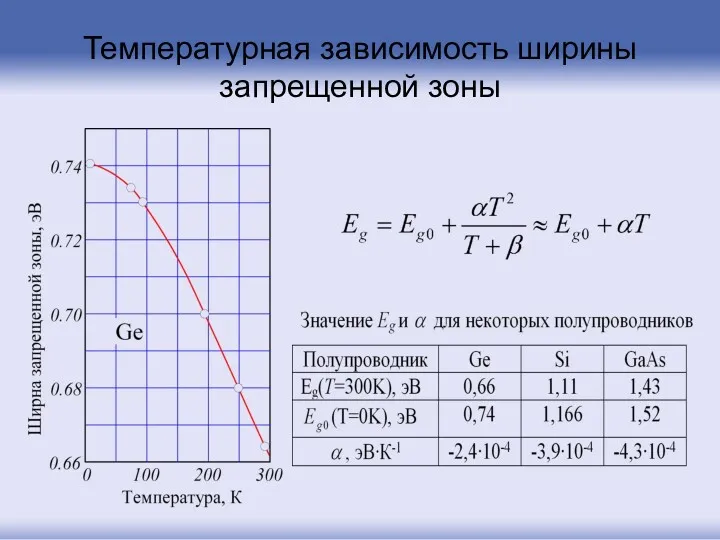
- 89. Температурная зависимость ширины запрещенной зоны
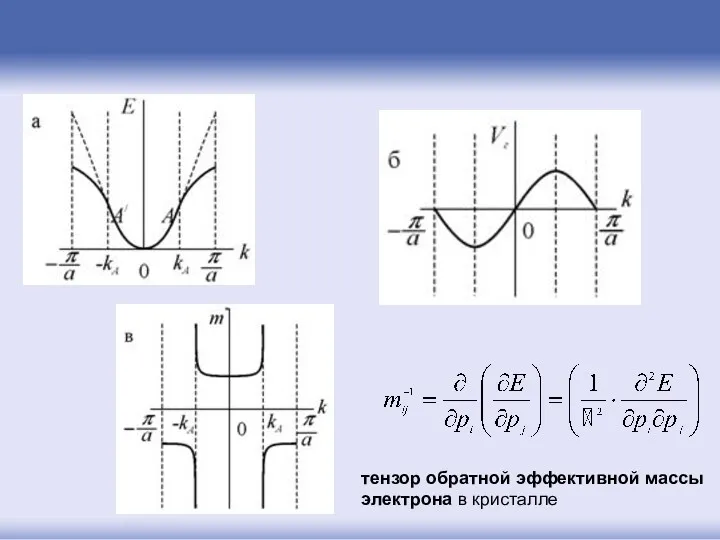
- 90. тензор обратной эффективной массы электрона в кристалле
- 91. Зависимость энергии от квазиимпульса в InSb
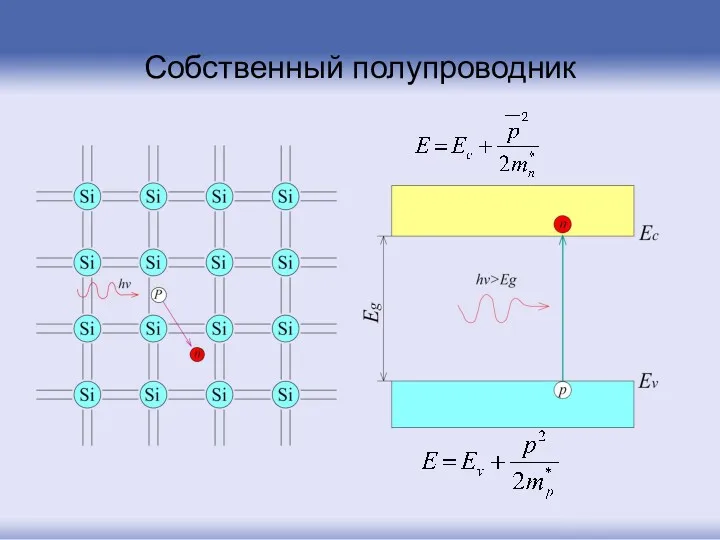
- 93. Собственный полупроводник
- 94. Собственный полупроводник
- 95. Собственный полупроводник Энергия, необходимая для увеличения концентрации носителей на единицу, называется энергией Ферми. Для чистого (беспримесного,
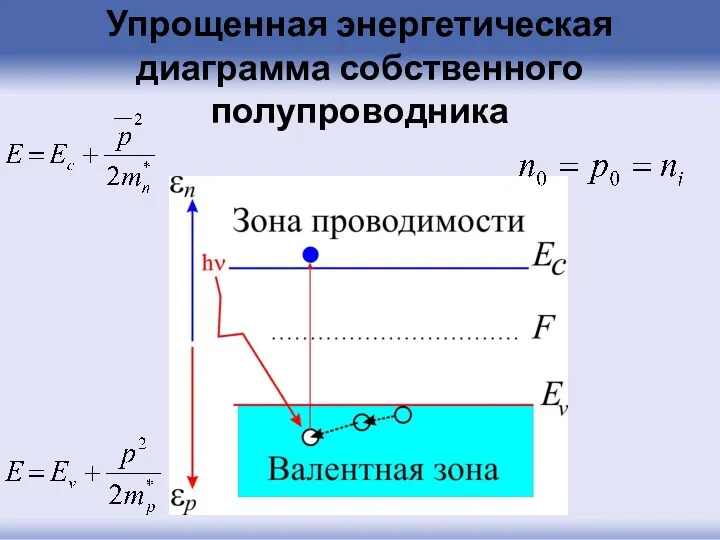
- 96. Упрощенная энергетическая диаграмма собственного полупроводника
- 97. Собственный полупроводник Концентрации носителей, находящихся в термодинамическом равновесии, равны между собой и равны собственной концентрации.
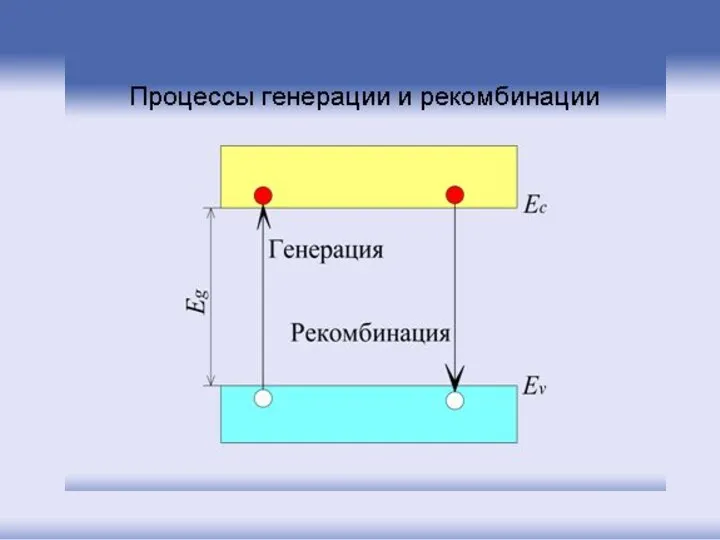
- 98. Собственный полупроводник Образовавшиеся в результате разрыва ковалентной связи (генерации) электрон и дырка хаотично передвигаются по кристаллу
- 99. Реальные кристаллы Реальные кристаллы несовершенны. Большинство кристаллов состоят из множества случайно ориентированных кристаллитов, отделенных друг от
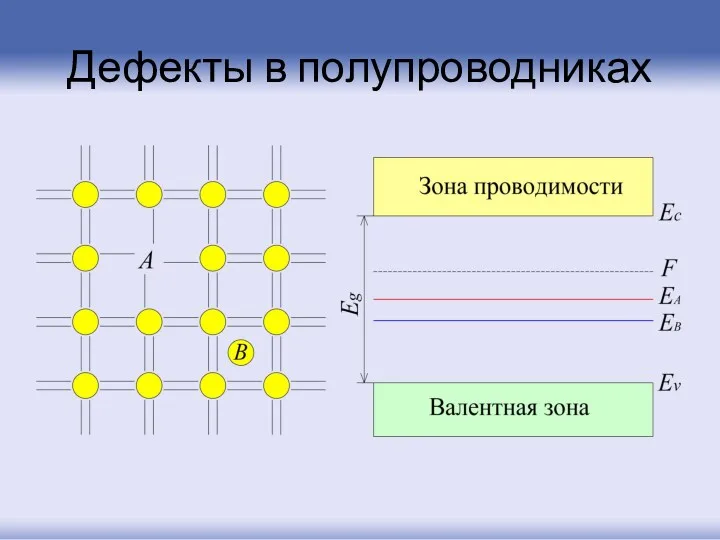
- 100. Дефекты в полупроводниках Наличие в кристалле дефектов приводит к появлению в запрещенной зоне энергетических уровней, положение
- 101. Дефекты в полупроводниках
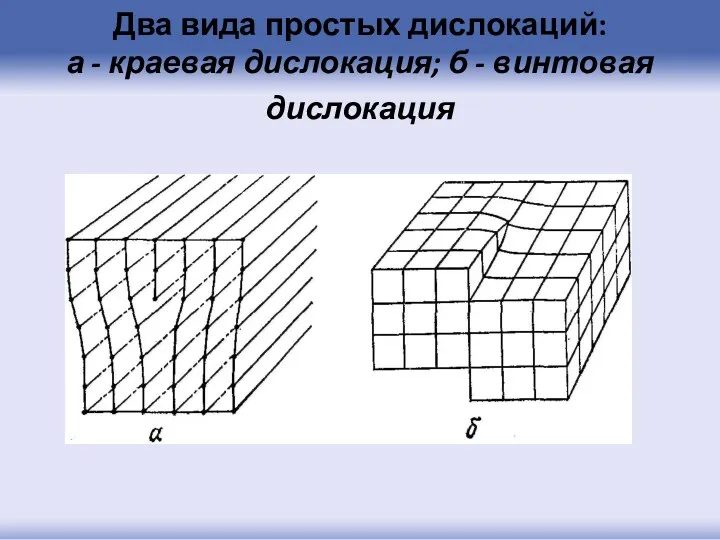
- 102. Два вида простых дислокаций: а - краевая дислокация; б - винтовая дислокация
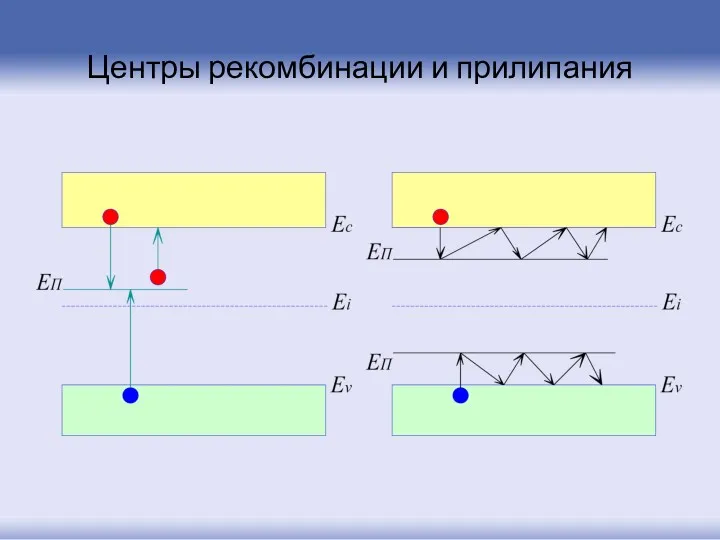
- 103. Центры рекомбинации и прилипания
- 104. Влияние поверхностных состояний на спектр энергетических уровней
- 105. Уравнение электронейтральности Для собственного полупроводника можно записать уравнение электронейтральности
- 106. Задача статистики – определение концентрации «свободных», то есть участвующих в электропроводности электронов и дырок. Пусть при
- 107. Допустим, имеется электронная система, в которой распределение энергетических уровней описывается функцией, зависящей от энергии N(E). Имеется
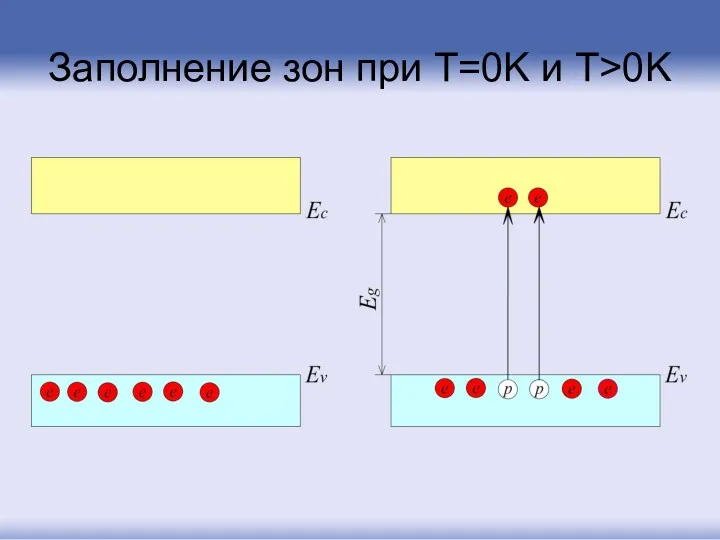
- 109. Заполнение зон при T=0K и T>0K
- 110. Вероятность заполнения энергетического уровня для частицы с полуцелым спином (фермиона), то есть вероятность нахождения электрона на
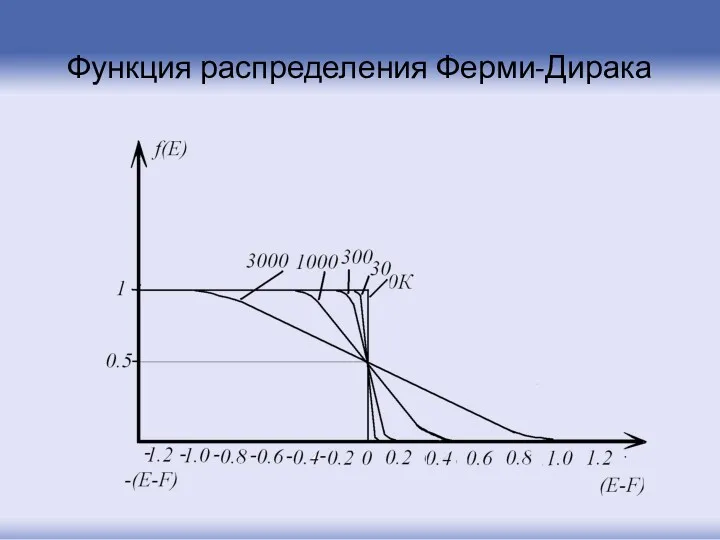
- 111. Функция распределения Ферми-Дирака
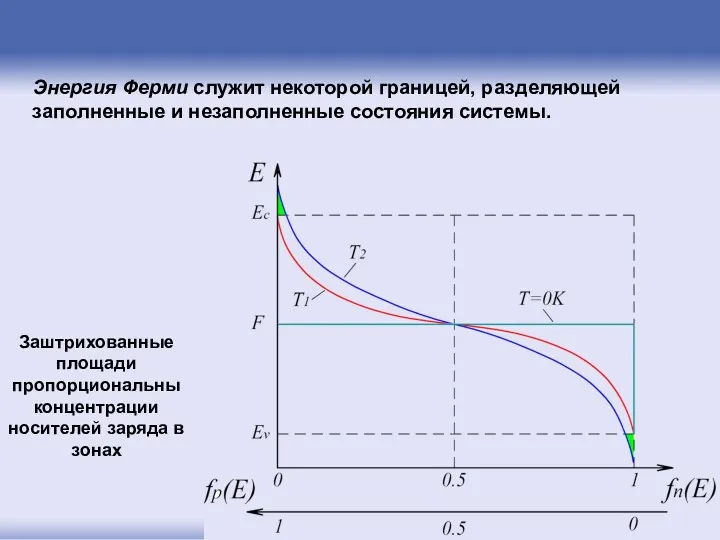
- 112. Энергия Ферми служит некоторой границей, разделяющей заполненные и незаполненные состояния системы. Заштрихованные площади пропорциональны концентрации носителей
- 113. Чтобы определить, какое число электронов в системе может принимать участие в электропроводности, необходимо рассчитать распределение концентрации
- 114. Заполнение электронами и дырками зон невырожденного полупроводника В невырожденном полупроводнике уровень Ферми находится между зоной проводимости
- 115. Статистика Максвелла-Больцмана и Ферми-Дирака
- 116. Больцман (Boltzmann) Людвиг Австрийский физик, один из основоположников статистической физики и физической кинетики
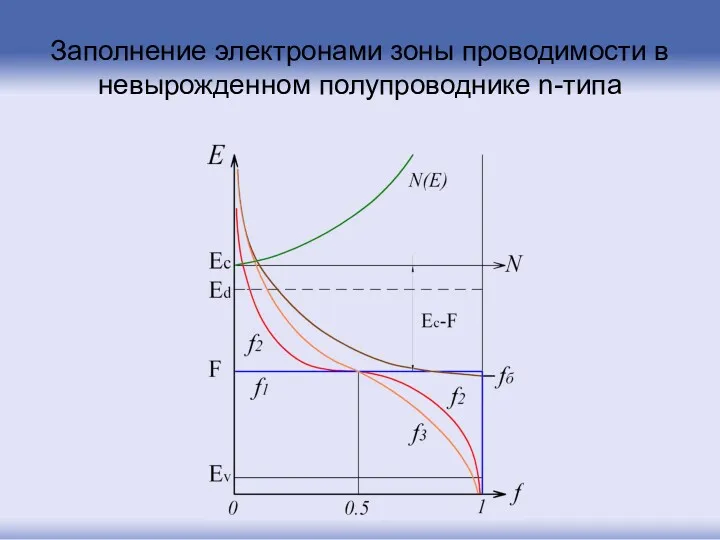
- 117. Заполнение электронами зоны проводимости в невырожденном полупроводнике n-типа
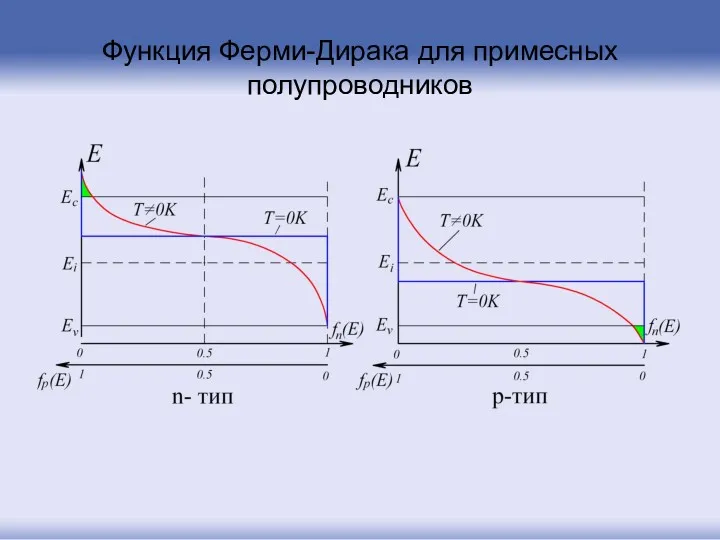
- 118. Функция Ферми-Дирака для примесных полупроводников
- 119. Для невырожденного полупроводника E-F»kT, »1,
- 120. Тогда можно применить статистику Максвелла-Больцмана: Здесь Nс – эффективная плотность состояний в зоне проводимости или плотность
- 121. Заполнение электронами и дырками зон невырожденного полупроводника В частности, для кремния
- 122. Функция распределения Ферми-Дирака для дырок: Функция распределения Максвелла-Больцмана для дырок:
- 123. Для расчета общего количества свободных дырок выполним интегрирование по валентной зоне: Эффективная плотность состояний для валентной
- 124. Эффективная плотность состояний
- 125. Уравнение электронейтральности Для собственного полупроводника: Если в полупроводнике присутствуют как донорная, так и акцепторная примесь
- 126. Расчет положения уровня Ферми для собственного полупроводника
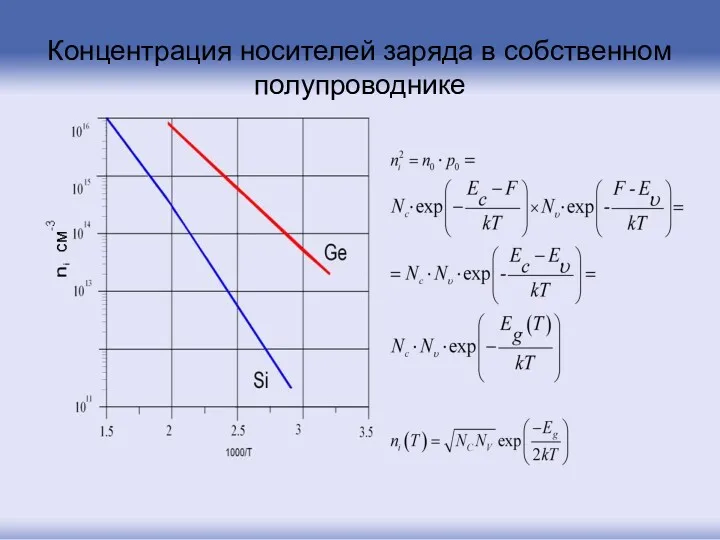
- 127. Концентрация носителей заряда в собственном полупроводнике
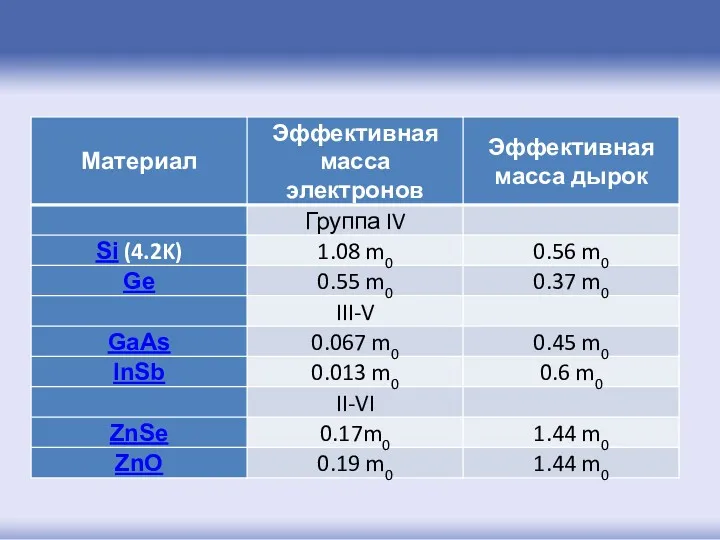
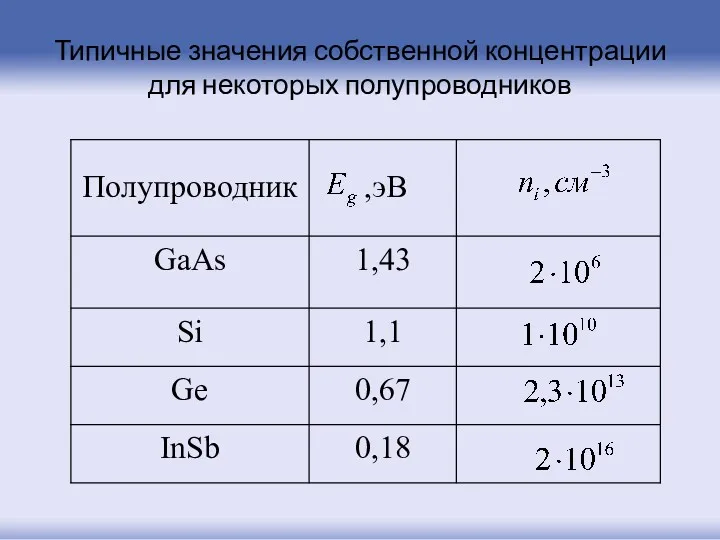
- 128. Типичные значения собственной концентрации для некоторых полупроводников
- 130. Скачать презентацию




















































































 Экологическое образование в процессе обучения физике
Экологическое образование в процессе обучения физике Электрическое поле. Напряженность электрического поля. Принцип суперпозиции полей
Электрическое поле. Напряженность электрического поля. Принцип суперпозиции полей Динамика твердого тела. Лекция 5: Плоское движение твердого тела
Динамика твердого тела. Лекция 5: Плоское движение твердого тела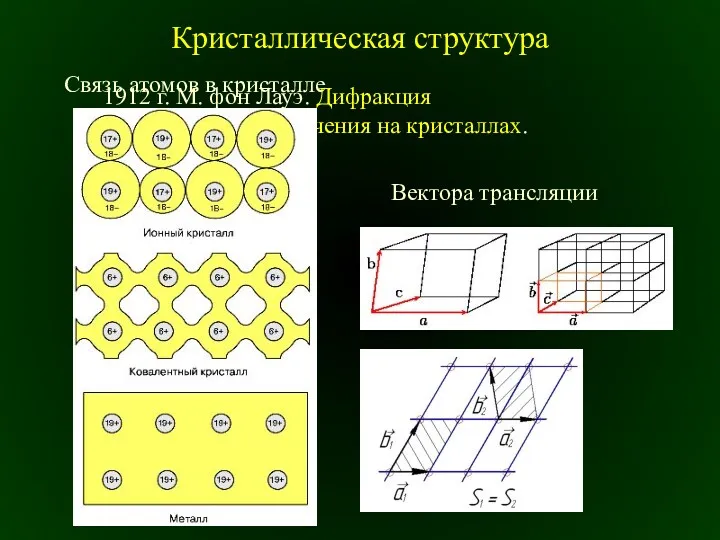 Кристаллическая структура
Кристаллическая структура Фізика в житті сучасної людини
Фізика в житті сучасної людини Mass spectrometry
Mass spectrometry Урок- игра по теме Масса вещества.Плотность
Урок- игра по теме Масса вещества.Плотность Сила упругости 7 класс, презентация
Сила упругости 7 класс, презентация Физико–химические свойства нефти, нефтепродуктов. Качество нефти и нефтепродуктов. Методы их анализа
Физико–химические свойства нефти, нефтепродуктов. Качество нефти и нефтепродуктов. Методы их анализа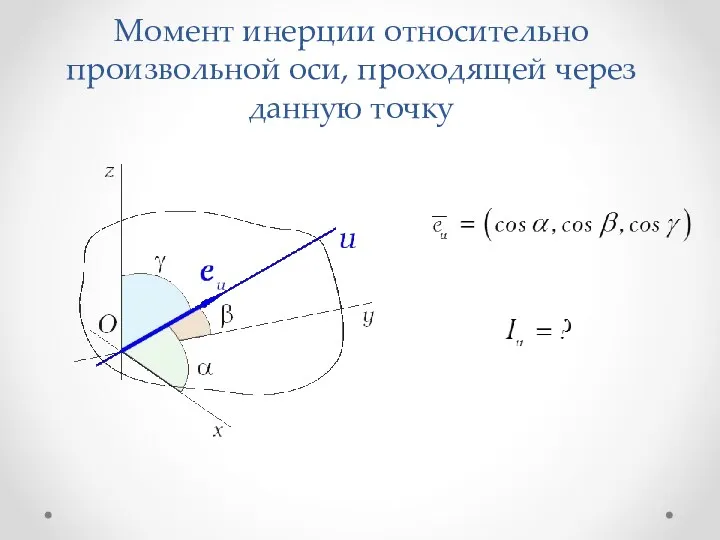 Момент инерции относительно произвольной оси, проходящей через данную точку. (Лекция 5)
Момент инерции относительно произвольной оси, проходящей через данную точку. (Лекция 5) Репортаж с фестиваля наук. Экспериментальная площадка Метеорологическая лаборатория
Репортаж с фестиваля наук. Экспериментальная площадка Метеорологическая лаборатория Формирование исследовательских умений школьников
Формирование исследовательских умений школьников Реактивное движение
Реактивное движение Излучение и спектры
Излучение и спектры Energy and power, solar astronomy. (Lecture 4)
Energy and power, solar astronomy. (Lecture 4) Физика в белом халате
Физика в белом халате Механическое движение
Механическое движение Unusual modes pf transport
Unusual modes pf transport Структура пограничного слоя при продольном обтекании сотовой поверхности
Структура пограничного слоя при продольном обтекании сотовой поверхности Металлический водород
Металлический водород Основные узлы станка
Основные узлы станка Закон радиоактивного распада
Закон радиоактивного распада Озоновый слой атмосферы. Ультрафиолетовое излучение
Озоновый слой атмосферы. Ультрафиолетовое излучение Механическое оборудование и система вентиляции
Механическое оборудование и система вентиляции Спектры и спектральные аппараты. Виды спектров. Спектральный анализ
Спектры и спектральные аппараты. Виды спектров. Спектральный анализ Радиолокация
Радиолокация Паровая машина Ползунова
Паровая машина Ползунова Скорость света
Скорость света