Содержание
- 2. Свободные колебания реальных систем всегда затухают. Затухание обусловлено в основном трением (механические системы) и сопротивлением (
- 3. Уравнения затухающих колебаний Получим дифференциальное уравнение свободных затухающих колебаний на примере реального пружинного маятника, совершающего колебания
- 4. Это уравнение и есть дифференциальное уравнение свободных затухающих колебаний пружинного маятника. Его принято записывать в следующем,
- 5. Рассмотрим свободные затухающие электрические колебания в цепи. R C L Рис. 2 В отличие от ранее
- 6. С точки зрения математики уравнения (2) и (4) одинаковые. Их можно записать в виде: где в
- 7. Из теории дифференциальных уравнений известно, что данное уравнение представляет собой однородное дифференциальное уравнение второго порядка с
- 8. СЛУЧАЙ 2. В этом случае корни уравнения являются Комплексно сопряженными величинами Где Поэтому решение диф. уравнения
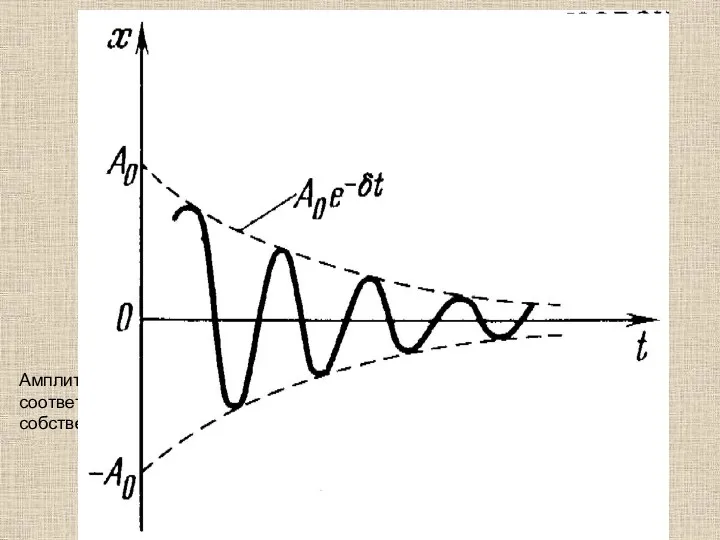
- 9. Амплитуда убывает во времени тем быстрее, чем больше величины b и R в соответствующих системах. Частота
- 10. Амплитуда убывает во времени тем быстрее, чем больше величины b и R в соответствующих системах. Частота
- 11. Это время в физике носит название время релаксации Коэффициент затухания обратен промежутку времени, в течение которого
- 12. Если затухание слабое, тогда Т ≈Т0 Добротности Q любой колебательной системы, способной совершать свободные колебания, может
- 14. Скачать презентацию




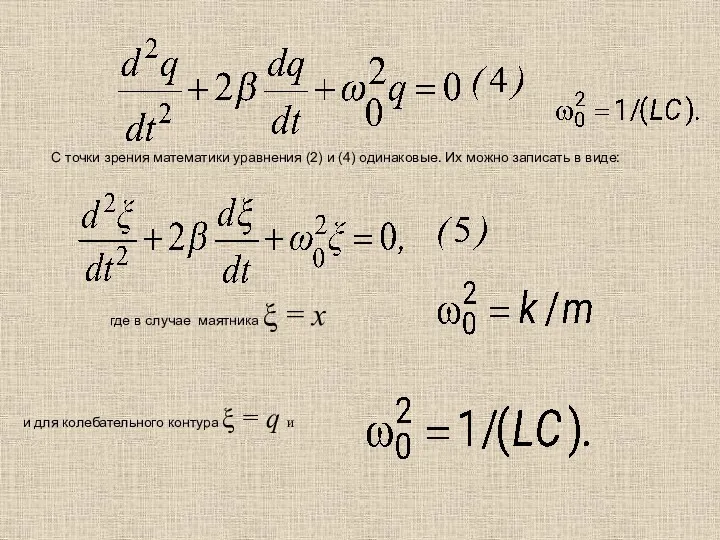





 Закат как физическое явление
Закат как физическое явление Экспериментальные методы исследования частиц
Экспериментальные методы исследования частиц Техническое обслуживание и ремонт автотранспорта МДК 01.01 Устройство автомобилей
Техническое обслуживание и ремонт автотранспорта МДК 01.01 Устройство автомобилей Постоянные магниты (8 класс)
Постоянные магниты (8 класс) Устройство механической коробки передач
Устройство механической коробки передач Формирование ключевых компетенций при решении творческих задач на уроках физики
Формирование ключевых компетенций при решении творческих задач на уроках физики Электростатическое поле в вакууме
Электростатическое поле в вакууме Электричество и его использование
Электричество и его использование Введение в тепловое моделирование
Введение в тепловое моделирование Растяжение и сжатие
Растяжение и сжатие презентация Проще простого тепловые явления или Физика за чашкой чая
презентация Проще простого тепловые явления или Физика за чашкой чая презентация Интеграция как один из способов повышения качества обучения на уроках физики
презентация Интеграция как один из способов повышения качества обучения на уроках физики Явление электромагнитной индукции
Явление электромагнитной индукции открытый урок тепловые машины
открытый урок тепловые машины Основные законы электротехники
Основные законы электротехники Гравітаційне поле. Сила тяжіння. Перша космічна швидкість. Урок 21. Фізика. 10 клас
Гравітаційне поле. Сила тяжіння. Перша космічна швидкість. Урок 21. Фізика. 10 клас Атом ядросының модельдерінің түрлерІ
Атом ядросының модельдерінің түрлерІ Попов Александр Степанович
Попов Александр Степанович Терминалы
Терминалы Архимедова сила. Архимед (287-212 до н.э.)
Архимедова сила. Архимед (287-212 до н.э.) Молекулярная физика. Лекция 9
Молекулярная физика. Лекция 9 Анализ, диагностика, техническое обслуживание и ремонт комплексной системы управления двигателем (КСАУ-Д) Lada Priora
Анализ, диагностика, техническое обслуживание и ремонт комплексной системы управления двигателем (КСАУ-Д) Lada Priora презентация решение задач по теме Простые механизмы
презентация решение задач по теме Простые механизмы Ознакомление с автомобилем 580 и его системами
Ознакомление с автомобилем 580 и его системами Колесные пары тепловозов
Колесные пары тепловозов What’s the Connection? Forces and Motion
What’s the Connection? Forces and Motion Introduction to Quantum Mechanic
Introduction to Quantum Mechanic Electromagnetic Waves Scale. Uses of Electromagnetic Waves
Electromagnetic Waves Scale. Uses of Electromagnetic Waves