Содержание
- 2. Уравнение Лагранжа Основная задача динамики в обобщенных координатах Случай потенциальных сил Рекомендации к решению задач Задача
- 3. УРАВНЕНИЕ ЛАГРАНЖА II- РОДА Уравнения Лагранжа второго рода Цель: Получить систему Д.У. для определения законов движения
- 4. УРАВНЕНИЕ ЛАГРАНЖА II- РОДА независимы, каждый из коэффициентов при равен нулю (1) Выразим Сила инерции любой
- 5. УРАВНЕНИЕ ЛАГРАНЖА II- РОДА Тогда (2а) с учетом (4) запишется в виде Дифференцируем (3) по (4)
- 6. УРАВНЕНИЕ ЛАГРАНЖА II- РОДА Таким образом, Мы получили уравнения Лагранжа второго рода
- 7. УРАВНЕНИЕ ЛАГРАНЖА II- РОДА Основная задача динамики в обобщенных координатах состоит в том, чтобы, зная обобщенные
- 8. УРАВНЕНИЕ ЛАГРАНЖА II- РОДА 1. Решить основную (обратную) задачи динамики в обобщенных координатах – по известным
- 9. РЕКОМЕНДАЦИИ К РЕШЕНИЮ Л- II Рекомендации к решению 1. Выбрать механическую систему и проверить связи на
- 10. РЕКОМЕНДАЦИИ К РЕШЕНИЮ Л- II Рекомендации к решению Л-II 4. Получить зависимость кинетической энергии в виде
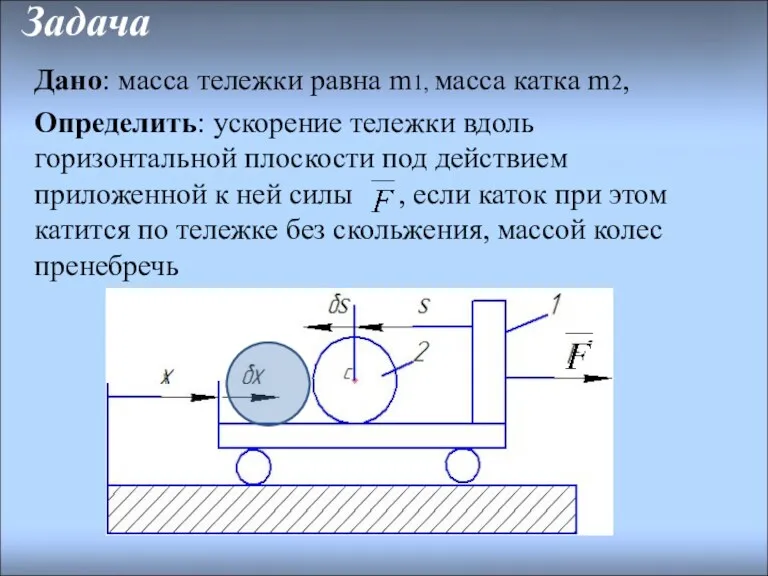
- 11. Задача Дано: масса тележки равна m1, масса катка m2, Определить: ускорение тележки вдоль горизонтальной плоскости под
- 12. Решение Система имеет две степени свободы . В качестве обобщенных координат выберем координату x тележки и
- 13. -Для сплошного цилиндра а при качении без скольжения где -относительная скорость центра С по отношению к
- 14. 3. Дадим системе возможное перемещение, при котором координата х получает приращение δx>0 . На этом перемещении
- 15. 5. Допустим, что трения катка о тележку нет. Тогда он по тележке будет скользить, двигаясь поступательно,
- 16. Заключение ЗАКЛЮЧЕНИЕ 1. В обобщенных координатах принцип Даламбера-Лагранжа принимает вид уравнений Лагранжа второго рода 2. Уравнения
- 18. Скачать презентацию














 Корпусные детали, смазочные и уплотняющие устройства
Корпусные детали, смазочные и уплотняющие устройства Тепловое излучение и его характеристики
Тепловое излучение и его характеристики Електротехніка (Лекція 6. Частина 2)
Електротехніка (Лекція 6. Частина 2) Строение атома
Строение атома Урок Атмосфера и атмосферное давление
Урок Атмосфера и атмосферное давление Физический диктант
Физический диктант Строение атома
Строение атома Физико-технические основы электроэнергетики. Лекция 10
Физико-технические основы электроэнергетики. Лекция 10 Игра Кто хочет стать миллионером? по физике
Игра Кто хочет стать миллионером? по физике Конструкция автомобиля. Коробка передач. Назначение и типы. Общее устройство и принцип работы
Конструкция автомобиля. Коробка передач. Назначение и типы. Общее устройство и принцип работы Метод неразрушающего определения теплопроводности защитного покрытия из ПВХ на стальном изделии
Метод неразрушающего определения теплопроводности защитного покрытия из ПВХ на стальном изделии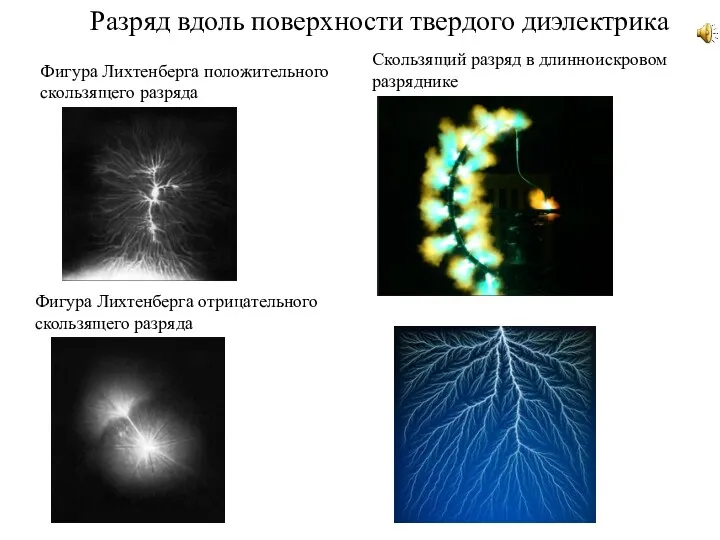 Разряд вдоль поверхности твердого диэлектрика. (Лекция 4)
Разряд вдоль поверхности твердого диэлектрика. (Лекция 4) Раздел 1. Акустические преобразователи. Классификация
Раздел 1. Акустические преобразователи. Классификация Элементарные частицы
Элементарные частицы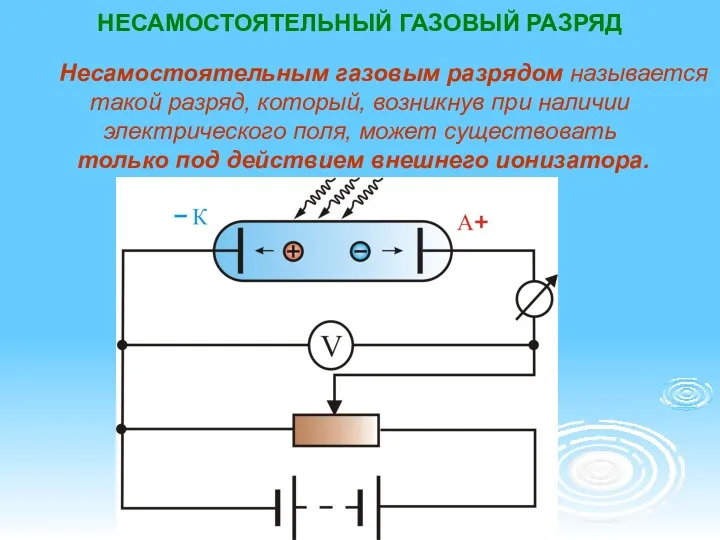 Ток в газах
Ток в газах урок-беседа с элементами поиска по теме Исследование изотермического процесса в 10 классе
урок-беседа с элементами поиска по теме Исследование изотермического процесса в 10 классе Электромагнитные волны
Электромагнитные волны Измерение рычажно-механическими приборами
Измерение рычажно-механическими приборами Рівняння стану ідеального газу. Ізопроцеси
Рівняння стану ідеального газу. Ізопроцеси радиоактивность
радиоактивность Выступление на заседании МО учителей естественно-математического цикла Формирование УУД учащихся 7 класса на уроках физики
Выступление на заседании МО учителей естественно-математического цикла Формирование УУД учащихся 7 класса на уроках физики Mercedes ML 2000-2005
Mercedes ML 2000-2005 Припои и флюсы
Припои и флюсы Самоанализ учителя физики
Самоанализ учителя физики Примеси и примесные состояния в полупроводниках
Примеси и примесные состояния в полупроводниках Электрические явления.
Электрические явления. Нанокомпозиты
Нанокомпозиты Механическая работа, мощность. 7 класс
Механическая работа, мощность. 7 класс