Содержание
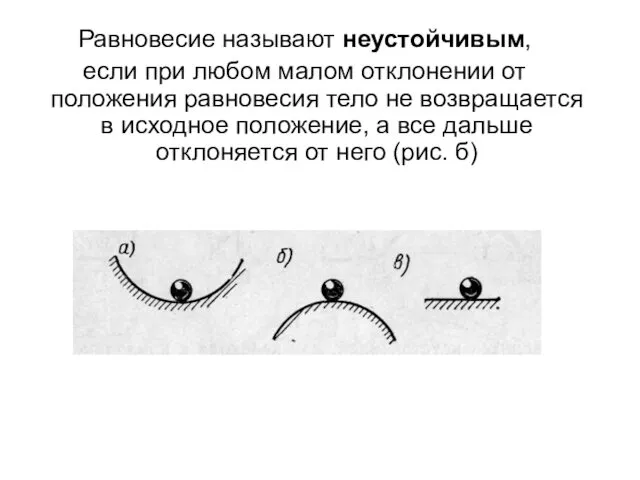
- 2. Равновесие называют неустойчивым, если при любом малом отклонении от положения равновесия тело не возвращается в исходное
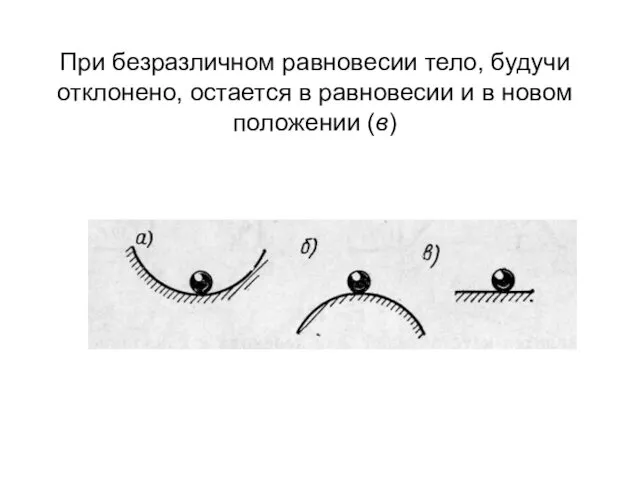
- 3. При безразличном равновесии тело, будучи отклонено, остается в равновесии и в новом положении (в)
- 4. Для задач механики абсолютно твердого тела характерно, что вид равновесия не зависит от значений действующих на
- 5. Рассмотрим сравнительно длинный и тонкий прямолинейный стержень, нагруженный центрально приложенной сжимающей силой. Если приложить к стержню
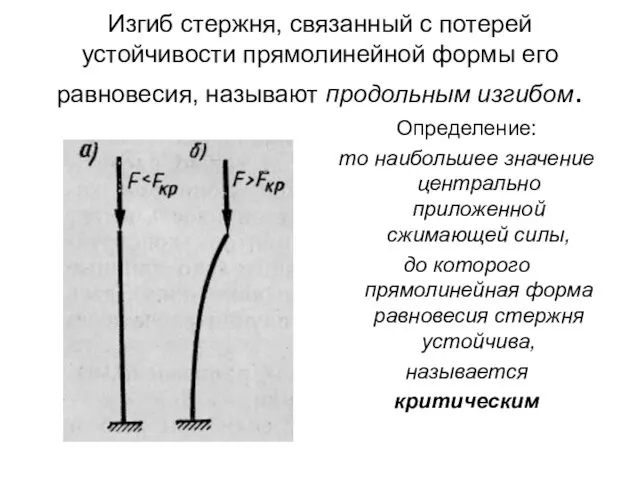
- 6. Изгиб стержня, связанный с потерей устойчивости прямолинейной формы его равновесия, называют продольным изгибом. Определение: то наибольшее
- 7. Если при силе, незначительно большей критической, стержень не разрушается в буквальном смысле слова, то конструкция все
- 8. Расчет на устойчивость должен обеспечить работу элемента конструкции при первоначальной форме его упругого равновесия, т.е. при
- 9. Условие устойчивости прямолинейной формы равновесия стержня может быть представлено так: где - допускаемое значение силы, сжимающей
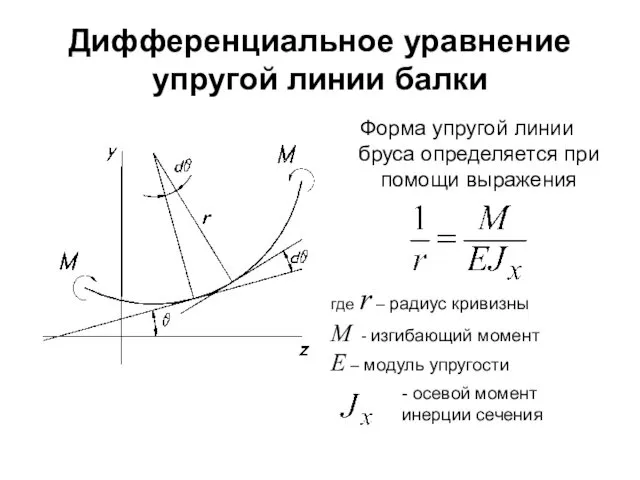
- 10. Дифференциальное уравнение упругой линии балки Форма упругой линии бруса определяется при помощи выражения где r –
- 11. Учитывая, что получаем дифференциальные уравнение упругой линии
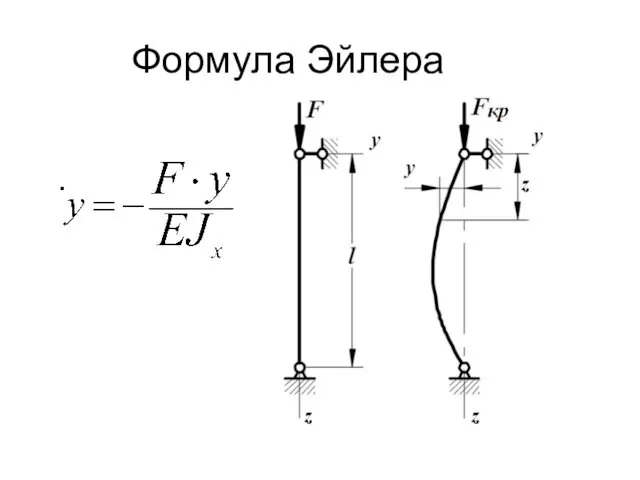
- 12. Формула Эйлера Рассмотрим вопрос о критической силе сжатого стержня, оба конца которого закреплены шарнирно. Пусть стержень
- 13. Формула Эйлера
- 14. В результате решения этого дифференциального уравнения и использования граничных условий, определяемых способами закрепления концов стержня, получается
- 15. Значения А к В определяются из граничных условий. При z=0; y=0. Тогда при z = l;
- 16. или Пример шарнирного закрепления обоих концов стержня, когда его изогнутая ось при потере устойчивости представляет собой
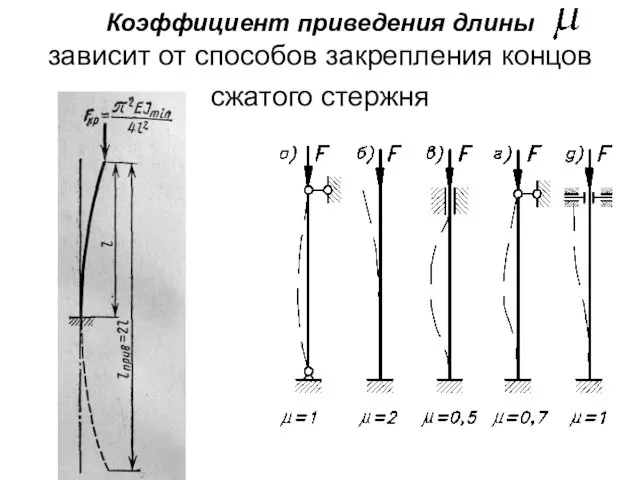
- 17. Коэффициент приведения длины зависит от способов закрепления концов сжатого стержня
- 18. Приведенную длину стержня удобно выразить через фактическую длину и некоторый коэффициент μ, зависящий от способов закрепления
- 19. Критическое напряжение. Пределы применимости формулы Эйлера. Нормальное напряжение в поперечном сечении сжатого стержня, соответствующее критическому значению
- 20. Геометрическую характеристику сечения называют радиусом инерции сечения относительно данной оси Таким образом, или
- 21. Отношение приведенной длины стержня к минимальному радиусу инерции его поперечного сечения называют гибкостью стержня (или стойки).
- 22. Используя понятие гибкости λ стержня, получаем следующую окончательную формулу для критического напряжения: При выводе формулы Эйлера
- 23. или отсюда Величину, стоящую в правой части этого неравенства, обозначим и назовем предельной гибкостью (иногда говорят
- 24. В отличие от гибкости стержня, представляющей собой его геометрическую характеристику, предельная гибкость зависит только от физико-механических
- 25. В качестве примера вычислим значение для углеродистой стали 45, имеющей модуль продольной упругости и предел пропорциональности
- 26. В случае неприменимости формулы Эйлера критические напряжения определяются по эмпирическим формулам, составленным Ф.С.Ясинским на основе опытов,
- 27. В зависимости от гибкости сжатые стержни условно делят на три категории: 1. Стержни большой гибкости для
- 28. 2. Стержни средней гибкости рассчитываемые на устойчивость по эмпирической формуле Ф.С.Ясинского.
- 29. 3. Стержни малой гибкости рассчитываемые не на устойчивость, а на прочность Для них критическое напряжение считается
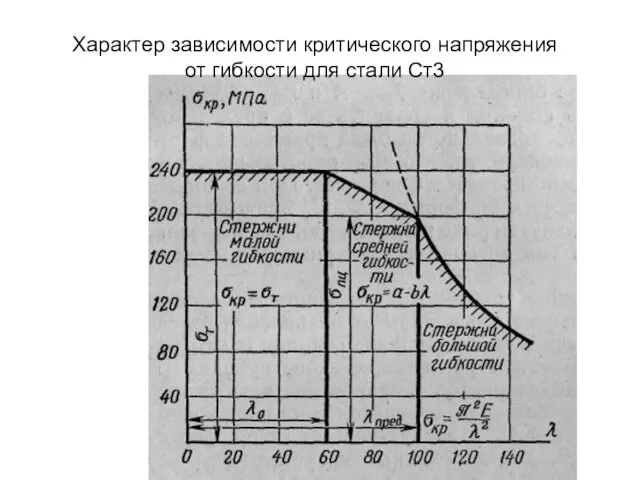
- 30. Характер зависимости критического напряжения от гибкости для стали Ст3
- 31. Ясинский Феликс Станиславович 1856 - 1899 Окончил Петербургский институт инженеров путей сообщения. В 1890 г. был
- 32. Расчет сжатых стержней на устойчивость по коэффициентам продольного изгиба Расчет сжатых стержней на устойчивость можно по
- 33. где допускаемое напряжение при расчете на устойчивость. Обычно выражают через основное допускаемое напряжение на сжатие для
- 34. Связь между коэффициентом φ, критическим напряжением , предельным напряжением и коэффициентами запаса прочности [n] и устойчивости
- 35. Значение коэффициента φ зависит от материала стержня и от его гибкости. Для строительных конструкций значения этих
- 36. Этот метод расчета универсален в том смысле, что он не связан с пределами применимости формулы Эйлера
- 37. Расчет сжатого стержня по коэффициенту продольного изгиба φ внешне совершенно подобен расчету на простое сжатие, но
- 39. Скачать презентацию





























 Химия функциональных материалов. Диэлектрические материалы
Химия функциональных материалов. Диэлектрические материалы Обобщающий урок-викторина по физике в 7 классе по теме Взаимодействие тел
Обобщающий урок-викторина по физике в 7 классе по теме Взаимодействие тел Необслуживаемые автомобильные аккумуляторы
Необслуживаемые автомобильные аккумуляторы Закон всемирного тяготения. Сила тяжести. Вес
Закон всемирного тяготения. Сила тяжести. Вес Электромагниттік сәуле шығару
Электромагниттік сәуле шығару Электрическое сопротивление
Электрическое сопротивление Метрология, стандартизация и сертификация. Взаимозаменяемость
Метрология, стандартизация и сертификация. Взаимозаменяемость ЕГЭ по физике
ЕГЭ по физике Ядерный реактор
Ядерный реактор Электростатическое поле в диэлектриках. (Лекция 4)
Электростатическое поле в диэлектриках. (Лекция 4) Презентация к уроку Электромагнитные волны в 11 классе
Презентация к уроку Электромагнитные волны в 11 классе Радиоактивность. Урок физики 11 класс
Радиоактивность. Урок физики 11 класс Магнітні властивості речовини
Магнітні властивості речовини ”Равноускоренное движение”
”Равноускоренное движение” Напряженность электрического поля. Принцип суперпозиции полей
Напряженность электрического поля. Принцип суперпозиции полей Расчет на прочность. (Лекция 6)
Расчет на прочность. (Лекция 6) Термодинамические процессы
Термодинамические процессы Работа Электрического тока
Работа Электрического тока Рулевое управление
Рулевое управление Ремонт автомобилей. Восстановление деталей с применением синтетических материалов. (Тема 3.7)
Ремонт автомобилей. Восстановление деталей с применением синтетических материалов. (Тема 3.7)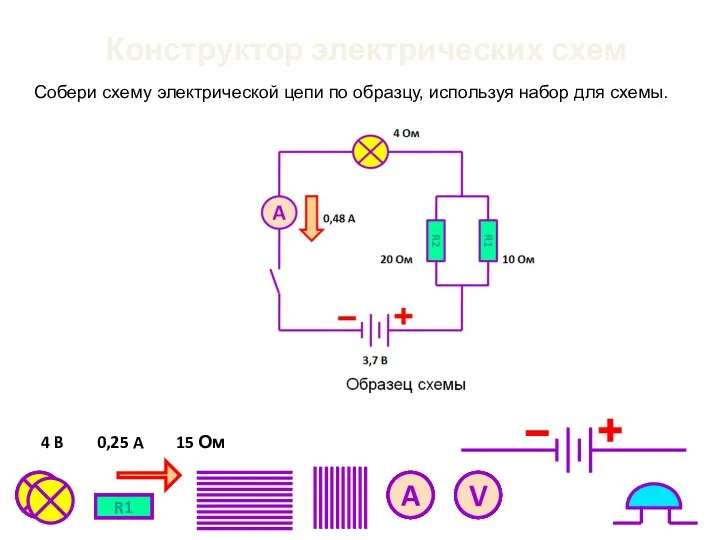 Конструктор электрических схем.
Конструктор электрических схем. Хроматография
Хроматография Поверхностное натяжение жидкости
Поверхностное натяжение жидкости Электрический ток. Сила тока
Электрический ток. Сила тока Технология обработки типовых деталей машин
Технология обработки типовых деталей машин Развитие средств связи
Развитие средств связи Явления в природе. Физические явления
Явления в природе. Физические явления Перемещение при прямолинейном равноускоренном движении
Перемещение при прямолинейном равноускоренном движении