Содержание
- 2. Треугольник Часто знает и дошкольник, Что такое треугольник, А уж вам-то, как не знать… Но совсем
- 3. Определите своё эмоциональное состояние в начале урока. Поставьте галочку в клетку, соответствующую настроению Психологическая разминка
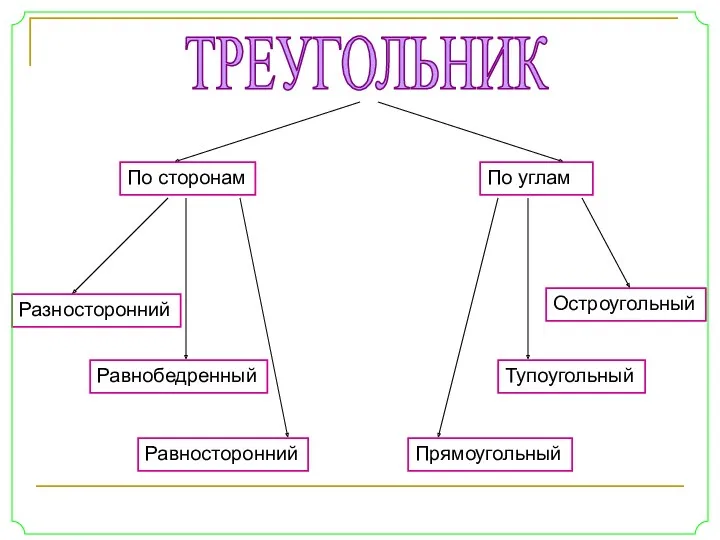
- 4. ТРЕУГОЛЬНИК По сторонам По углам Разносторонний Равнобедренный Равносторонний Остроугольный Тупоугольный Прямоугольный
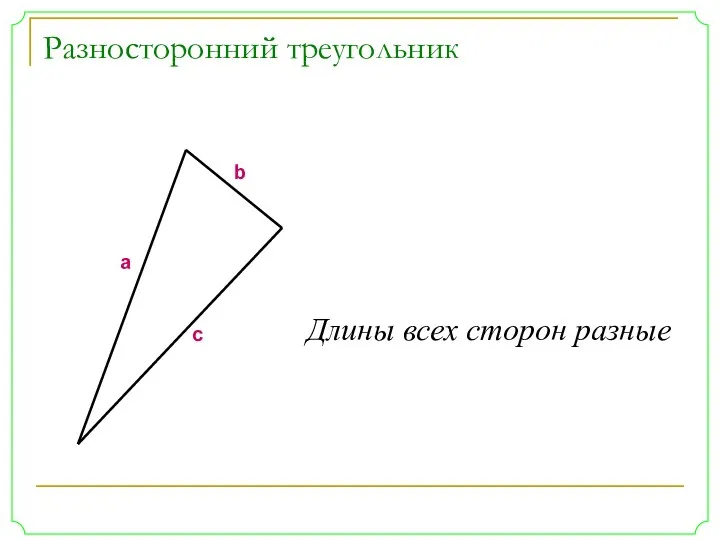
- 5. Разносторонний треугольник a b c Длины всех сторон разные
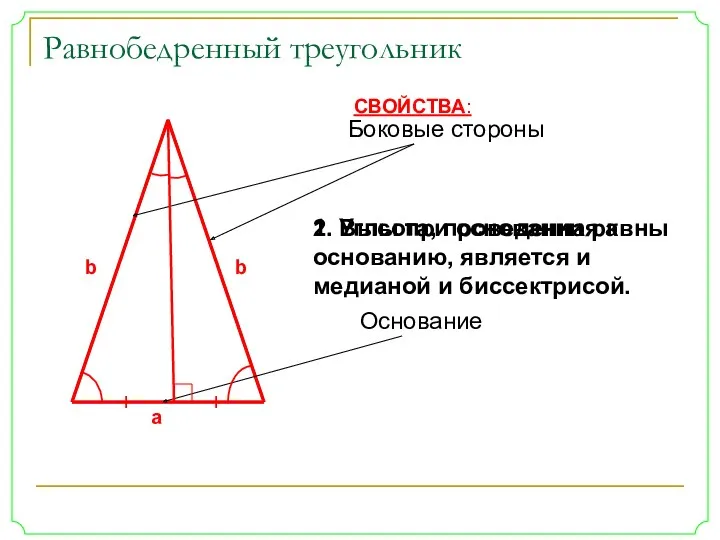
- 6. Равнобедренный треугольник b b Боковые стороны а Основание СВОЙСТВА: 1. Углы при основании равны 2. Высота,
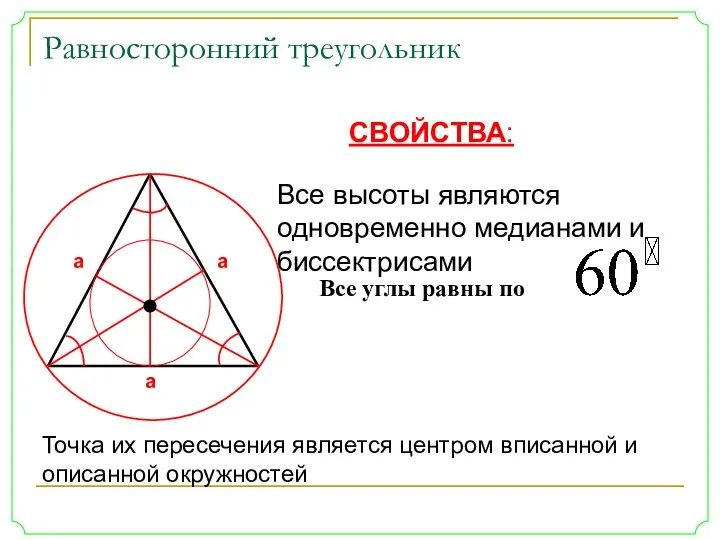
- 7. Равносторонний треугольник а а а СВОЙСТВА: Все углы равны по Все высоты являются одновременно медианами и
- 8. Классификация по углам: остроугольный треугольник, в котором все углы острые; тупоугольный треугольник, в котором один из
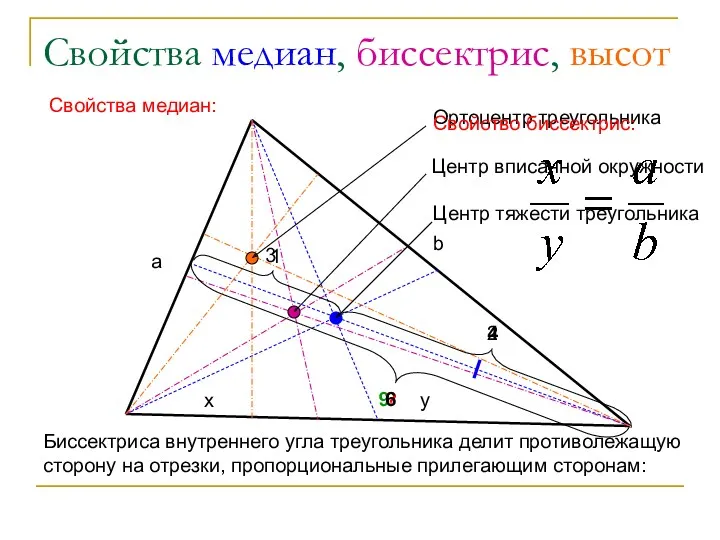
- 9. Свойства медиан, биссектрис, высот 2 1 3 ? 9 4 6 Центр тяжести треугольника Центр вписанной
- 10. «Решение треугольников» Что это значит?
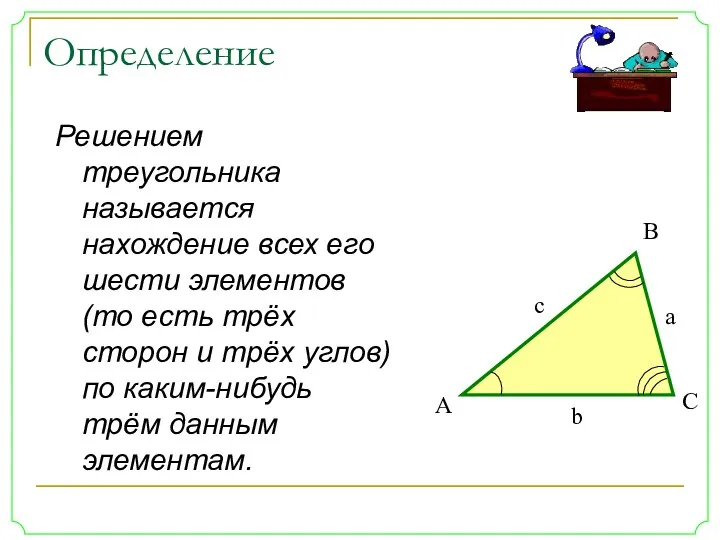
- 11. Определение Решением треугольника называется нахождение всех его шести элементов (то есть трёх сторон и трёх углов)
- 12. Три типа задач на решение треугольника Решение треугольника по двум сторонам и углу между ними; Решение
- 13. Для этого вспомним Решение данных задач основано на использовании теорем синуса и косинуса, теоремы о сумме
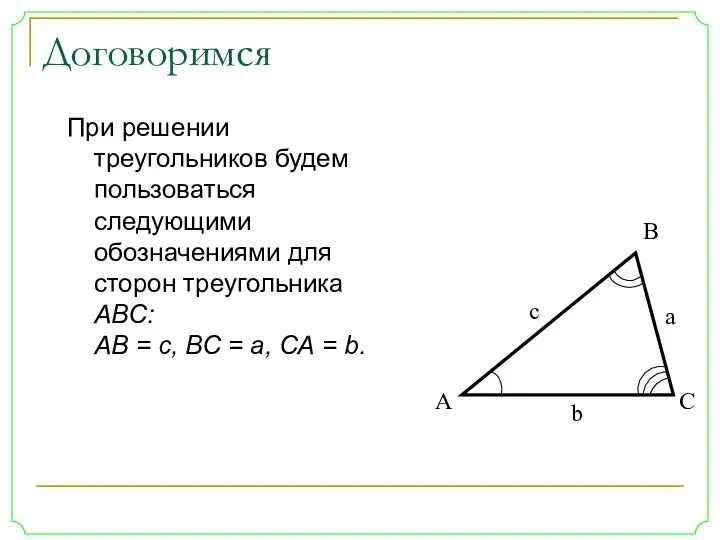
- 14. Договоримся При решении треугольников будем пользоваться следующими обозначениями для сторон треугольника ABC: АВ = с, ВС
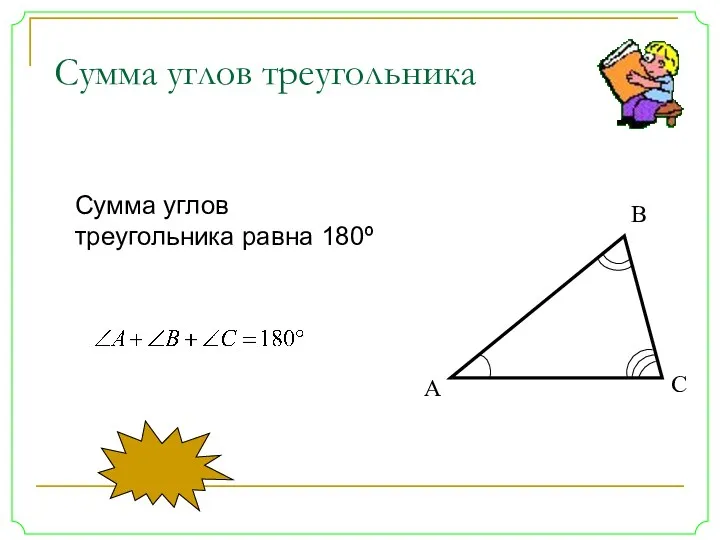
- 15. А В С Сумма углов треугольника Сумма углов треугольника равна 180º
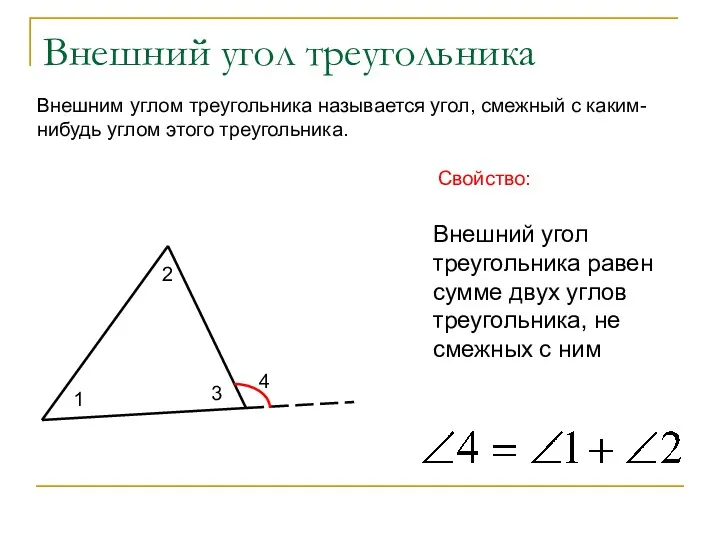
- 16. Внешний угол треугольника Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника. Свойство: Внешний
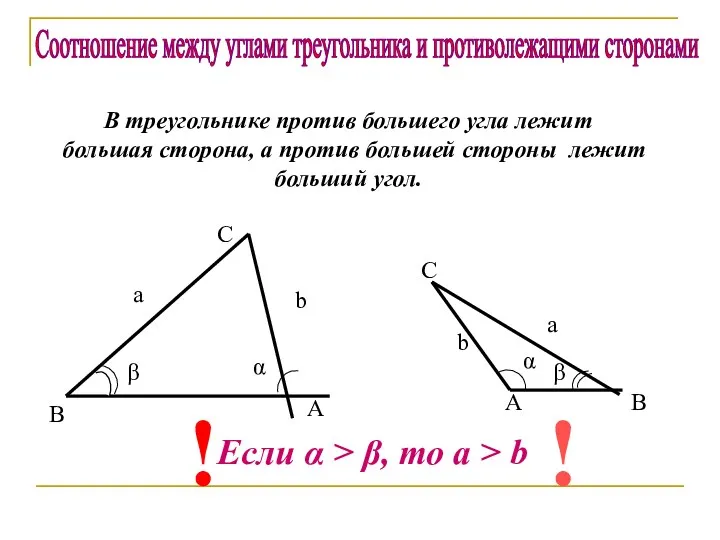
- 17. b ! Соотношение между углами треугольника и противолежащими сторонами В треугольнике против большего угла лежит
- 18. Неравенство треугольника Каждая сторона треугольника меньше суммы двух других сторон. Пусть a, b, c – длины
- 19. В треугольнике против угла в 150º лежит большая сторона. В равностороннем треугольнике внутренние углы равны между
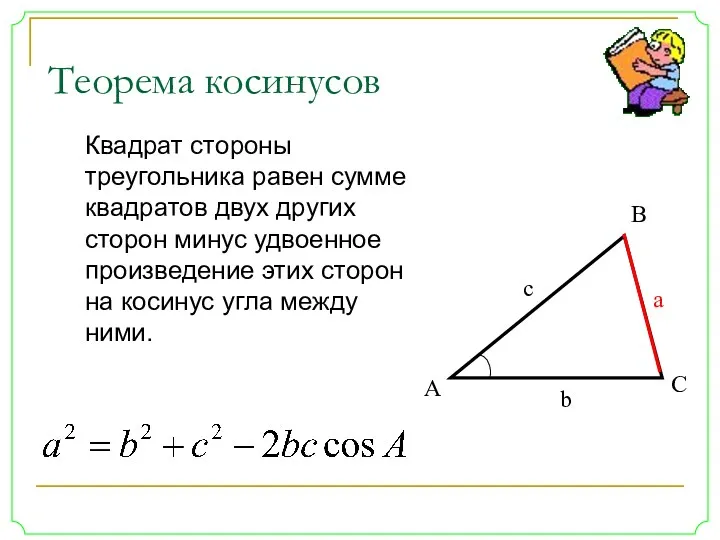
- 20. Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус
- 21. Определение вида треугольника Следовательно, треугольник, у которого a – наибольшая сторона, будет: если cos А ,
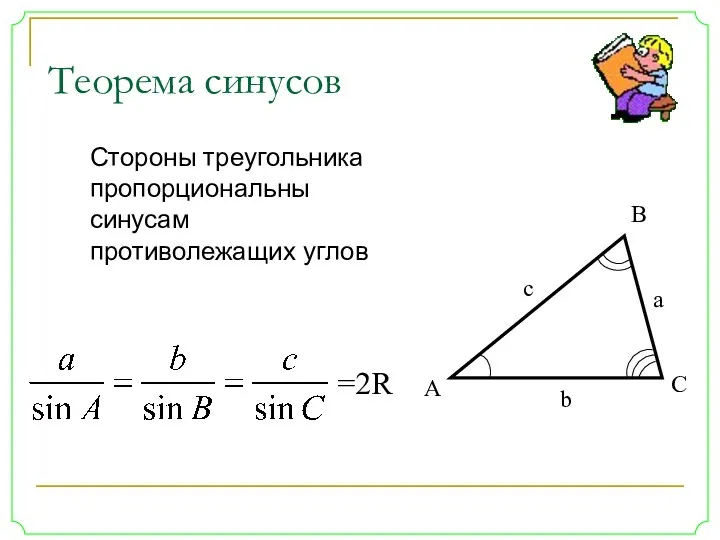
- 22. Стороны треугольника пропорциональны синусам противолежащих углов Теорема синусов =2R
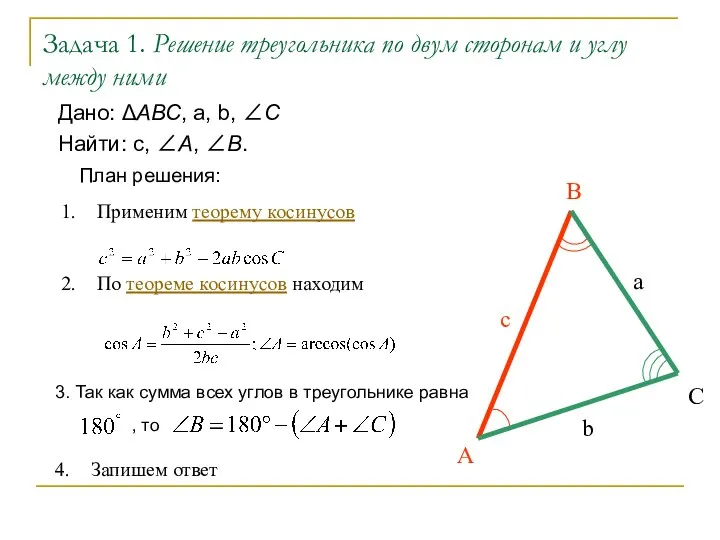
- 23. Задача 1. Решение треугольника по двум сторонам и углу между ними Дано: АВС, а, b, C
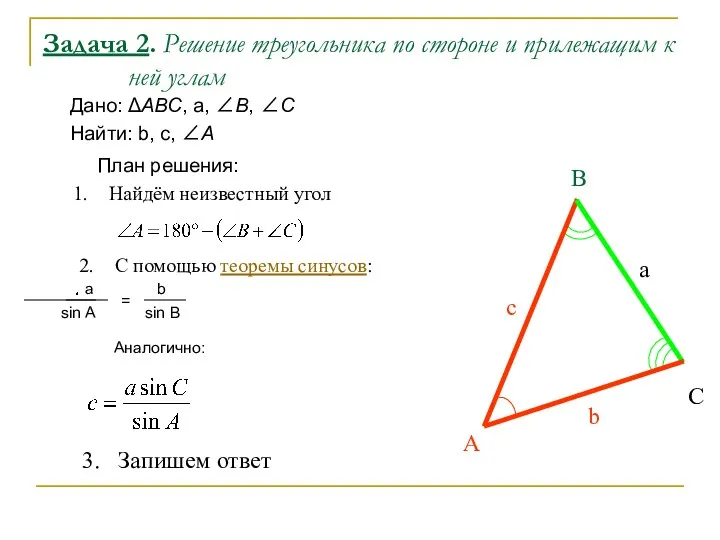
- 24. Задача 2. Решение треугольника по стороне и прилежащим к ней углам Дано: АВС, а, В, С
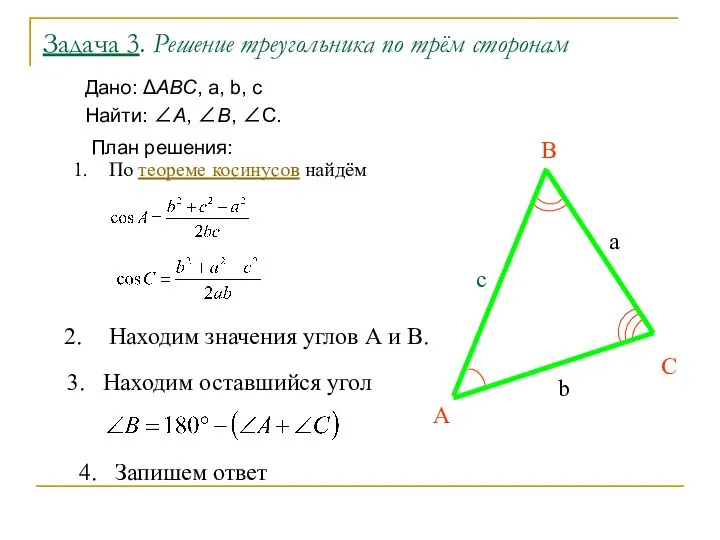
- 25. Задача 3. Решение треугольника по трём сторонам Дано: АВС, a, b, c Найти: А, В, С.
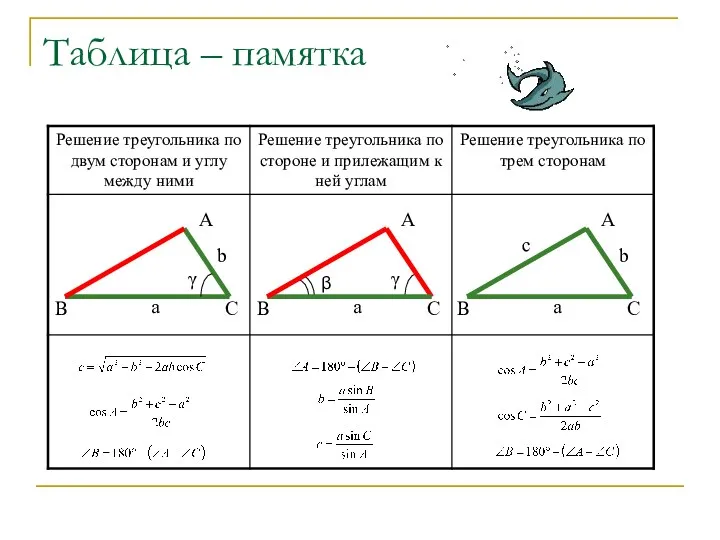
- 26. Таблица – памятка А С a b В А С γ a β В А С
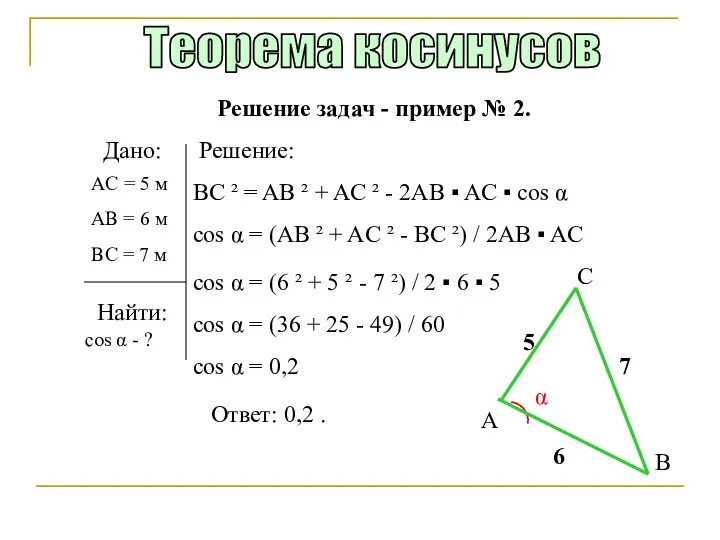
- 27. Задачи для самостоятельного решения АС=5м, АВ=6 м, cos A=0,6. Найти ВС. АС= 5 м, АВ= 6
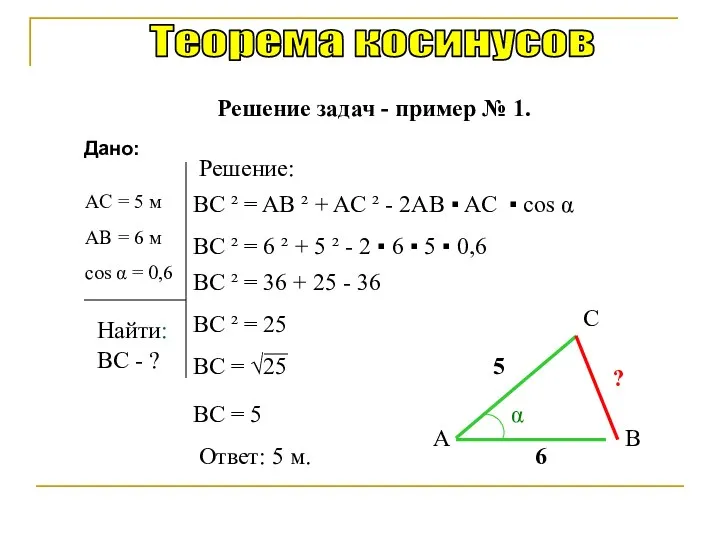
- 28. Теорема косинусов Найти: Решение: AC = 5 м BC - ? A B C BC
- 29. BC ² = AB ² + AC ² - 2AB AC cos Теорема
- 30. Теорема синусов Дано: Найти: Решение: = 45° b - ? A B C a
- 31. Математическая пауза
- 32. ПЛОЩАДЬ ТРЕУГОЛЬНИКА
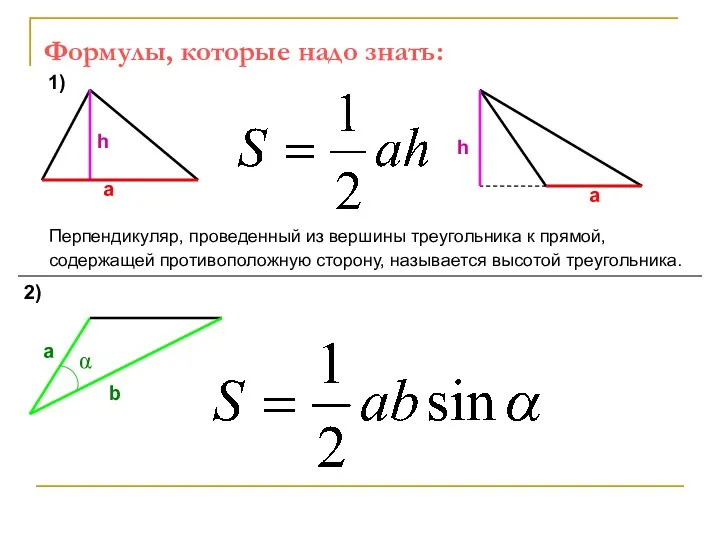
- 33. Формулы, которые надо знать: а h а h Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей
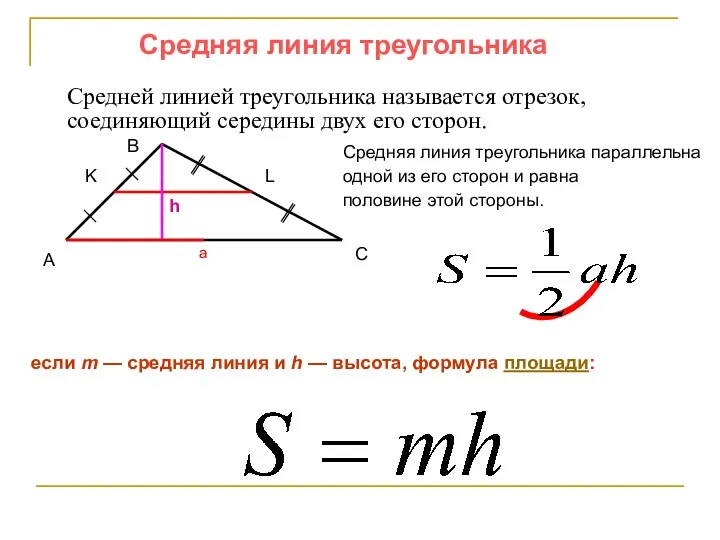
- 34. Средняя линия треугольника Средней линией треугольника называется отрезок, соединяющий середины двух его сторон. А B C
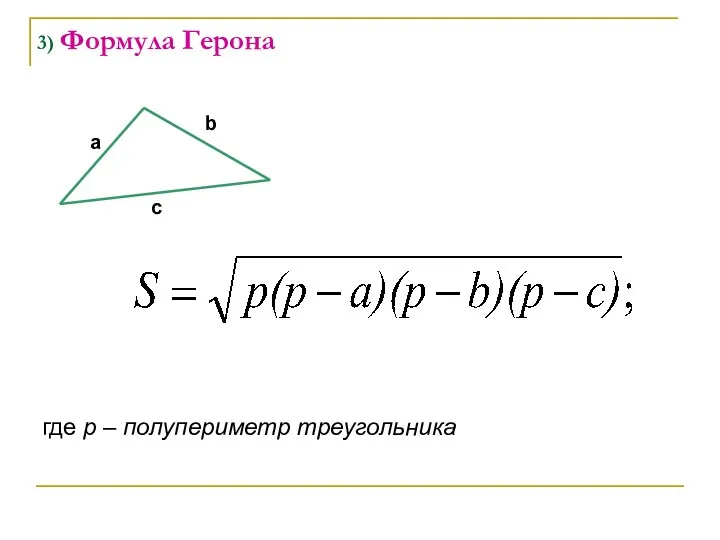
- 35. 3) Формула Герона а b c где p – полупериметр треугольника
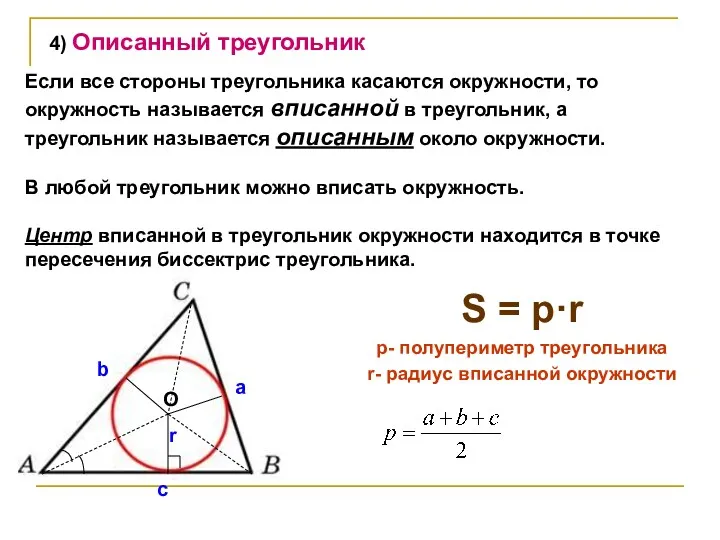
- 36. S = p·r p- полупериметр треугольника r- радиус вписанной окружности a c b r 4) Описанный
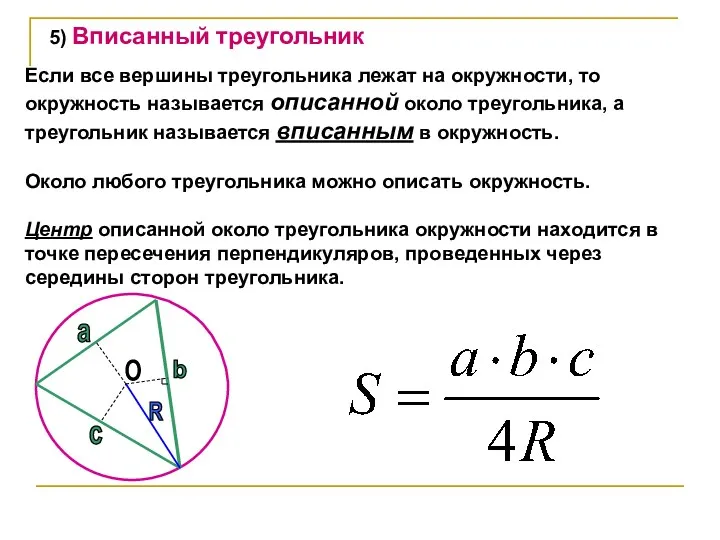
- 37. 5) Вписанный треугольник Если все вершины треугольника лежат на окружности, то окружность называется описанной около треугольника,
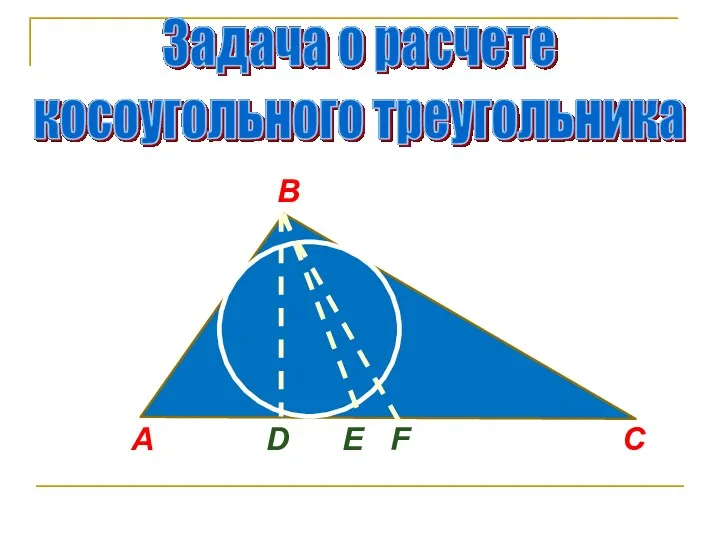
- 38. B A C D Е F
- 39. ЭТАПЫ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ: 1. ЧТЕНИЕ УСЛОВИЯ ЗАДАЧИ. 2. ВЫПОЛНЕНИЕ ЧЕРТЕЖА С БУКВЕННЫМИ ОБОЗНАЧЕНИЯМИ. 3. КРАТКАЯ
- 40. ЭТАПЫ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ: 6. «ДЕТАЛИРОВКА» — ВЫЧЕРЧИВАНИЕ ОТДЕЛЬНЫХ ДЕТАЛЕЙ НА ДОПОЛНИТЕЛЬНЫХ ЧЕРТЕЖАХ. 7. АНАЛИЗ ДАННЫХ
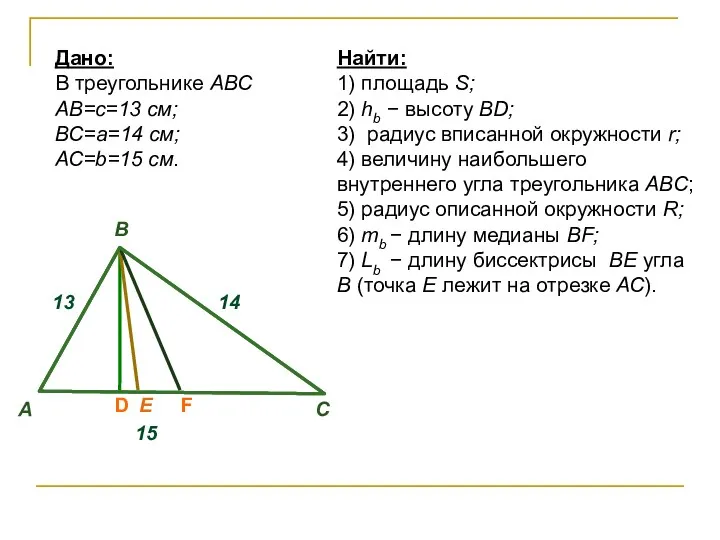
- 41. Найти: 1) площадь S; 2) hb − высоту BD; 3) радиус вписанной окружности r; 4) величину
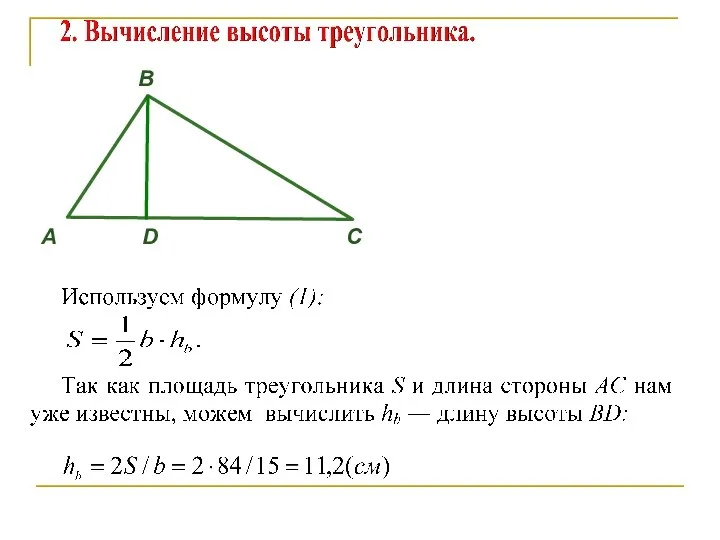
- 44. B А D C
- 45. B А C Отсюда находим
- 46. Из этой теоремы следует, что большим углом в треугольнике АВС является угол В. По формуле (2)
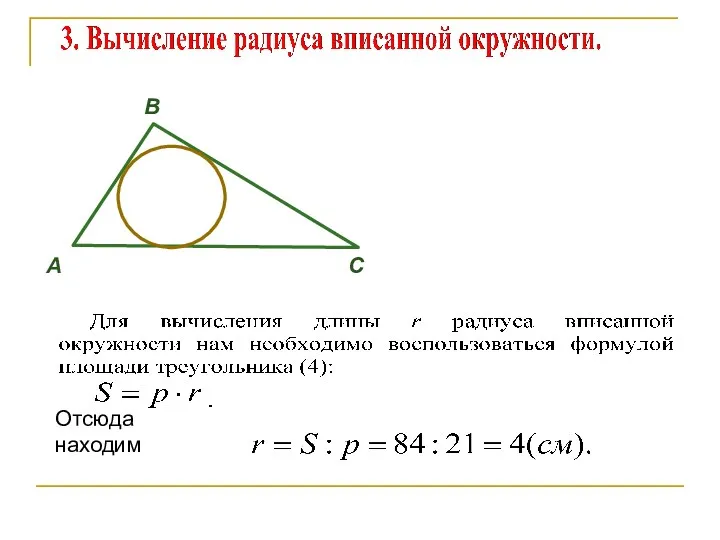
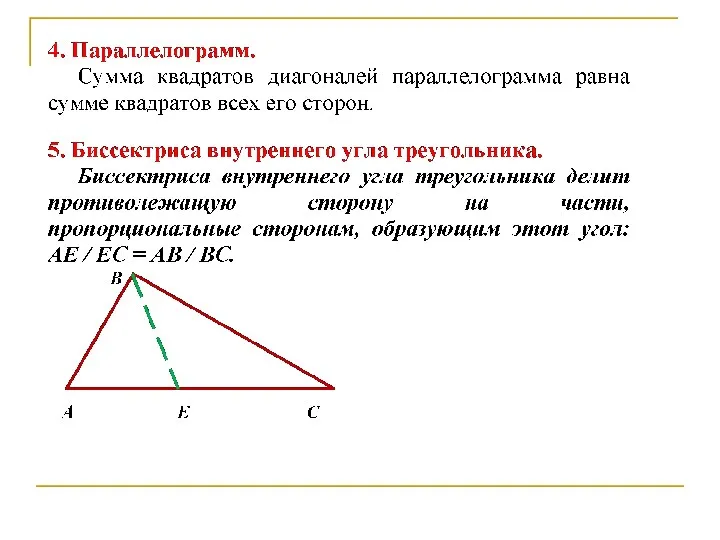
- 47. 5. Вычисление радиуса описанной окружности.
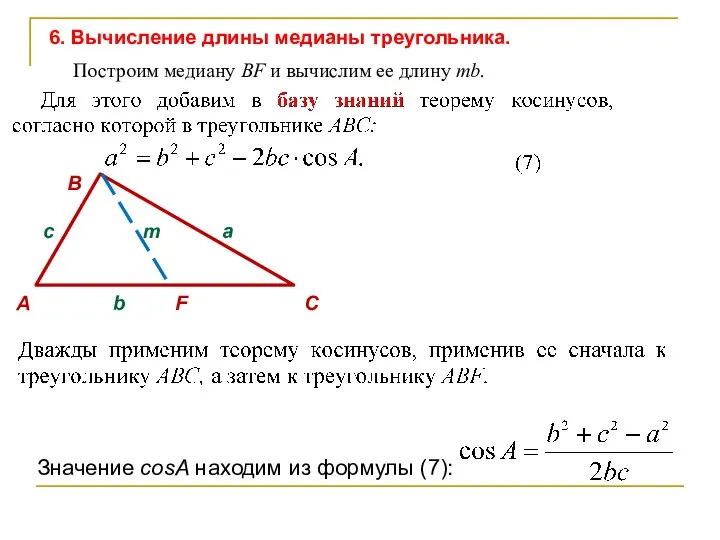
- 48. c m a А b F C B 6. Вычисление длины медианы треугольника. Построим медиану BF
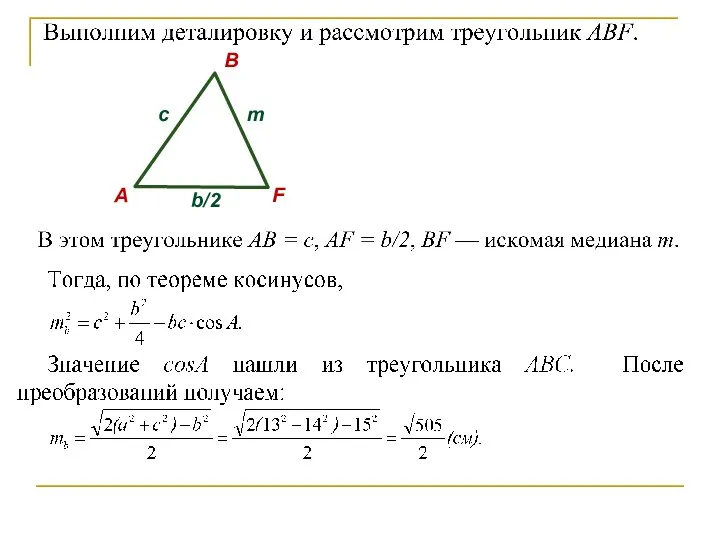
- 49. B А F c m b/2
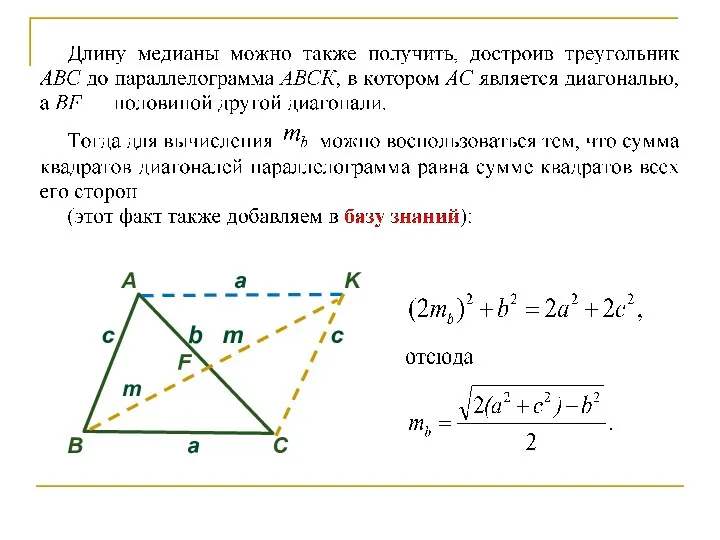
- 50. A a K c b m c F m B a C
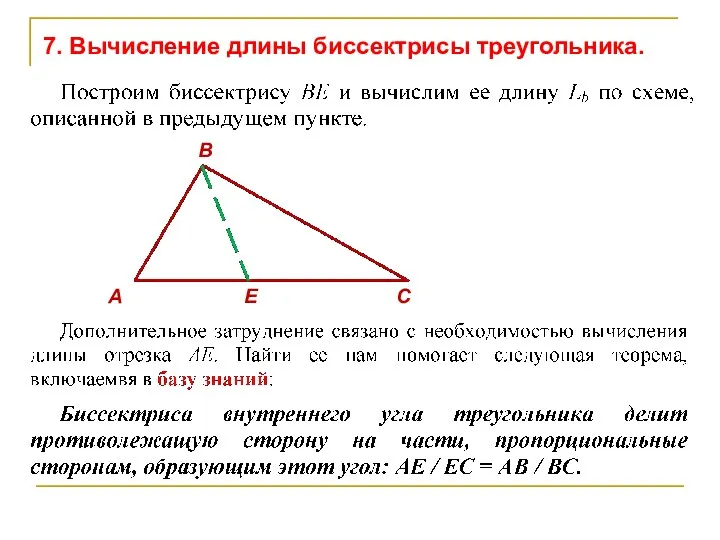
- 51. А E C B 7. Вычисление длины биссектрисы треугольника.
- 52. В c L a А Е С Обозначим AE = x b - x x ,
- 54. Итог урока
- 57. Задание на дом Найдите медиану и биссектрису большего угла треугольника АВС, если его стороны равны 4
- 58. Дополнительное задание.
- 59. Психологическая заминка Урок заканчивается, пожалуйста определите своё эмоциональное состояние в конце урока. Поставьте на этой же
- 61. Скачать презентацию

























 Взаимное расположение прямой и окружности. Взаимное расположение двух ркружностей.
Взаимное расположение прямой и окружности. Взаимное расположение двух ркружностей. Презентация учащихся
Презентация учащихся Презентация к интегрированному уроку геометрии по теме: Площади фигур
Презентация к интегрированному уроку геометрии по теме: Площади фигур Презентация по теме Цилиндр
Презентация по теме Цилиндр презентация к уроку геометрии Объем конуса
презентация к уроку геометрии Объем конуса Признаки параллельности прямых
Признаки параллельности прямых Четырехугольники
Четырехугольники Урок геометрии 7 класс Некоторые свойства прямоугольных треугольников
Урок геометрии 7 класс Некоторые свойства прямоугольных треугольников Презентация к уроку геометрии 8класс
Презентация к уроку геометрии 8класс Урок геометрии по темеТеорема Пифагора
Урок геометрии по темеТеорема Пифагора Презентация по теме Прямоугольные треугольники 7 класс учебник Атанасяна
Презентация по теме Прямоугольные треугольники 7 класс учебник Атанасяна Теорема Пифагора
Теорема Пифагора Презентация по теме Возникновение геометрии, 7 класс
Презентация по теме Возникновение геометрии, 7 класс Правильные многоугольники
Правильные многоугольники Заключительный урок по теме Четырехугольники
Заключительный урок по теме Четырехугольники Параллельные прямые
Параллельные прямые перпендикулярность прямой и плоскости.
перпендикулярность прямой и плоскости. Урок математики в 8 классе Площадь треугольника
Урок математики в 8 классе Площадь треугольника Объём шара. Площадь сферы.
Объём шара. Площадь сферы. Вертикальные и смежные углы
Вертикальные и смежные углы ПЛОЩАДИ ФИГУР
ПЛОЩАДИ ФИГУР Урок смотр знаний
Урок смотр знаний Классификация геометрических задач уровня С2 в Едином Государственном Экзамене с помощью программы “Живая математика” и метод координат в их решениях.
Классификация геометрических задач уровня С2 в Едином Государственном Экзамене с помощью программы “Живая математика” и метод координат в их решениях. кружковое занятие по геометрии
кружковое занятие по геометрии урок-обобщение по теме Многогранники
урок-обобщение по теме Многогранники презентация Из истории геометрических терминов
презентация Из истории геометрических терминов Смежные и вертикальные углы.7 класс.
Смежные и вертикальные углы.7 класс. план конспект урока по геометрии с использованием ЭОР
план конспект урока по геометрии с использованием ЭОР