Содержание
- 2. Лобачевского геометрия - геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия,
- 3. История создания геометрии Лобачевского одновременно является историей попыток доказать пятый постулат Евклида. Этот постулат представляет собой
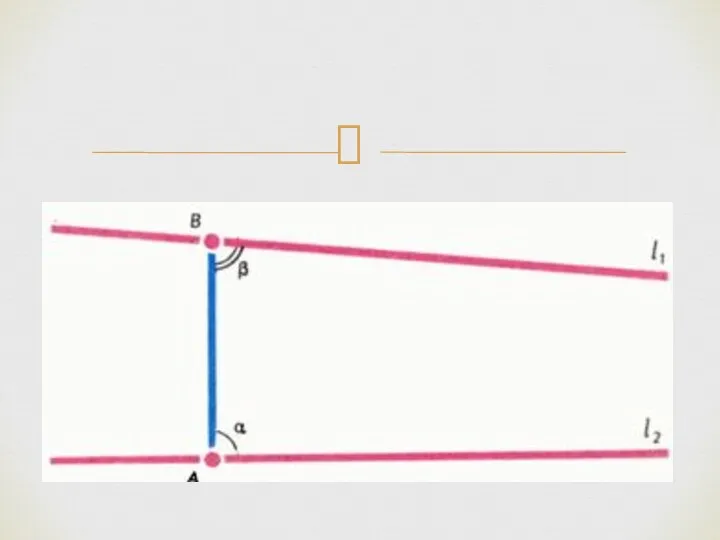
- 4. Например, если на рис. 1 угол – прямой, а угол чуть меньше прямого, то прямые и
- 6. Многие математики, жившие после Евклида, пытались доказать, что эта аксиома (пятый постулат) – лишняя, т.е. она
- 8. Критический анализ дальнейших попыток доказать пятый постулат выявил большое число аналогичных «очевидных» утверждений, которыми можно заменить
- 9. ) Через точку внутри угла, меньшего, чем развернутый, всегда можно провести прямую, пересекающую его стороны, т.е.
- 11. 2) Существуют два подобных треугольника, не равных между собой. 3) Три точки, расположенные по одну сторону
- 13. Постепенно «доказательства» становятся все изощреннее, в них все глубже прячутся малозаметные эквиваленты пятого постулата. Допустив, что
- 14. Первым, кто допустил возможность существования неевклидовой геометрии, в которой пятый постулат заменяется его отрицанием, был К.
- 15. XIX в. принес решение загадки пятого постулата. К этому открытию независимо от Гаусса пришел и наш
- 17. Рассказывая о геометрии Лобачевского, нельзя не отметить еще одного ученою, который вместе с Гауссом и Лобачевским
- 18. В геометрии Лобачевского сохраняются все теоремы, которые в евклидовой геометрии можно доказать без использования пятого постулата.Например:
- 19. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то в евклидовой геометрии равны
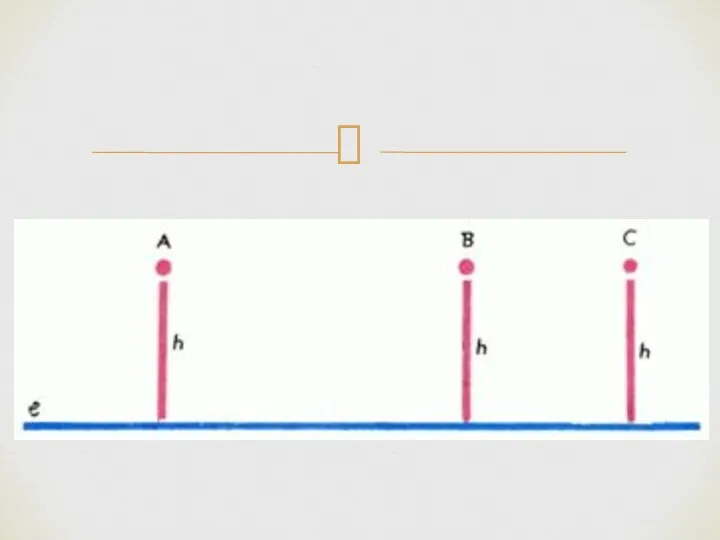
- 20. Разность между 180° и суммой углов треугольника ABC в геометрии Лобачевского положительна; она называется дефектом этого
- 21. Пусть теперь AOB – некоторый острый угол (рис. 5). В геометрии Лобачевского можно выбрать такую точку
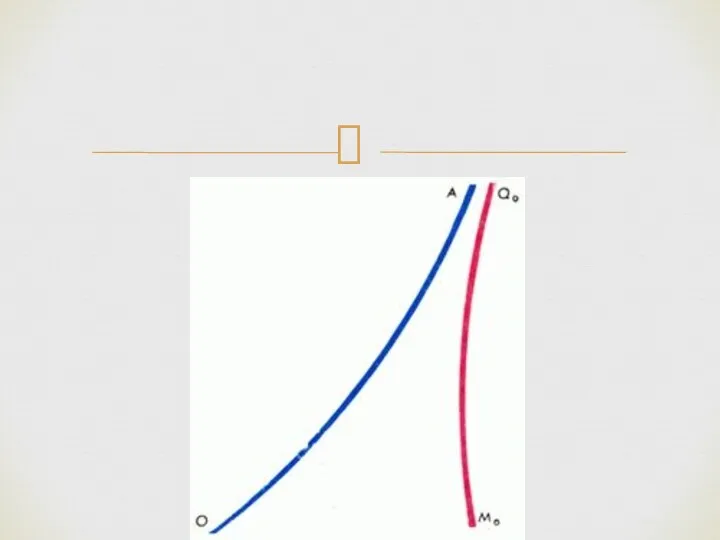
- 23. Прямые и все более приближаются друг к другу, но общих точек не имеют. На рис. 6
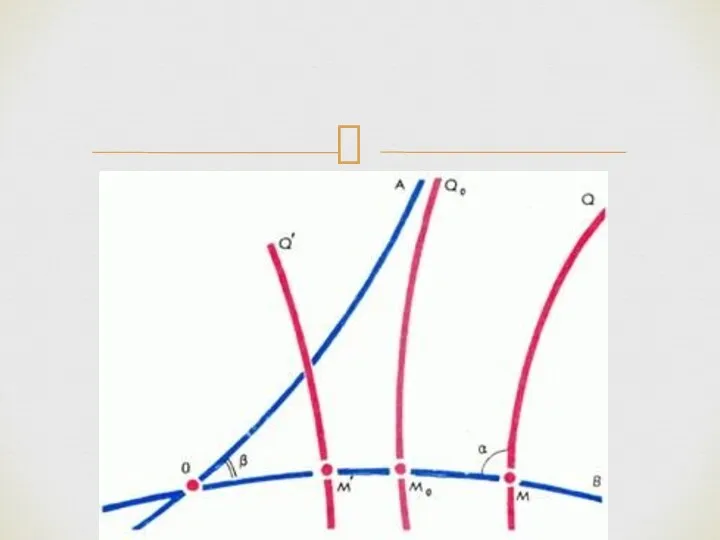
- 25. На рис. 7 перпендикуляр MQ к стороне OB угла AOB не пересекается со стороной AO, а
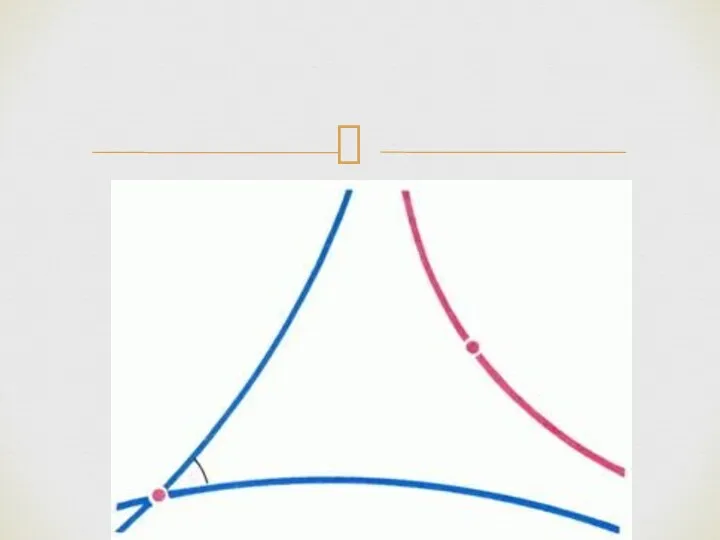
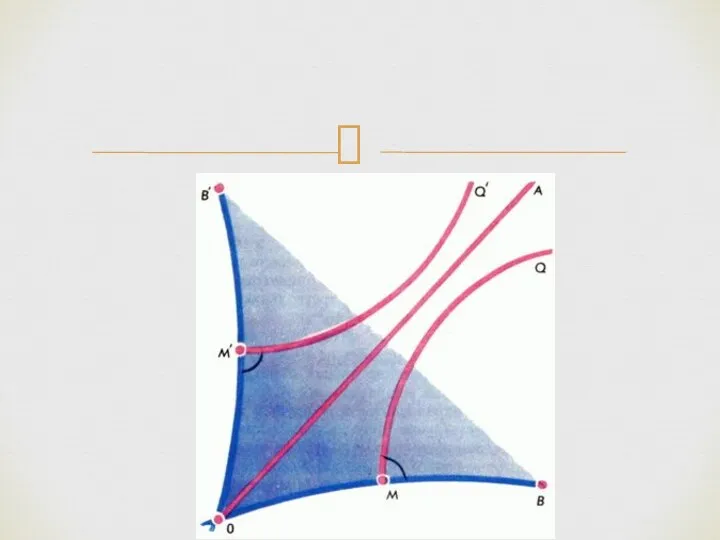
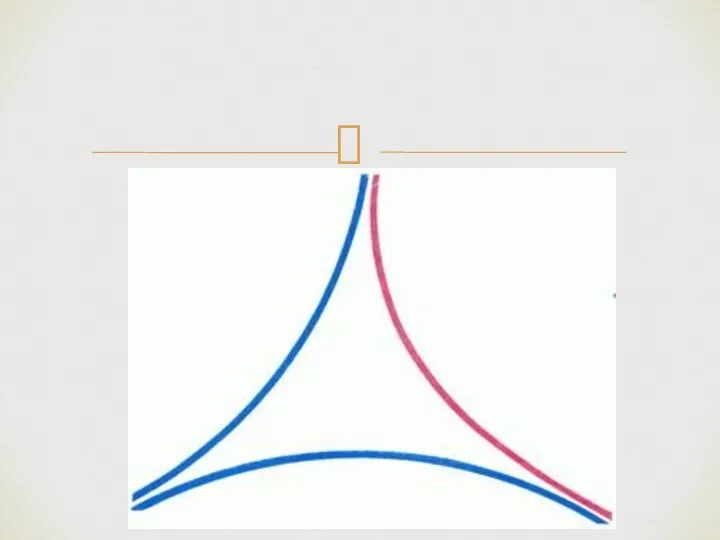
- 27. На рис. 8 изображен интересный вариант расположения трех прямых на плоскости Лобачевского: каждые две из них
- 30. НИКОЛАЙ ИВАНОВИЧ ЛОБАЧЕВСКИЙ (1792-1856)
- 31. С 14 лет жизнь Н.И.Лобачевского была связана с Казанским университетом. Его студенческие годы приходились на благополучный
- 32. Еще в первых числах февраля 1826 г. он передал в университет рукопись «Сжатое изложение начал геометрии
- 33. Ничто не могло поколебать уверенность Лобачевского в своей правоте. В течение 30 лет он продолжает развивать
- 34. 1) В Лобачевского геометрия не существует подобных, но неравных треугольников; треугольники равны, если их углы равны.
- 35. 2) Сумма углов всякого треугольника меньше p и может быть сколь угодно близкой к нулю. Это
- 36. 3) Через точку О, не лежащую на данной прямой а, проходит бесконечно много прямых, не пересекающих
- 37. 4) Если прямые имеют общий перпендикуляр, то они бесконечно расходятся в обе стороны от него. К
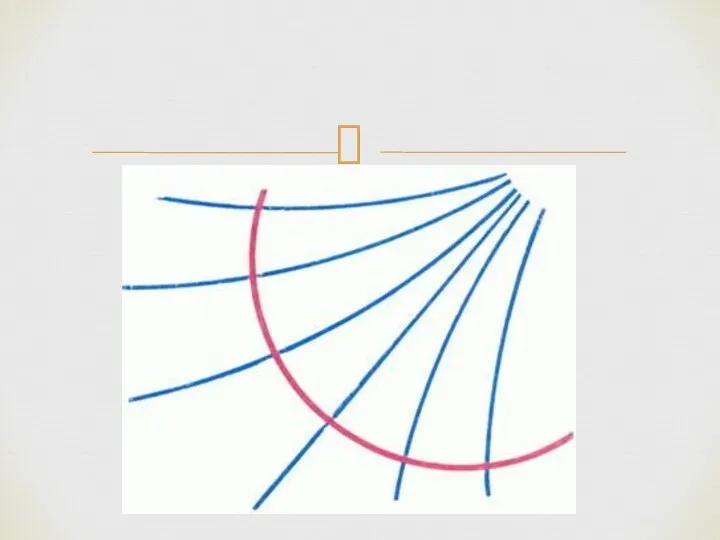
- 38. 7) Предел сфер бесконечно увеличивающегося радиуса не есть плоскость, а особая поверхность — предельная сфера, или
- 39. Лобачевского геометрия продолжает разрабатываться многими геометрами; в ней изучаются: решение задач на построение, многогранники, правильные системы
- 41. Скачать презентацию






























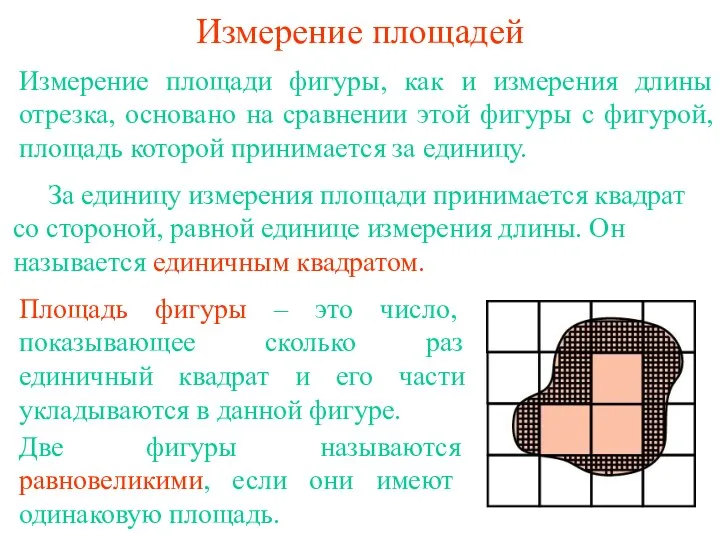 измерение площадей
измерение площадей Урок по теме Параллелепипед - 10 класс
Урок по теме Параллелепипед - 10 класс Определение параллельных прямых
Определение параллельных прямых Презентация к уроку Теорема Чевы
Презентация к уроку Теорема Чевы Презентация к уроку Изображение пространственных фигур на плоскости (10-11 классы)
Презентация к уроку Изображение пространственных фигур на плоскости (10-11 классы) Геометрические тела
Геометрические тела Пособие по решению заданий В3 и В6 в ЕГЭ
Пособие по решению заданий В3 и В6 в ЕГЭ Первый урок геометрии в 8 классе
Первый урок геометрии в 8 классе Презентация Прямой и развернутый угол
Презентация Прямой и развернутый угол Метод координат в пространстве
Метод координат в пространстве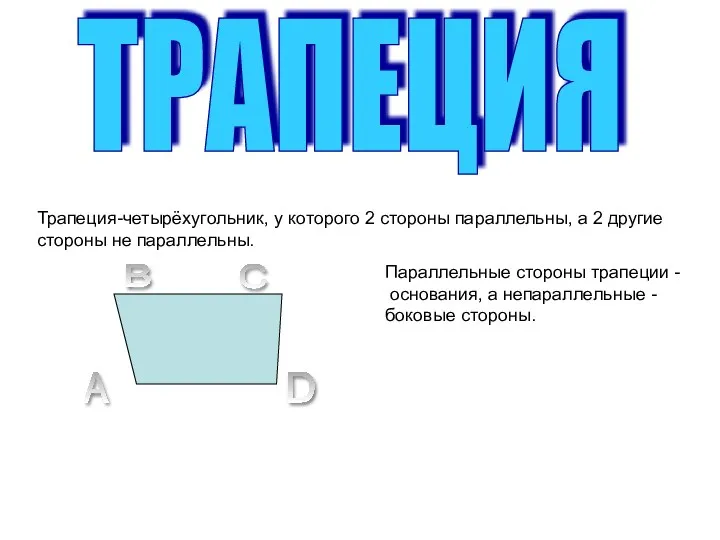 Урок-презентация по геометрии 8 класс на тему Трапеция
Урок-презентация по геометрии 8 класс на тему Трапеция Презентация Правильные многогранники
Презентация Правильные многогранники Методическая разработка урока по теме Медиана,биссектриса,высота треугольника
Методическая разработка урока по теме Медиана,биссектриса,высота треугольника презентация к уроку по геометрии 10 кл. Признак параллельности прямой и плоскости.
презентация к уроку по геометрии 10 кл. Признак параллельности прямой и плоскости. Некоторые свойства прямоугольных треугольников
Некоторые свойства прямоугольных треугольников Урок геометрии в 7 классе по теме Признаки параллельности прямых
Урок геометрии в 7 классе по теме Признаки параллельности прямых Повторение планиметрии.
Повторение планиметрии. Сумма углов треугольника
Сумма углов треугольника Сечения
Сечения презентация по теме цилиндр
презентация по теме цилиндр Интерактивный плакат по геометрии Признаки равенства треугольников 7 класс
Интерактивный плакат по геометрии Признаки равенства треугольников 7 класс Урок по теме Вычисление площадей фигур на клетчатой бумаге. Формула Пика.
Урок по теме Вычисление площадей фигур на клетчатой бумаге. Формула Пика. Урок на тему Аксиомы стереометрии
Урок на тему Аксиомы стереометрии урок-обобщение по теме Многогранники
урок-обобщение по теме Многогранники конспект урока по теме Многоугольники и презентация. 5 класс
конспект урока по теме Многоугольники и презентация. 5 класс Решение задач
Решение задач Презентация Построение сечений тетраэдра и параллелепипеда
Презентация Построение сечений тетраэдра и параллелепипеда Теорема о трех перпендикулярах(презентация)
Теорема о трех перпендикулярах(презентация)