Содержание
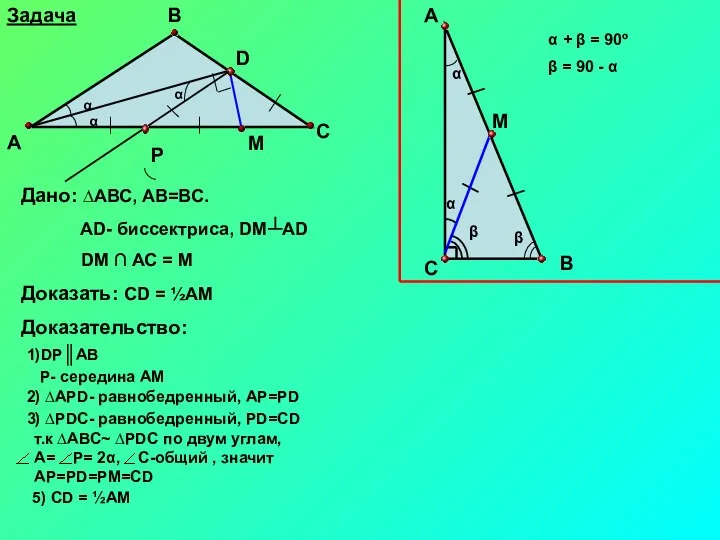
- 2. α + β = 90º β = 90 - α Дано: ∆АВС, АВ=ВС. AD- биссектриса, DM┴AD
- 3. II. CD = (BC · AC) / AB AC = (n² + m²) / n BC
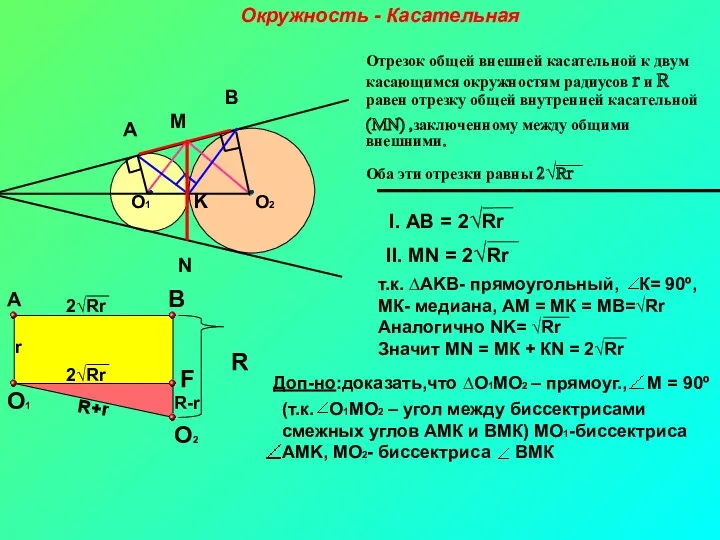
- 4. Окружность - Касательная
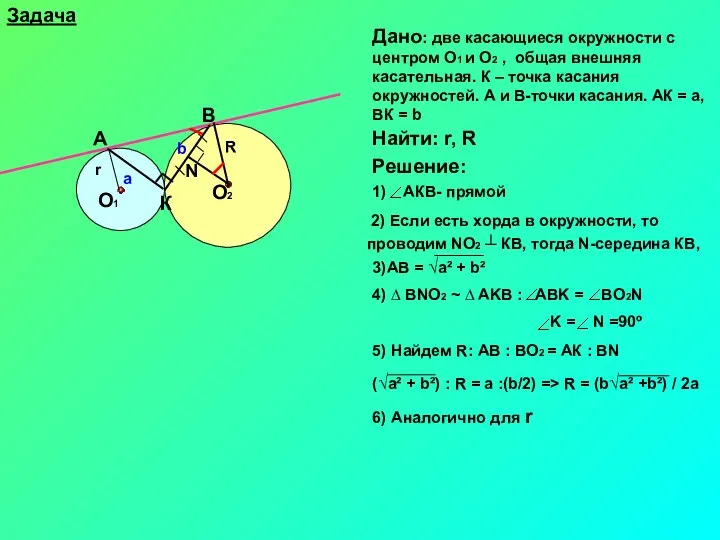
- 5. Задача
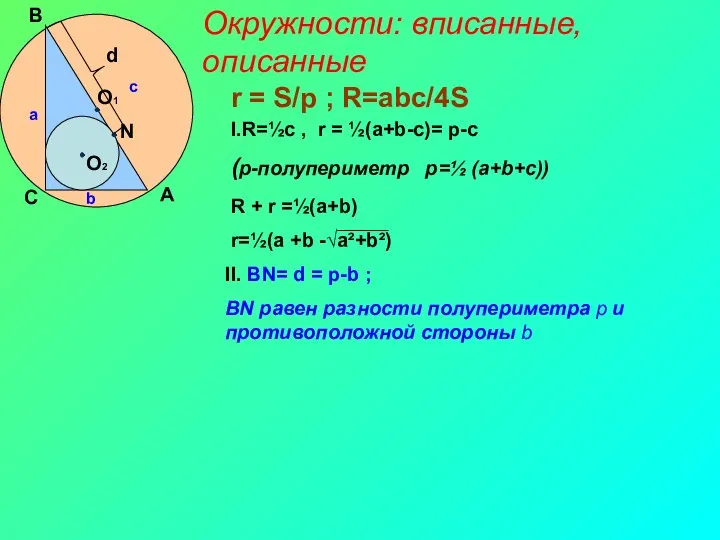
- 6. Окружности: вписанные, описанные I.R=½c , r = ½(a+b-c)= p-c (p-полупериметр p=½ (a+b+c)) r = S/p ;
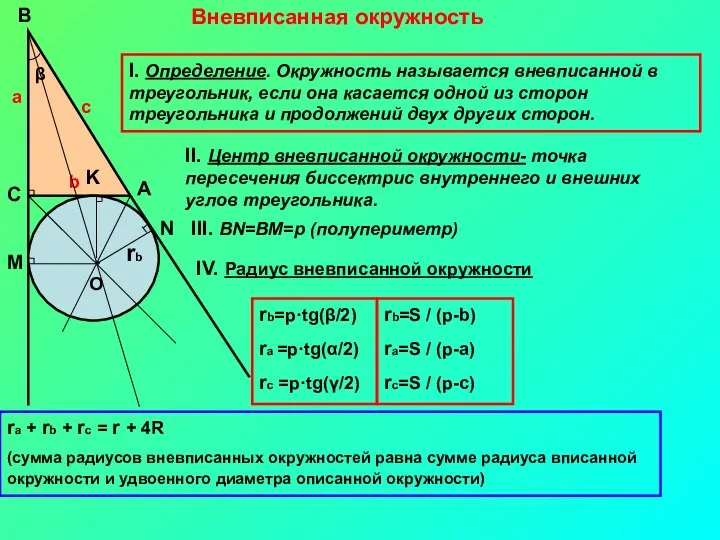
- 7. Вневписанная окружность I. Определение. Окружность называется вневписанной в треугольник, если она касается одной из сторон треугольника
- 9. Скачать презентацию

 Площадь треугольника
Площадь треугольника Презентация Двугранный угол
Презентация Двугранный угол Внеклассное мероприятие Геометрический съезд
Внеклассное мероприятие Геометрический съезд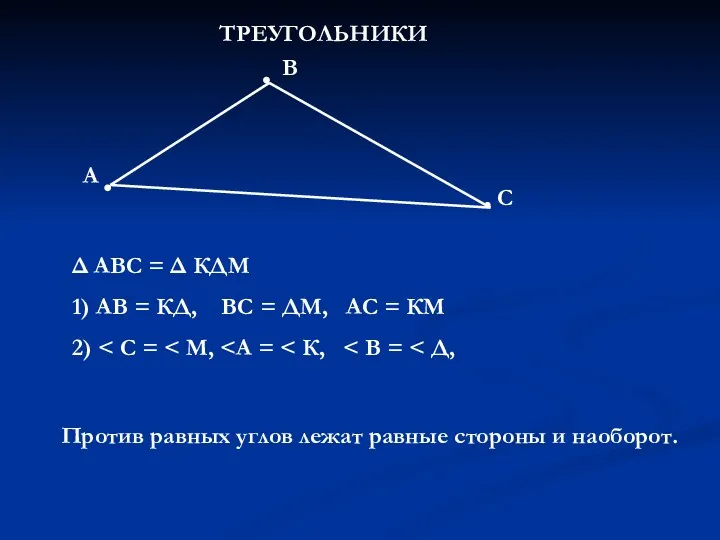 к уроку № 11 по геометрии 7 кл
к уроку № 11 по геометрии 7 кл Урок объяснения нового материала по геометрии в 10 классе. Тема: Параллельность прямой и плоскости
Урок объяснения нового материала по геометрии в 10 классе. Тема: Параллельность прямой и плоскости Сечения многогранников
Сечения многогранников к урокам 17-18 по геометрии 7 кл
к урокам 17-18 по геометрии 7 кл Теорема о существовании и единственности перпендикуляра
Теорема о существовании и единственности перпендикуляра Признаки равенства треугольников
Признаки равенства треугольников Урок на тему: Применение теоремы Пифагора.
Урок на тему: Применение теоремы Пифагора. Параллельные прямые
Параллельные прямые Конспект урока и презентация на тему Параллельные прямые, 7 класс
Конспект урока и презентация на тему Параллельные прямые, 7 класс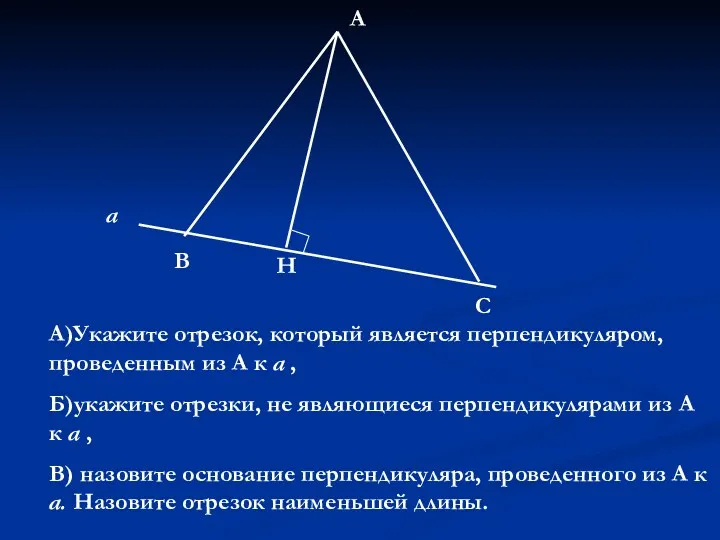 к урокам № 55-56 по геометрии 7 кл
к урокам № 55-56 по геометрии 7 кл Презентация Конструирование из кубиков
Презентация Конструирование из кубиков Биссектриса параллелограмма
Биссектриса параллелограмма Центральные и вписанные углы
Центральные и вписанные углы Правильные многоугольники (урок 2)
Правильные многоугольники (урок 2) Окружность и углы
Окружность и углы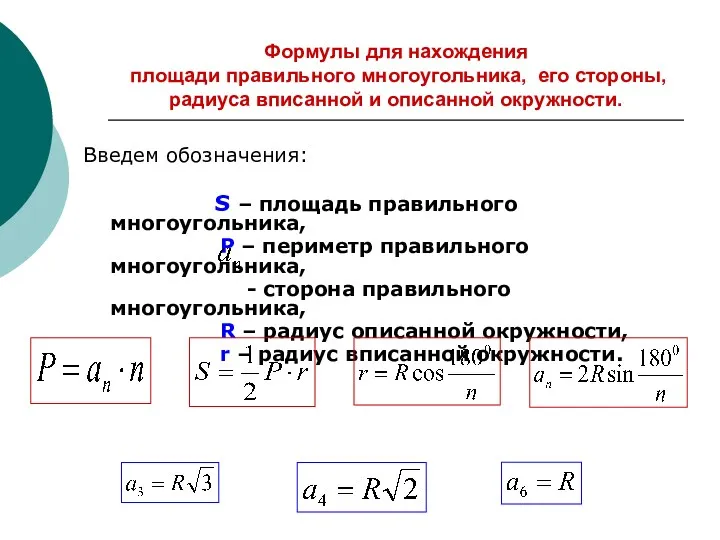 Презентация Площадь правильного многоугольника
Презентация Площадь правильного многоугольника начальное понятие треугольника
начальное понятие треугольника Презентация по геометрии по теме Сумма углов треугольника
Презентация по геометрии по теме Сумма углов треугольника Некоторые свойства прямоугольных треугольников
Некоторые свойства прямоугольных треугольников Презентация Треугольник
Презентация Треугольник Что изучает геометрия.
Что изучает геометрия. Простейшие задачи по теме Цилиндр и Конус
Простейшие задачи по теме Цилиндр и Конус Многогранники
Многогранники Урок по теме Сумма углов треугольника
Урок по теме Сумма углов треугольника Презентация к уроку Средняя линия
Презентация к уроку Средняя линия