Содержание
- 2. АФФИННЫЕ ПРЕОБРАЗОВАНИЯ 2.1. Преобразование координат Фундаментом компьютерной графики является аналитическая геометрия, и ее раздел - координатный
- 3. 2.1.1. Общие вопросы преобразования координат. Пусть задана n-мерная система координат, описывающая точку в пространстве, в базисе:
- 4. Обратное преобразование: По известным координатам:(m1, m2, …, mp) определить координаты (k1, k2, …, kn) k1 =
- 5. По системам координат - прямоугольная, полярная; преобразование из прямоугольной системы в полярную и наоборот. По виду
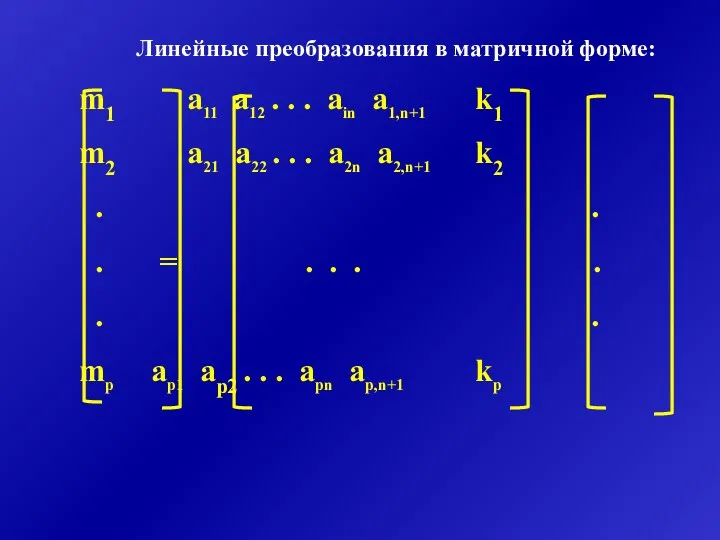
- 6. Линейные преобразования в матричной форме: m1 a11 a12 . . . ain a1,n+1 k1 m2 a21
- 7. Правила перемножения матриц: . . . . . . . . . . b1j . .
- 8. 2.2 Аффинные преобразования на плоскости На плоскости введена прямолинейная координатная система КС Каждой точке М ставится
- 9. Введя на плоскости еще одну прямоугольную систему координат, мы ставим в соответствие той же точке М
- 10. Запись аффинного преобразования в матричной форме: x’ A B C x y’ = D E F
- 11. Частные случаи аффинного преобразования 1. Параллельный сдвиг координат. 0 0 dx dy x y x' y'
- 12. 2. Растяжение-сжатие осей координат. 0 x x' y y' x' = x / kx y' =
- 13. 3. Поворот. • М α α 0 0 x x' y y' x y x' y'
- 14. Свойства аффинного преобразования: Любое аффинное преобразование может быть представлено как последовательность операций из числа последовательностей: сдвиг,
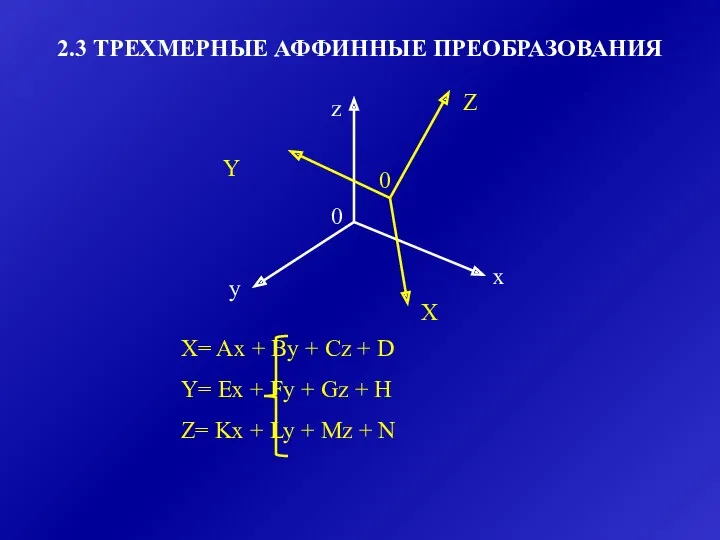
- 15. 2.3 ТРЕХМЕРНЫЕ АФФИННЫЕ ПРЕОБРАЗОВАНИЯ z y x Z X Y X= Ax + By + Cz
- 16. X= Ax + By + Cz + D Y= Ex + Fy + Gz + H
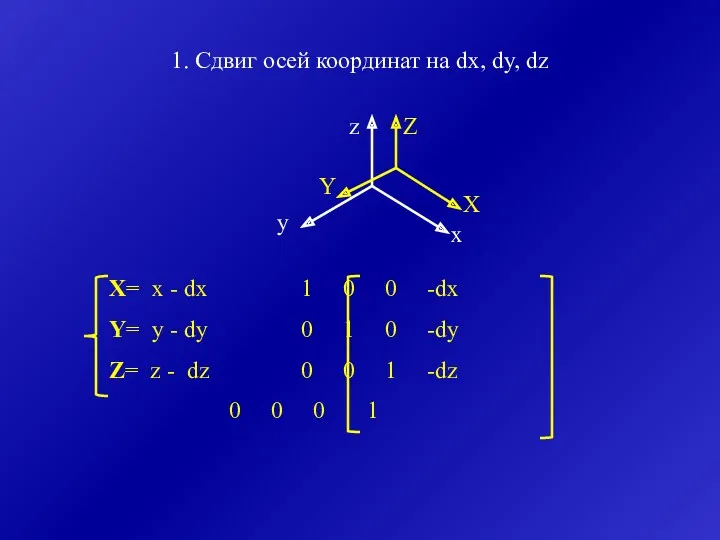
- 17. X= x - dx 1 0 0 -dx Y= y - dy 0 1 0 -dy
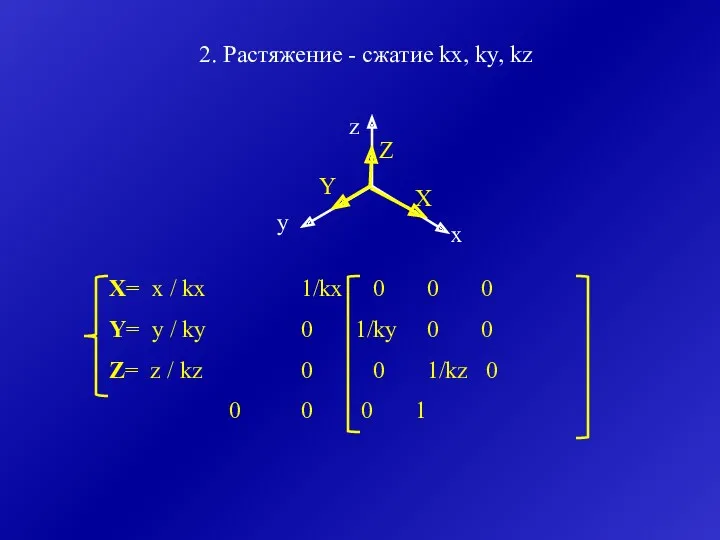
- 18. X= x / kx 1/kx 0 0 0 Y= y / ky 0 1/ky 0 0
- 19. X= x 1 0 0 0 Y= y cos ϕ - z sin ϕ 0 cos
- 20. X= x cos ς - z sin ς cos ς 0 -sin ς 0 Y= y
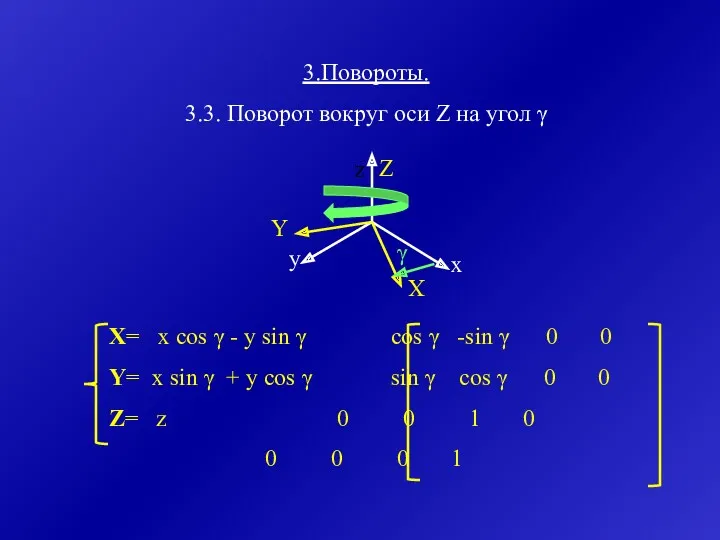
- 21. X= x cos γ - y sin γ cos γ -sin γ 0 0 Y= x
- 22. ПРЕОБРАЗОВАНИЯ ОБЪЕКТОВ Исходные данные: n-мерная система координат. Координаты точки: (K1, K2, …. Kn). Новое положение точки:
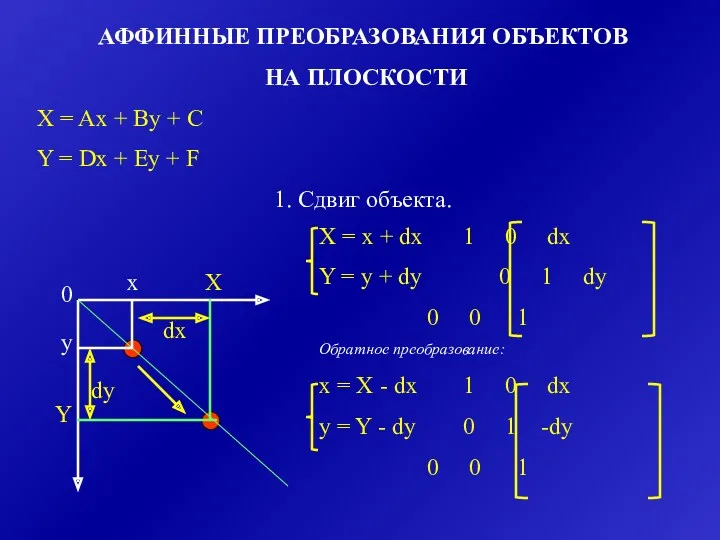
- 23. АФФИННЫЕ ПРЕОБРАЗОВАНИЯ ОБЪЕКТОВ НА ПЛОСКОСТИ X = Ax + By + C Y = Dx +
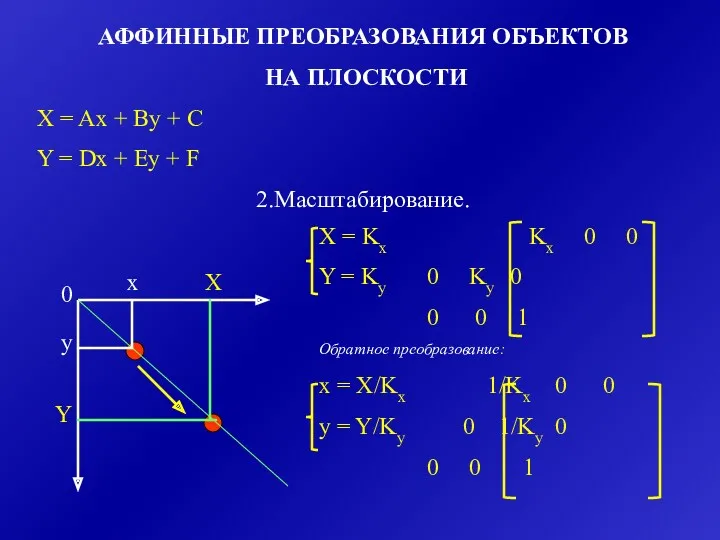
- 24. АФФИННЫЕ ПРЕОБРАЗОВАНИЯ ОБЪЕКТОВ НА ПЛОСКОСТИ X = Ax + By + C Y = Dx +
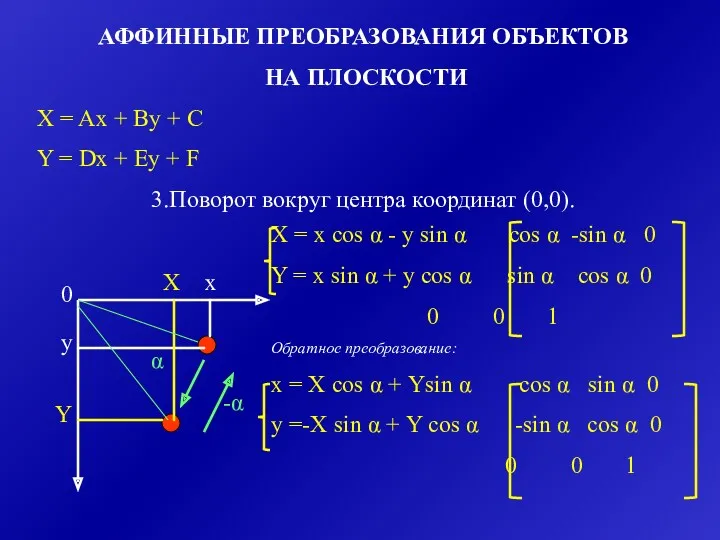
- 25. АФФИННЫЕ ПРЕОБРАЗОВАНИЯ ОБЪЕКТОВ НА ПЛОСКОСТИ X = Ax + By + C Y = Dx +
- 26. АФФИННЫЕ ПРЕОБРАЗОВАНИЯ ОБЪЕКТОВ В ПРОСТРАНСТВЕ (3-х мерное преобразование) X = Ax + By + Cz +
- 27. АФФИННЫЕ ПРЕОБРАЗОВАНИЯ ОБЪЕКТОВ В ПРОСТРАНСТВЕ (3-х мерное преобразование) X = Ax + By + Cz +
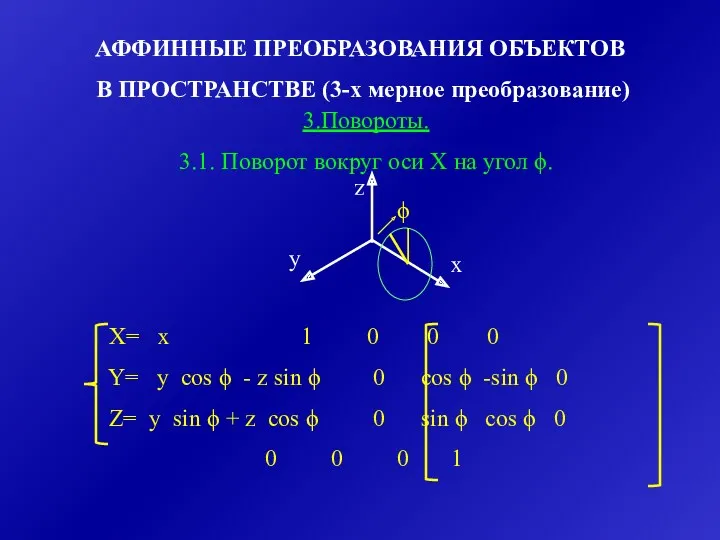
- 28. АФФИННЫЕ ПРЕОБРАЗОВАНИЯ ОБЪЕКТОВ В ПРОСТРАНСТВЕ (3-х мерное преобразование) X= x 1 0 0 0 Y= y
- 29. АФФИННЫЕ ПРЕОБРАЗОВАНИЯ ОБЪЕКТОВ В ПРОСТРАНСТВЕ (3-х мерное преобразование) X= x cos ς - z sin ς
- 30. АФФИННЫЕ ПРЕОБРАЗОВАНИЯ ОБЪЕКТОВ В ПРОСТРАНСТВЕ (3-х мерное преобразование) X= x cos γ - y sin γ
- 31. СВЯЗЬ ПРЕОБРАЗОВАНИЙ ОБЪЕКТОВ С ПРЕОБРАЗОВАНИЯМИ КООРДИНАТ. α 0 x0 y0 x X y 0' Y', y'
- 32. СВЯЗЬ ПРЕОБРАЗОВАНИЙ ОБЪЕКТОВ С ПРЕОБРАЗОВАНИЯМИ КООРДИНАТ. Объединив формулы: x'=x-x0 X'=x'cosα-y'sinα X = X' + x0 y'=y-y0
- 34. Скачать презентацию






















 Program NN1
Program NN1 Использование двоичной и шестнадцатеричной систем счисления
Использование двоичной и шестнадцатеричной систем счисления Сравнительный анализ дизайна сайтов
Сравнительный анализ дизайна сайтов Управление памятью
Управление памятью Внедрение 3D технологий. Трехмерная графика
Внедрение 3D технологий. Трехмерная графика Кодирование и декодирование информации
Кодирование и декодирование информации Развитие детей с помощью курсов робототехники
Развитие детей с помощью курсов робототехники Диспетчер задач Windows
Диспетчер задач Windows Арифметические и логические основы компьютера. (Лекция1-2)
Арифметические и логические основы компьютера. (Лекция1-2) СТС. Осень 2016
СТС. Осень 2016 Внеклассное мероприятие Путешествие информатиков весёлых и находчивых
Внеклассное мероприятие Путешествие информатиков весёлых и находчивых Влияние личности игрока на развитие сюжета в играх с несколькими концовками
Влияние личности игрока на развитие сюжета в играх с несколькими концовками Configure a Switch
Configure a Switch Windows 10
Windows 10 Оценка юзабилити
Оценка юзабилити Компьютер – инструмент подготовки текстов
Компьютер – инструмент подготовки текстов Логические операторы. Операторы сравнения. Тернарный оператор
Логические операторы. Операторы сравнения. Тернарный оператор Использование информационно-коммуникационных технологий на уроках технологии
Использование информационно-коммуникационных технологий на уроках технологии Типовая схема организации связи цифровой сети МО РФ
Типовая схема организации связи цифровой сети МО РФ Контроль пропускної здатності корпоративної комп'ютерної мережі засобами NMS моделі ISO
Контроль пропускної здатності корпоративної комп'ютерної мережі засобами NMS моделі ISO Практическое занятие по робототехнике
Практическое занятие по робототехнике Тема алгоритмизация и программирование относится к общеобразовательному уровню в 9 классах.
Тема алгоритмизация и программирование относится к общеобразовательному уровню в 9 классах. Електронне листування з використанням веб-інтерфейсу. Вкладені файли
Електронне листування з використанням веб-інтерфейсу. Вкладені файли Динамические структуры данных. Указатели
Динамические структуры данных. Указатели Коллекции в Java
Коллекции в Java Составление рограммы, используя условный оператор
Составление рограммы, используя условный оператор Применение технологии Web 2.0 в библиотеках
Применение технологии Web 2.0 в библиотеках Трассировка контура
Трассировка контура