Содержание
- 2. Алгоритм Бойера-Мура 1. Правило «плохого символа». P 1 1 m i+1 i+m T T P P
- 3. Алгоритм Бойера-Мура 2. Правило «хорошего cуффикса». P 1 1 m i+1 i+m T P y x
- 4. Поиск образцов. Алгоритм Shift-And Пример. Пусть Σ = {a,b,c}, p=aabac, T=aabaacaabacab. R[m, j] = 1: P
- 5. Алгоритм Shift-And Пример. Пусть Σ = {a,b,c}, p=aabac, T=aabaacaabacab. Переход от j-го столбца R к (j+1)-му:
- 6. Алгоритм Shift-And Пример. Пусть Σ = {a,b,c}, p=aabac, T=aabaacaabacab. Схема перехода от 3-го столбца R к
- 7. Алгоритм Карпа-Рабина ns : Σ → [0.. |Σ| - 1] - порядок символов в Σ. Пусть
- 8. Обобщения задачи поиска образца: Образцы с джокерами: x – любой символ Пример. P = abxxcx содержится
- 9. Алгоритм Ахо-Корасик Задача. Задано множество образцов P = {P1, P2, … Pz}. Требуется обнаружить все вхождения
- 10. Алгоритм Ахо-Корасик Этап предобработки: построение ДКА по исходному множеству образцов Этап поиска: однократный "прогон" текста через
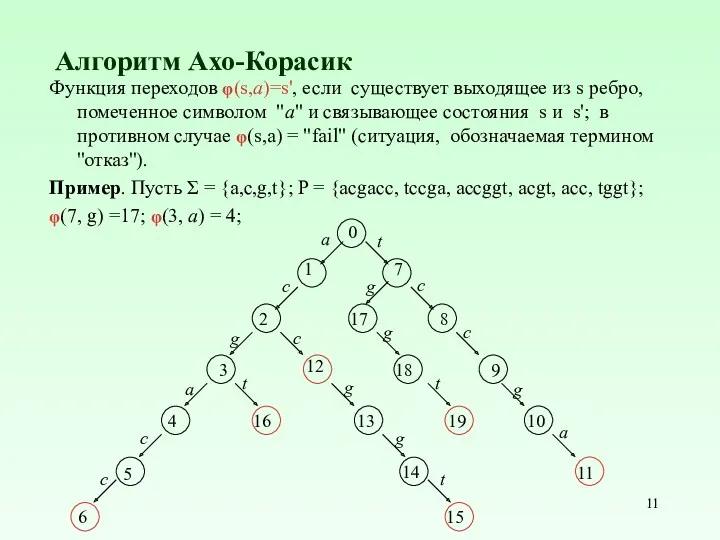
- 11. Алгоритм Ахо-Корасик Функция переходов φ(s,a)=s', если существует выходящее из s ребро, помеченное символом "a" и связывающее
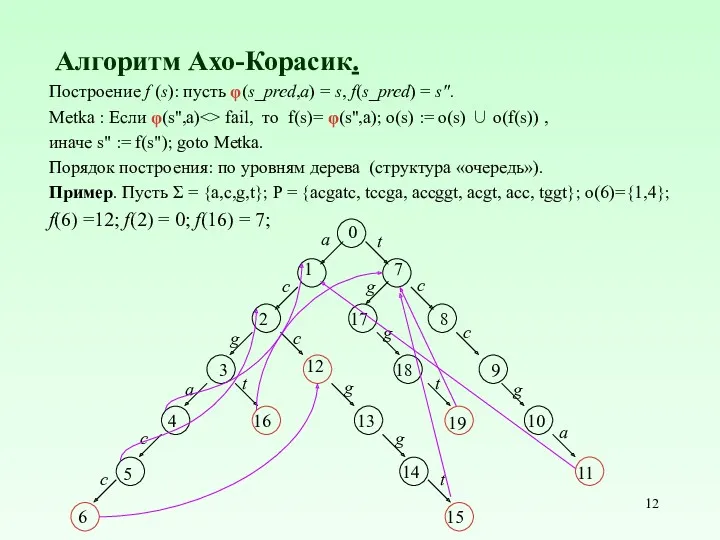
- 12. Алгоритм Ахо-Корасик. Построение f (s): пусть φ(s_pred,a) = s, f(s_pred) = s". Metka : Если φ(s'',a)
- 14. Скачать презентацию





![Алгоритм Карпа-Рабина ns : Σ → [0.. |Σ| - 1]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/258157/slide-6.jpg)



 Презентация по теме Кодирование информации 3 класс
Презентация по теме Кодирование информации 3 класс Базовые приемы для бизнеса. Возможности Вашего аккаунта
Базовые приемы для бизнеса. Возможности Вашего аккаунта WI-FI технологиясы
WI-FI технологиясы Сравнительный анализ дизайна интернет-сайтов
Сравнительный анализ дизайна интернет-сайтов Молодіжний комп'ютерний сленг
Молодіжний комп'ютерний сленг Инструкция по созданию интерактивных физкультминуток
Инструкция по созданию интерактивных физкультминуток TMS для транспортных компаний
TMS для транспортных компаний Компьютерлік вирустар. Архиваторлар
Компьютерлік вирустар. Архиваторлар Безпека в інтернеті
Безпека в інтернеті Система станционной телемеханики
Система станционной телемеханики Векторная графика
Векторная графика Язык программирования Python
Язык программирования Python Сетевой этикет
Сетевой этикет Задача линейного программирования и способы решения
Задача линейного программирования и способы решения Операционная система
Операционная система Отчет по лабораторным работам за семестр, по дисциплине:”Информатика”
Отчет по лабораторным работам за семестр, по дисциплине:”Информатика” Точка отсчета. Интернет-игра нового поколения
Точка отсчета. Интернет-игра нового поколения Математическая модель, алгоритм 1 урок
Математическая модель, алгоритм 1 урок Интернет-технологии в социальной работе
Интернет-технологии в социальной работе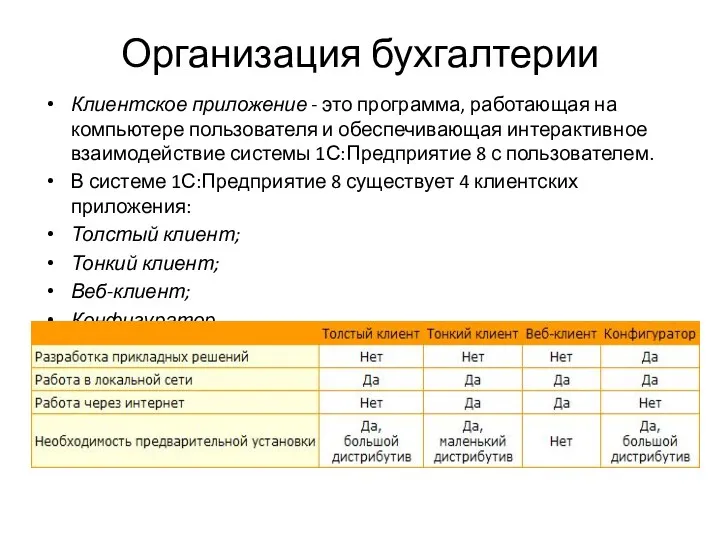 Организация бухгалтерии. Клиентское приложение
Организация бухгалтерии. Клиентское приложение Доступы: гостевой и представительский доступ, настройка и управление
Доступы: гостевой и представительский доступ, настройка и управление Тема Кодирование графической информации
Тема Кодирование графической информации Построение таблиц истинности
Построение таблиц истинности Телекоммуникационные технологии
Телекоммуникационные технологии Моделирование как метод познания
Моделирование как метод познания Моделирование в Blender 3D
Моделирование в Blender 3D Виртуальное моделирование химических процессов
Виртуальное моделирование химических процессов Функции в Python
Функции в Python