Содержание
- 2. В первой половине XII века книга аль-Хорезми в латин-ском переводе проникла в Европу. Переводчик дал ей
- 3. Например, алгоритм – процедура, состоящая из “конеч-ного числа команд, каждая из которых выполняется меха-нически за фиксированное
- 4. В формальных описаниях алгоритм конструктивно связы-вают с понятием машины, предназначенной для автома-тизированных преобразований символьной информации. Для
- 5. Подобными моделями алгоритмических преобразований символьной информации являются: - конечные автоматы; - машина Тьюринга; - машина Поста;
- 6. РЕГУЛЯРНЫЕ ЯЗЫКИ Для того, чтобы представить формальное описание алго-ритма необходимо формальное описание решаемой зада-чи. В большинстве
- 7. К сожалению, теория алгоритмов не дает и не может дать как универсального, формального способа описания зада-чи,
- 8. Алфавит языка обозначается как конечное множество символов. Например: Σ={a,b,c,d}, Σ={0,1}. Символ и цепочка символов образуют слово
- 9. 1) Символы алфавита могут соединяться конкатенацией (сцепление, соединение) в цепочки символов-слов, кото-рые соединяются в новые слова.
- 10. 2) объединение (S1 ∪S2) или (S1+ S2) множеств S1={a, aa, ba}, S2={e, bb, ab}, S1 ∪
- 11. Формулы, содержащие эти операции с множествами слов, называют регулярными выражениями. Дистрибутивность объединения с итерацией S1 *(S2
- 12. Пример. Регулярные выражения регулярного языка в алфавите Σ ={0,1} (0 ∪(1(0)*)) = 0 ∪ 10*; (0
- 13. Примеры правильных арифметических выражений i , - i , i + i , i - i
- 14. Определение. Конечный автомат определяется символами M=(Q, Σ, δ, q0, F), где Q={q0, q1, …, qn} –
- 15. КА называется детерминированным (ДКА), если Pj содержит не более одного состояния. КА полностью определенный, если Pj
- 16. а КА читает входной символ в текущем состоянии qi ∈ Q, переходит в следующее состояние qj
- 17. k = (q, ω) текущая конфигурация; k0 = (q 0, ω0) начальная конфигурация; kf = (q,
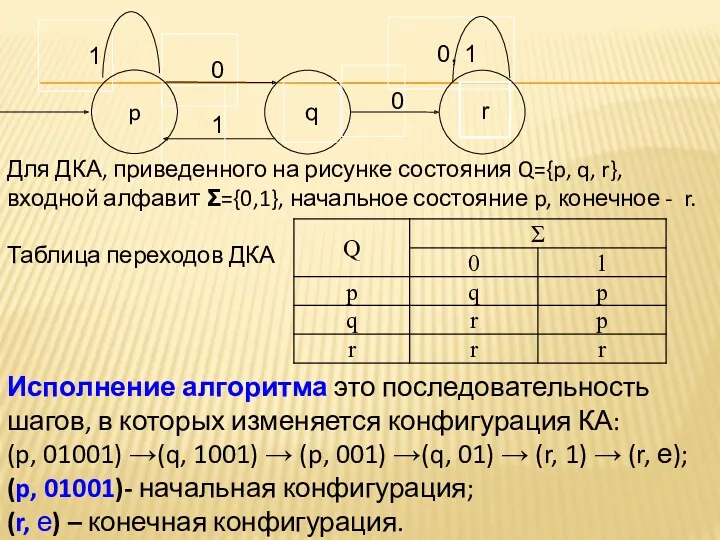
- 18. Для ДКА, приведенного на рисунке состояния Q={p, q, r}, входной алфавит Σ={0,1}, начальное состояние p, конечное
- 19. В результате применения слова 01001 в начальном состоянии p автомат переходит в следующее состояние q и
- 20. МАШИНА ТЬЮРИНГА Универсальный КА, применяемый для решения любой алгоритмически разрешимой задачи, в теории алгоритмов и вычислений
- 21. При чтении очередного символа с ленты выполняется определенная команда K, автомат переходит в следующее состояние и
- 22. Машина Тьюринга имеет фундаментальное значение в теории алгоритмов как формальное определение алго-ритма в строгой и точной
- 23. Поэтому задача сводится к частной и более простой зада-че, для которой можно доказать, что соответствующей машины
- 24. Функция вычислима, если существует алгоритм – эффек-тивная последовательная процедура вычисления от простого к сложному. Выделяется базис
- 25. К элементарным вычислимым функциям относятся: 1) S(x) = x+1 - следование – вычисление следующего натурального числа;
- 26. Утверждение. Всякая рекурсивная функция эффективно вычислима – существует метод, который по рекурсивному описанию строит алгоритм вычисления
- 27. 2. Произведение - вычисляется Ф(x, C) = x * C для заданного множителя x Ф(0, C)
- 28. На практике рекурсивное описание задач является тру-доемким и интуитивным, вместе с тем уровень сложности решаемых задач
- 29. 2. Ряд чисел Фибоначчи F1, F2,…, Fn: Трасса строится по рекуррентной формуле Fn=Fn-1 +Fn-2, n ≥2;
- 30. 4. Степенные ряды и полиномы. Широко используются в виде производящих функций, в приближениях функций рядами Тейлора,
- 31. КЛАССЫ СЛОЖНОСТИ В рамках классической теории алгоритмические задачи различаются по классам сложности (P-сложные, NP-сложные, экспоненциально сложные
- 32. В качестве ресурсов обычно берутся время вычисления (количество рабочих тактов машины Тьюринга) или рабочая зона (количество
- 33. К классу NP относятся задачи, решение которых с помощью дополнительной информации полиномиальной длины, данной нам свыше,
- 34. Поскольку класс P содержится в классе NP, принадлеж-ность той или иной задачи к классу NP зачастую
- 35. Наиболее часто встречающиеся классы сложности в зависимости от числа входных данных n таковы: О(1) - количество
- 36. Сложность О(nlog2n) имеют алгоритмы быстрой сортиров-ки, сортировки слиянием и "кучной" сортировки, алго-ритм Краскала - построение минимального
- 37. Алгоритм показывает кубическое время, если его поря-док равен О(n3), и такие алгоритмы очень медленные. Всякий раз,
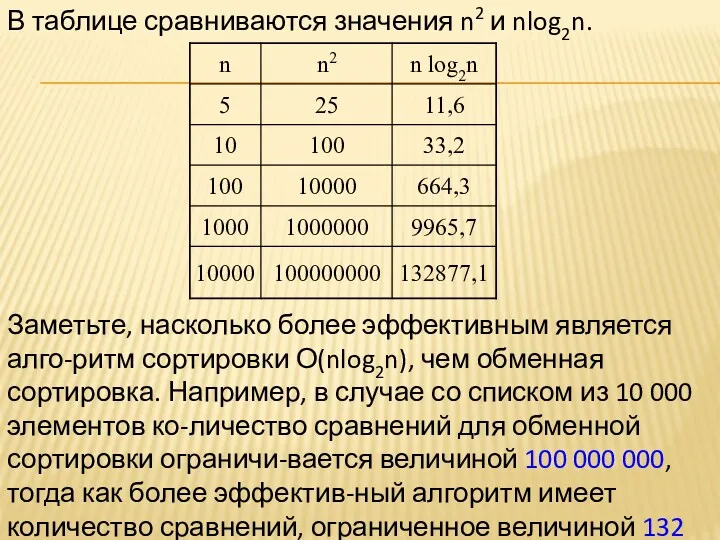
- 38. В таблице сравниваются значения n2 и nlog2n. Заметьте, насколько более эффективным является алго-ритм сортировки О(nlog2n), чем
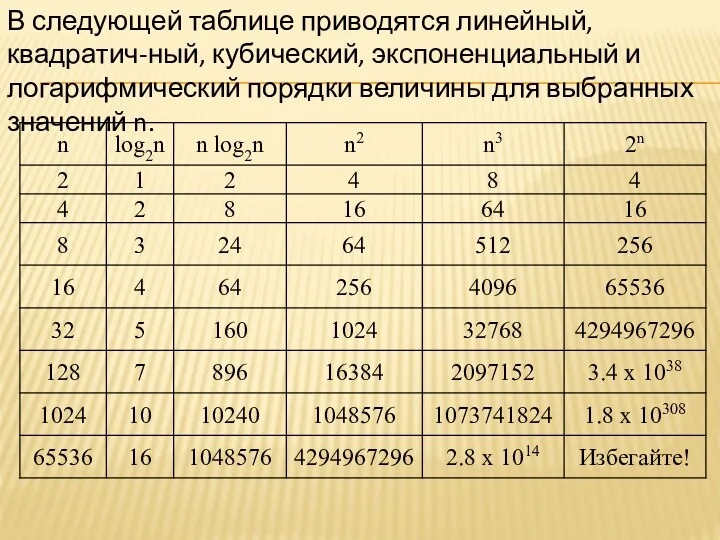
- 39. В следующей таблице приводятся линейный, квадратич-ный, кубический, экспоненциальный и логарифмический порядки величины для выбранных значений n.
- 40. Из таблицы очевидно, что следует избегать использования кубических и экспоненциальных алгоритмов, если только значение n не
- 41. Эти примеры показывают, что, выбирая ЭВМ в К раз более быстро-действующую, получаем увеличение размера решаемых задач
- 43. Скачать презентацию





































 Організація і функціонування інтерфейсів паралельних КС. (Тема 16)
Організація і функціонування інтерфейсів паралельних КС. (Тема 16) Использование информационных технологий в образовательном процессе
Использование информационных технологий в образовательном процессе Общие сведения о системах связи. Математические модели сообщений сигналов и помех
Общие сведения о системах связи. Математические модели сообщений сигналов и помех Сетевые экраны
Сетевые экраны Основы объектно-ориентированного программирования
Основы объектно-ориентированного программирования Архитектуры удалённых баз данных
Архитектуры удалённых баз данных Мастер по обработке цифровой информации
Мастер по обработке цифровой информации Групповая разработка телеграм-бота Помощник в поиске тренера по бегу
Групповая разработка телеграм-бота Помощник в поиске тренера по бегу Размеры. Нанесение размеров (часть 2)
Размеры. Нанесение размеров (часть 2) Создание поверхностных моделей
Создание поверхностных моделей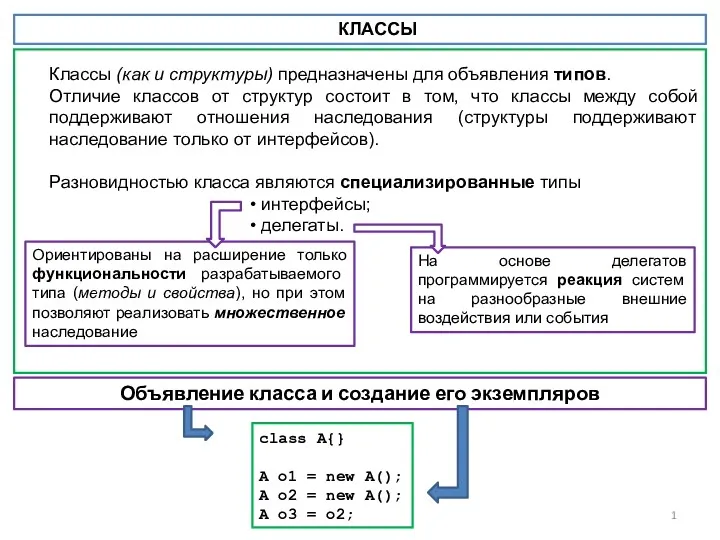 Классы. Основные понятия
Классы. Основные понятия Таргетолог и smm-специалист
Таргетолог и smm-специалист Необобщенные коллекции
Необобщенные коллекции Презентация Профессии, по которым необходимы знания по программе Microsoft Access
Презентация Профессии, по которым необходимы знания по программе Microsoft Access HDD - плата управления
HDD - плата управления Файлы и файловые структуры. Компьютер как универсальное устройство для работы с информацией. Информатика. 7 класс
Файлы и файловые структуры. Компьютер как универсальное устройство для работы с информацией. Информатика. 7 класс Сети TD-LTE: Перспективы, особенности построения и операторской деятельности в России
Сети TD-LTE: Перспективы, особенности построения и операторской деятельности в России Современные компьютерные технологии. (Modern Computer technologies)
Современные компьютерные технологии. (Modern Computer technologies) Using objects in JavaScript. Accessing DOM in JavaScript
Using objects in JavaScript. Accessing DOM in JavaScript Гипертекст как модель организации поисковых систем
Гипертекст как модель организации поисковых систем SQL (Structured Query Language). Структурированный язык запросов
SQL (Structured Query Language). Структурированный язык запросов Правила безопасности в компьютерном классе
Правила безопасности в компьютерном классе Domain valuation result page
Domain valuation result page Всемирная паутина, поисковые системы
Всемирная паутина, поисковые системы Итоговый тест. 5 класс
Итоговый тест. 5 класс Множества. Массивы (Delphi)
Множества. Массивы (Delphi) Базы данных. Основные понятия
Базы данных. Основные понятия Накопители информации
Накопители информации