- Главная
- Информатика
- Дерево отрезков

Содержание
- 2. Строим дерево отрезков Пусть у нас есть массив b из n элементов. Для начала нам нужно
- 3. Далее нужно заполнить массив a нулями (соответствующего типа) и заполнить листы ДО значениями из массива b
- 4. Узнать значение i-го элемента. Как уже писалось ранее у нашего ДО листья имеют индексы от nMax
- 5. Изменить значение i-го элемента. Если мы изменим значение в листе дерева, то все значения на пути
- 6. Теперь осталось подняться до корня, это можно сделать с помощью цикла: while (i>1) { i/= 2;
- 7. Найти значение функции на отрезке от l до r. Наконец-то, мы добрались до самого интересного запроса.
- 8. Для того, что бы вычислить значение функции на отрезке, нам необходимо разбить его на МИНИМАЛЬНОЕ количество
- 9. Создаем вспомогательную функцию. int query(int l, int r, int leftPosition, int rightPosition, int v) { //
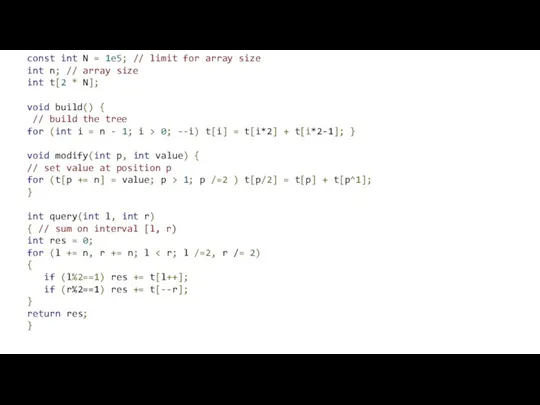
- 10. const int N = 1e5; // limit for array size int n; // array size int
- 12. Скачать презентацию
Слайд 2
Строим дерево отрезков
Пусть у нас есть массив b из n элементов.
Строим дерево отрезков
Пусть у нас есть массив b из n элементов.
Для начала нам нужно найти nMax (наименьшая степень двойки, которая не превосходит n). Это можно реализовать как через формулу:
nMax = 2* ((int)(log2(1.0*(n-1)) + 1);
Или вот так
nMax= 1;
while (nMax
nMax = 2* ((int)(log2(1.0*(n-1)) + 1);
Или вот так
nMax= 1;
while (nMax
Слайд 3
Далее нужно заполнить массив a нулями (соответствующего типа) и заполнить листы
Далее нужно заполнить массив a нулями (соответствующего типа) и заполнить листы
ДО значениями из массива b (мы помним, что в ДО индексы листьев от nMax до 2*nMax-1):
for (int i=0; i a[nMax+i]= b[i];
Теперь осталось только заполнить значения во всех родителях. Это можно сделать за один линейный проход (помним, что у i-ой вершины сыновья с индексами 2*i и 2*i+1, а в вершине мы храним значение функции от двух сыновей):
for (int i=nMax-1; i>0; i--)
a[i]= f(a[2*i],a[2*i+1]);
Таким образом мы построили ДО с асимптотикой O(nMax) = O(n).
В нашем случае мы будем считать, что a[0] не участвует в дереве отрезков.
А корень располагается в a[1].
for (int i=0; i
Теперь осталось только заполнить значения во всех родителях. Это можно сделать за один линейный проход (помним, что у i-ой вершины сыновья с индексами 2*i и 2*i+1, а в вершине мы храним значение функции от двух сыновей):
for (int i=nMax-1; i>0; i--)
a[i]= f(a[2*i],a[2*i+1]);
Таким образом мы построили ДО с асимптотикой O(nMax) = O(n).
В нашем случае мы будем считать, что a[0] не участвует в дереве отрезков.
А корень располагается в a[1].
Слайд 4
Узнать значение i-го элемента.
Как уже писалось ранее у нашего ДО листья
Узнать значение i-го элемента.
Как уже писалось ранее у нашего ДО листья
имеют индексы от nMax до 2*nMax-1, поэтому значение i-го элемента находиться в ячейке с индексом nMax+i:
return a[nMax+i]
Очевидно, что данный запрос выполняется за константу.
return a[nMax+i]
Очевидно, что данный запрос выполняется за константу.
Слайд 5
Изменить значение i-го элемента.
Если мы изменим значение в листе дерева, то
Изменить значение i-го элемента.
Если мы изменим значение в листе дерева, то
все значения на пути к корню от данного листа перестанут соответствовать действительности, поэтому их нужно пересчитать, в остальных же останутся корректные значения.
Как известно, глубина полного бинарного дерева из m вершин равна log2m, поэтому мы должны выполнить данную операцию за логарифмическое время. Например, изменим a2 на a2I :
Что бы «обновить» ДО нам нужно записать в лист новое значение, а затем подняться до корня, каждый раз пересчитывая значение функции в вершине. Изменить значение в листе очень просто (вспомним, что индексы листьев от nMax до 2*nMax-1). Значение i-го листа имеет индекс nMax+i :
a[nMax+i]= newValue;
Как известно, глубина полного бинарного дерева из m вершин равна log2m, поэтому мы должны выполнить данную операцию за логарифмическое время. Например, изменим a2 на a2I :
Что бы «обновить» ДО нам нужно записать в лист новое значение, а затем подняться до корня, каждый раз пересчитывая значение функции в вершине. Изменить значение в листе очень просто (вспомним, что индексы листьев от nMax до 2*nMax-1). Значение i-го листа имеет индекс nMax+i :
a[nMax+i]= newValue;
Слайд 6
Теперь осталось подняться до корня, это можно сделать с помощью цикла:
while
Теперь осталось подняться до корня, это можно сделать с помощью цикла:
while
(i>1)
{
i/= 2;
a[i]= f(a[2*i],a[2*i+1]);
}
{
i/= 2;
a[i]= f(a[2*i],a[2*i+1]);
}
Слайд 7
Найти значение функции на отрезке от l до r.
Наконец-то, мы добрались
Найти значение функции на отрезке от l до r.
Наконец-то, мы добрались
до самого интересного запроса. Стоит отметить, что частный случай, когда l=r разобран в пункте 2 и выполняется за константу, в общем же случае асимптотика логарифмическая.
Введем определения.
Фундаментальный отрезок – такой отрезок, для которого существует вершина в дереве, хранящая значение функции на данном отрезке.
Уровень.
Уровень корня – 1, а для каждого сына уровень на единицу больше, чем у родителя.
Введем определения.
Фундаментальный отрезок – такой отрезок, для которого существует вершина в дереве, хранящая значение функции на данном отрезке.
Уровень.
Уровень корня – 1, а для каждого сына уровень на единицу больше, чем у родителя.
Слайд 8
Для того, что бы вычислить значение функции на отрезке, нам необходимо
Для того, что бы вычислить значение функции на отрезке, нам необходимо
разбить его на МИНИМАЛЬНОЕ количество фундаментальных отрезков. Что бы найти значение для любой вершины (кроме листа), нам нужно знать значения для сыновей.
Мы будем спускаться по ДО. Изначально встаем в корень. Пусть мы находимся в какой-то вершине. Рассмотрим 3 возможных случая: отрезок [l..r] совпадает с отрезком, соответствующим текущей вершине, отрезок [l..r] полностью принадлежит одному из сыновей, отрезок принадлежит обоим сыновьям. В первом случае просто возвращаем посчитанное значение из ДО, во-втором – спускаемся в данного сына, в-третьем же случае разобьем данный отрезок на два: [l..правый конец левого сына] и [левый конец правого сына..r].
Рекурсивно вычислим значения для каждого из них.
Мы будем спускаться по ДО. Изначально встаем в корень. Пусть мы находимся в какой-то вершине. Рассмотрим 3 возможных случая: отрезок [l..r] совпадает с отрезком, соответствующим текущей вершине, отрезок [l..r] полностью принадлежит одному из сыновей, отрезок принадлежит обоим сыновьям. В первом случае просто возвращаем посчитанное значение из ДО, во-втором – спускаемся в данного сына, в-третьем же случае разобьем данный отрезок на два: [l..правый конец левого сына] и [левый конец правого сына..r].
Рекурсивно вычислим значения для каждого из них.
Слайд 9
Создаем вспомогательную функцию.
int query(int l, int r, int leftPosition, int rightPosition,
Создаем вспомогательную функцию.
int query(int l, int r, int leftPosition, int rightPosition,
int v)
{
// return value function f on the intersection segments [l;r] and [leftPosition;rightPosition]
// l – левая граница запроса
// r – правая граница запроса
// v – текущая вершина дерева отрезков
// [leftPosition; rightPosition] – отрезок соответствующий v
if (rif (l==leftPosition && r==rightPosition) return a[v];
// если отрезок фундаментальный,то возвращаем значение из вершины
// раз мы дошли сюда, то отрезок принадлежит сыновьям
int middle= (leftPosition+rightPosition)/2;
// вычисляем правую границу левого сына
return f(query(l,min(middle,r),leftPosition,middle,v*2),query(max(l,middle+1),r,middle+1,rightPosition,v*2+1));
// рекурсивно вычисляем запросы для сыновей
}
{
// return value function f on the intersection segments [l;r] and [leftPosition;rightPosition]
// l – левая граница запроса
// r – правая граница запроса
// v – текущая вершина дерева отрезков
// [leftPosition; rightPosition] – отрезок соответствующий v
if (r
// если отрезок фундаментальный,то возвращаем значение из вершины
// раз мы дошли сюда, то отрезок принадлежит сыновьям
int middle= (leftPosition+rightPosition)/2;
// вычисляем правую границу левого сына
return f(query(l,min(middle,r),leftPosition,middle,v*2),query(max(l,middle+1),r,middle+1,rightPosition,v*2+1));
// рекурсивно вычисляем запросы для сыновей
}
Слайд 10
const int N = 1e5; // limit for array size
int
const int N = 1e5; // limit for array size
int
n; // array size
int t[2 * N];
void build() {
// build the tree
for (int i = n - 1; i > 0; --i) t[i] = t[i*2] + t[i*2-1]; }
void modify(int p, int value) {
// set value at position p
for (t[p += n] = value; p > 1; p /=2 ) t[p/2] = t[p] + t[p^1];
}
int query(int l, int r)
{ // sum on interval [l, r)
int res = 0;
for (l += n, r += n; l < r; l /=2, r /= 2)
{
if (l%2==1) res += t[l++];
if (r%2==1) res += t[--r];
}
return res;
}
int t[2 * N];
void build() {
// build the tree
for (int i = n - 1; i > 0; --i) t[i] = t[i*2] + t[i*2-1]; }
void modify(int p, int value) {
// set value at position p
for (t[p += n] = value; p > 1; p /=2 ) t[p/2] = t[p] + t[p^1];
}
int query(int l, int r)
{ // sum on interval [l, r)
int res = 0;
for (l += n, r += n; l < r; l /=2, r /= 2)
{
if (l%2==1) res += t[l++];
if (r%2==1) res += t[--r];
}
return res;
}








 Блокчейн: потенциал роста
Блокчейн: потенциал роста Конспекты уроков 10 класс (1 четверть)
Конспекты уроков 10 класс (1 четверть) Организационное и правовое обеспечение информационной безопасности
Организационное и правовое обеспечение информационной безопасности Потоки и файлы. Часть 2 Работа с файлами
Потоки и файлы. Часть 2 Работа с файлами Тестирование с точки зрения тестировщика
Тестирование с точки зрения тестировщика Презентация Характеристика объекта
Презентация Характеристика объекта Регистрация в АИС Молодежь России
Регистрация в АИС Молодежь России Разработка алгоритмов сложной структуры для исполнителя. Стрелочка
Разработка алгоритмов сложной структуры для исполнителя. Стрелочка Технология создания видеоролика в редакторе SonyVegas
Технология создания видеоролика в редакторе SonyVegas Текстовые документы и технологии их создания. Документ. Текстовый документ. Структурные элементы текстового документа
Текстовые документы и технологии их создания. Документ. Текстовый документ. Структурные элементы текстового документа Элективный курс как средство профильного обучения на старшей ступени полного (среднего) образования
Элективный курс как средство профильного обучения на старшей ступени полного (среднего) образования Алфавитный подход к определению количества информации
Алфавитный подход к определению количества информации Структуризация логистических информационных систем веб-сайтов
Структуризация логистических информационных систем веб-сайтов Мой первый Startup. Онлайн платформа LARP Forge
Мой первый Startup. Онлайн платформа LARP Forge Модем. Арнайы құрылғы
Модем. Арнайы құрылғы Географические и земельные информационные системы
Географические и земельные информационные системы Введение в язык программирования С++
Введение в язык программирования С++ TechDays
TechDays Текст для сайта. Сервис Shato
Текст для сайта. Сервис Shato Электронные таблицы и правила их заполнения (1)
Электронные таблицы и правила их заполнения (1) Теоретические основы разработки базы данных технического состояния зданий и сооружений
Теоретические основы разработки базы данных технического состояния зданий и сооружений Устройство компьютера
Устройство компьютера VR/AR технологии в играх
VR/AR технологии в играх Научная статья: от идеи – до цитирований
Научная статья: от идеи – до цитирований Web Attacks: cross-site request forgery, SQL injection, cross-site scripting
Web Attacks: cross-site request forgery, SQL injection, cross-site scripting Компьютерные телекоммуникации
Компьютерные телекоммуникации Kutubxona faoliyatida elektron ta’lim kontentlarini yaratish
Kutubxona faoliyatida elektron ta’lim kontentlarini yaratish Описание программы. Меню школьной столовой
Описание программы. Меню школьной столовой