Содержание
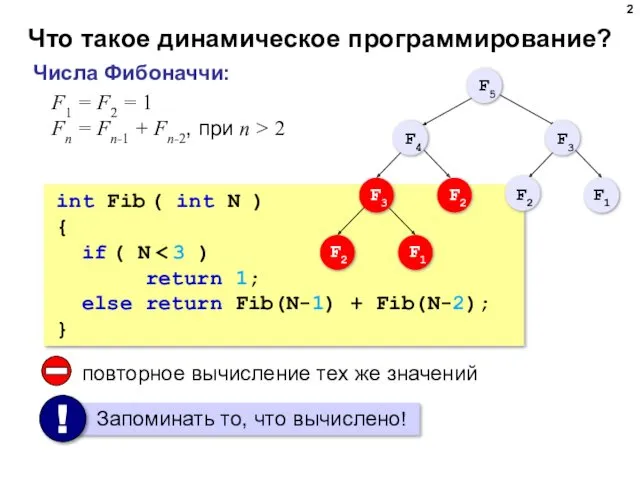
- 2. Что такое динамическое программирование? Числа Фибоначчи: ; . F1 = F2 = 1 Fn = Fn-1
- 3. Динамическое программирование Объявление массива: const int N = 10; int F[N+1]; // чтобы начать с 1
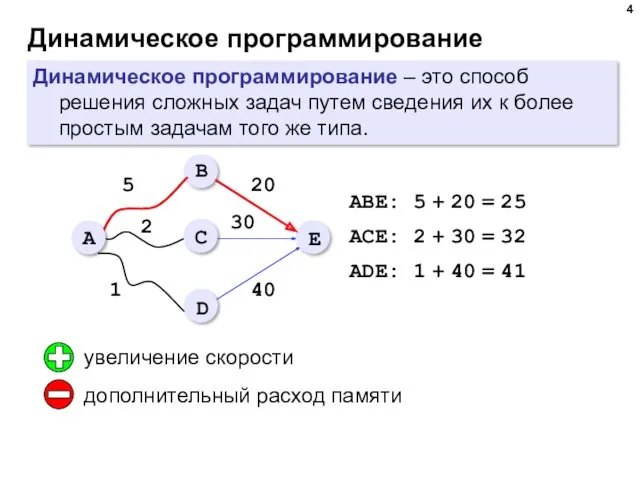
- 4. Динамическое программирование Динамическое программирование – это способ решения сложных задач путем сведения их к более простым
- 5. Количество вариантов Задача. Найти количество KN цепочек, состоящих из N нулей и единиц, в которых нет
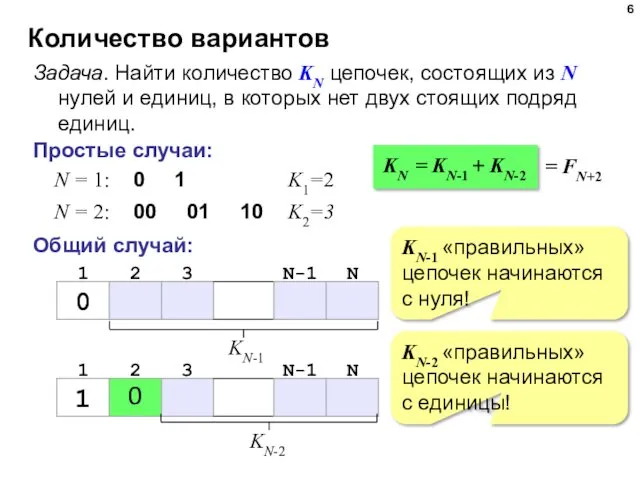
- 6. Количество вариантов Задача. Найти количество KN цепочек, состоящих из N нулей и единиц, в которых нет
- 7. Оптимальное решение Задача. В цистерне N литров молока. Есть бидоны объемом 1, 5 и 6 литров.
- 8. Жадный алгоритм – это многошаговый алгоритм, в котором на каждом шаге принимается решение, лучшее в данный
- 9. Оптимальное решение Сначала выбрали бидон… KN – минимальное число бидонов для N литров KN = 1
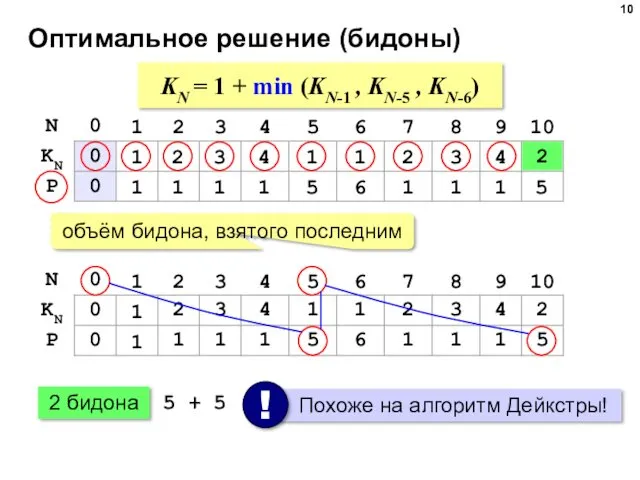
- 10. Оптимальное решение (бидоны) 1 1 2 1 3 1 4 1 1 5 1 6 2
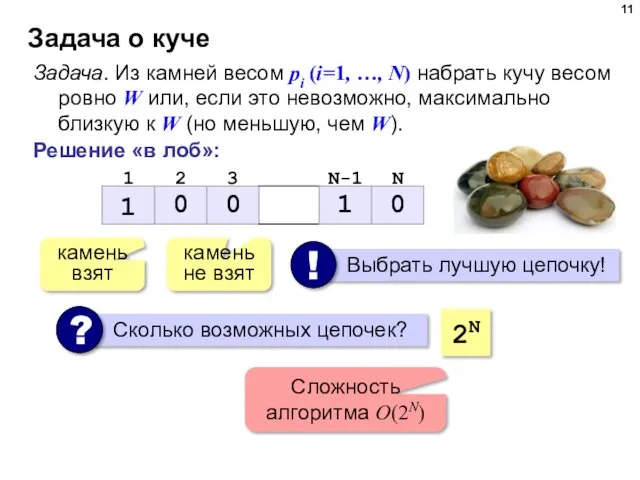
- 11. Задача о куче Задача. Из камней весом pi (i=1, …, N) набрать кучу весом ровно W
- 12. Задача о куче Задача. Из камней весом pi (i=1, …, N) набрать кучу весом ровно W
- 13. Задача о куче Добавляем камень с весом 4: для w 0 2 2 для w ≥
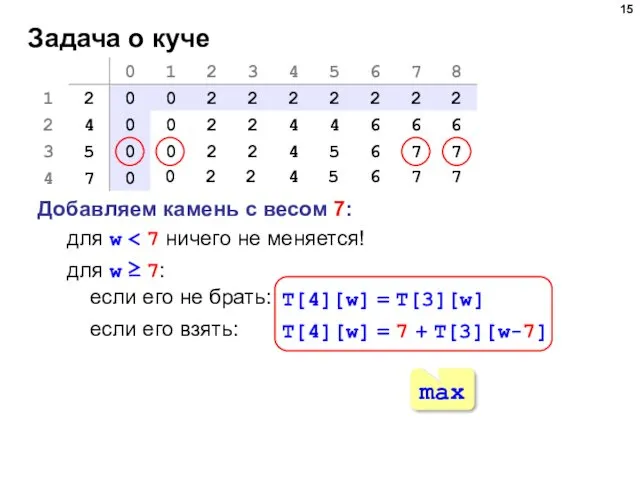
- 14. Задача о куче Добавляем камень с весом 5: для w 0 2 2 4 5 6
- 15. Задача о куче Добавляем камень с весом 7: для w 0 2 2 4 5 6
- 16. Задача о куче Добавляем камень с весом pi: для w Рекуррентная формула:
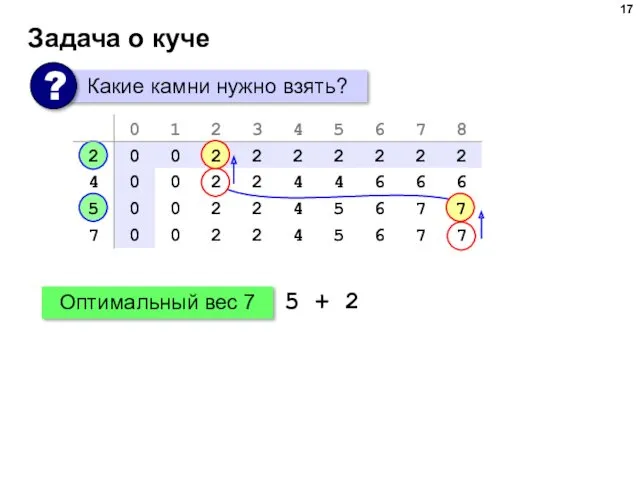
- 17. Задача о куче Оптимальный вес 7 5 + 2
- 18. Задача о куче Заполнение таблицы: W+1 N псевдополиномиальный
- 19. Количество программ Задача. У исполнителя Утроитель есть команды: 1. прибавь 1 2. умножь на 3 Сколько
- 20. Количество программ Как получить число N: N если делится на 3! последняя команда Рекуррентная формула: KN
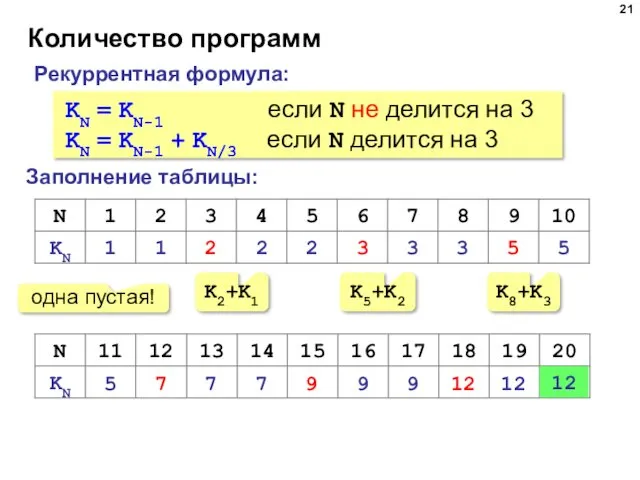
- 21. Количество программ Заполнение таблицы: Рекуррентная формула: KN = KN-1 если N не делится на 3 KN
- 22. Количество программ Только точки изменения: 12 20 Программа: K[1] = 1; for ( i = 2;
- 23. Размен монет Задача. Сколькими различными способами можно выдать сдачу размером W рублей, если есть монеты достоинством
- 24. Размен монет Пример: W = 10, монеты 1, 2, 5 и 10 w pi базовые случаи
- 25. Размен монет Пример: W = 10, монеты 1, 2, 5 и 10 Рекуррентная формула (добавили монету
- 27. Скачать презентацию












![Количество программ Только точки изменения: 12 20 Программа: K[1] =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/89211/slide-21.jpg)



 Database and management. Lecture 1
Database and management. Lecture 1 Компьютерная графика. Лекция 7
Компьютерная графика. Лекция 7 Информационные технологии. Введение. Отрасль информационных технологий
Информационные технологии. Введение. Отрасль информационных технологий Рекламная сеть Яндекса
Рекламная сеть Яндекса Database systems
Database systems Здоровьесберегающие технологии в предметной деятельности Информатика и ИКТ
Здоровьесберегающие технологии в предметной деятельности Информатика и ИКТ Знакомство с операционной системой MAC OS
Знакомство с операционной системой MAC OS ЗАСОБИ СТВОРЕННЯ ЕЛЕКТРОННОГО ДОКУМЕНТООБІГУ
ЗАСОБИ СТВОРЕННЯ ЕЛЕКТРОННОГО ДОКУМЕНТООБІГУ Компьютерные презентации. Мультимедиа. Информатика. 7 класс
Компьютерные презентации. Мультимедиа. Информатика. 7 класс Языки программирования. Язык Паскаль
Языки программирования. Язык Паскаль Законы алгебры логики. Равносильные преобразования
Законы алгебры логики. Равносильные преобразования Сетевые интерфейсы
Сетевые интерфейсы Введение в язык программирования С++
Введение в язык программирования С++ Система информационной безопасности локально-вычислительной сети
Система информационной безопасности локально-вычислительной сети Порівняльна характеристика 5 офіційних сайтів **** готелів Львова
Порівняльна характеристика 5 офіційних сайтів **** готелів Львова 2D Pipe Junction. Introduction to ANSYS ICEM CFD
2D Pipe Junction. Introduction to ANSYS ICEM CFD Градиентный бустинг
Градиентный бустинг Разработка проекта локальной сети предприятия с использованием программного эмулятора оборудования Cisco Packet Tracer
Разработка проекта локальной сети предприятия с использованием программного эмулятора оборудования Cisco Packet Tracer Инфо-умники и умницы. Викторина
Инфо-умники и умницы. Викторина Аватар, ЦА, золотые вопросы
Аватар, ЦА, золотые вопросы Изобретения, изменившие мир
Изобретения, изменившие мир Понятие информации. Виды и свойства информации
Понятие информации. Виды и свойства информации Анализ и синтез систем
Анализ и синтез систем Висловлювання. Істинні та хибні висловлювання (урок 10, 7 клас)
Висловлювання. Істинні та хибні висловлювання (урок 10, 7 клас) Академическое письмо. Подготовка теоретической основы научного исследования
Академическое письмо. Подготовка теоретической основы научного исследования Аддитивные технологии
Аддитивные технологии Сортировщик деталей
Сортировщик деталей Компьютерные сети. Введение
Компьютерные сети. Введение