Содержание
- 4. Dynamic Programming Dynamic programming is a very powerful, general tool for solving optimization problems. Once understood
- 5. Greedy Algorithms Greedy algorithms focus on making the best local choice at each decision point. For
- 6. Problem: Let’s consider the calculation of Fibonacci numbers: F(n) = F(n-2) + F(n-1) with seed values
- 7. Recursive Algorithm: Fib(n) { if (n == 0) return 0; if (n == 1) return 1;
- 8. Recursive Algorithm: Fib(n) { if (n == 0) return 0; if (n == 1) return 1;
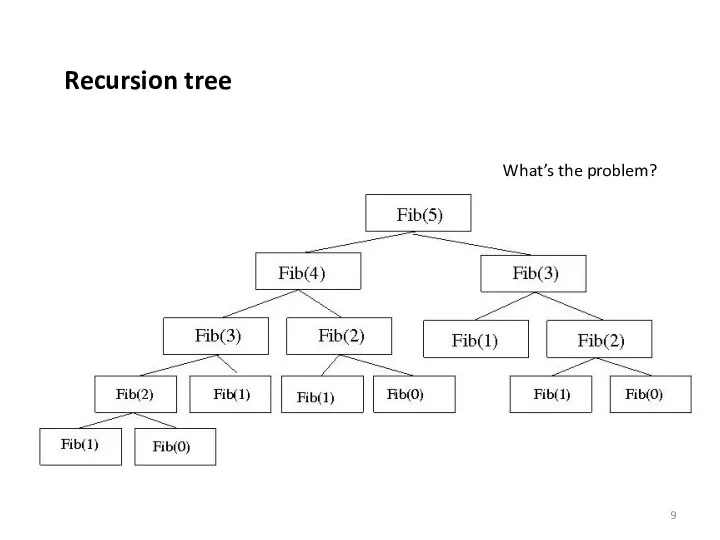
- 9. Recursion tree What’s the problem?
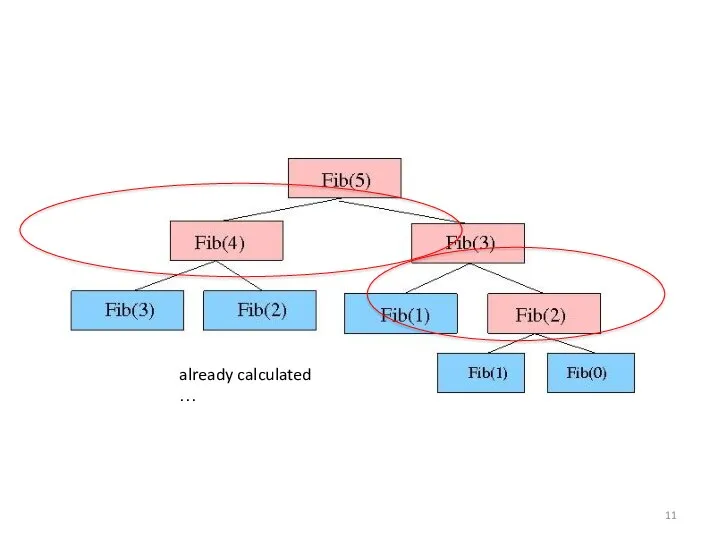
- 10. Memoization: Fib(n) { if (n == 0) return M[0]; if (n == 1) return M[1]; if
- 11. already calculated …
- 12. Dynamic programming - Main approach: recursive, holds answers to a sub problem in a table, can
- 13. 1-dimensional DP Problem
- 14. 1-dimensional DP Problem
- 15. 1-dimensional DP Problem
- 16. 1-dimensional DP Problem
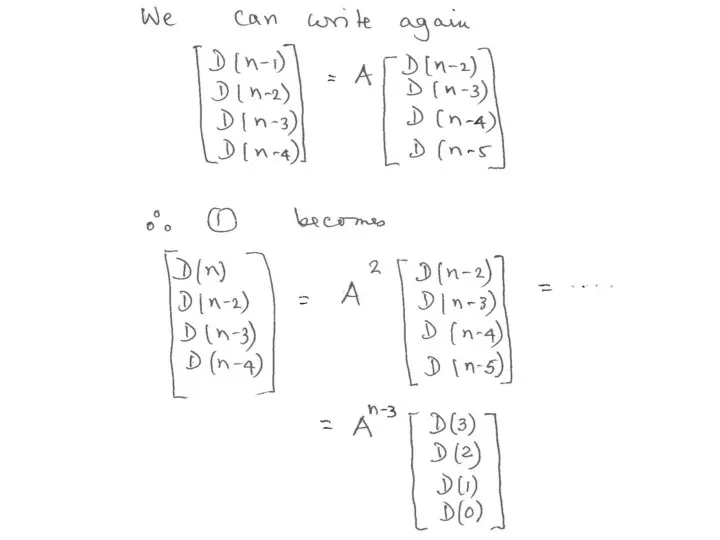
- 17. What happens when n is extremely large?
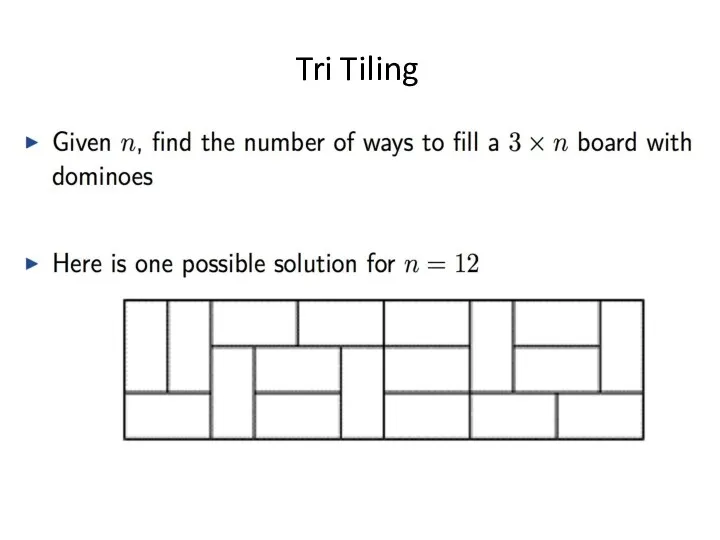
- 21. Tri Tiling
- 22. Tri Tiling
- 23. Tri Tiling
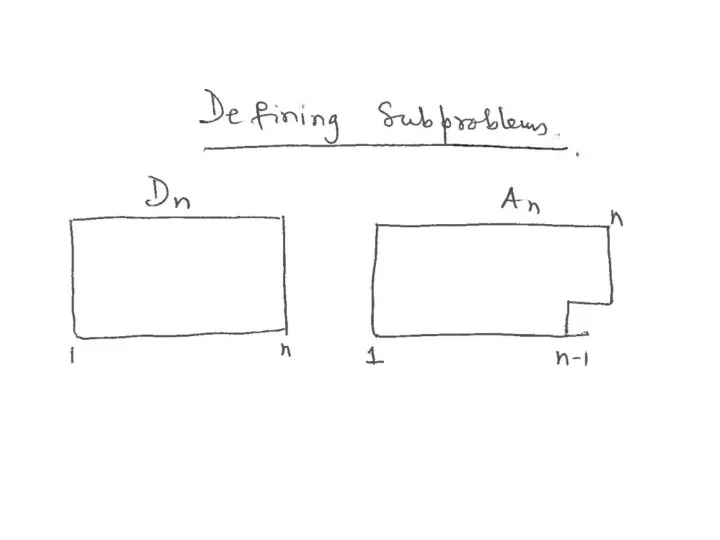
- 25. Finding Recurrences
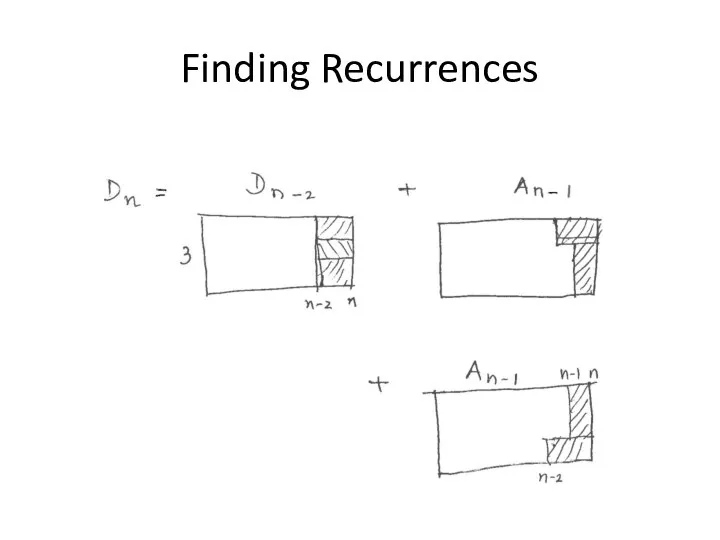
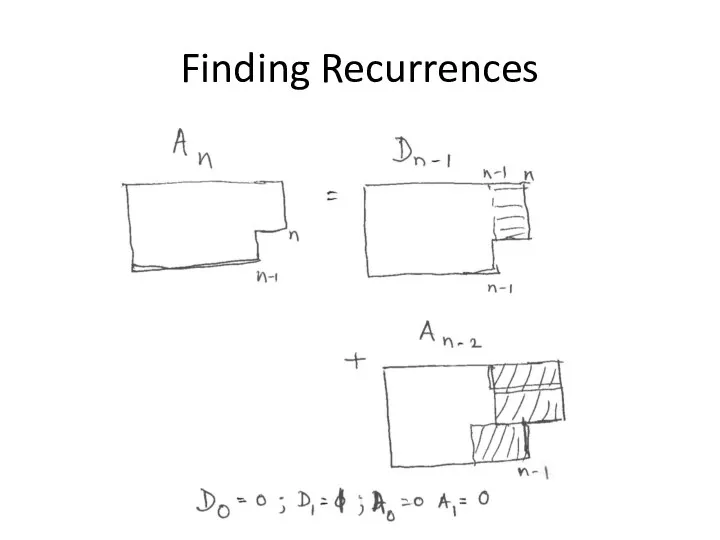
- 26. Finding Recurrences
- 27. Extension Solving the problem for n x m grids, where n is small, say n ≤
- 29. Egg dropping problem
- 30. Egg dropping problem
- 31. Egg dropping problem
- 32. Egg dropping problem
- 33. Egg dropping problem
- 34. Egg dropping problem
- 35. Egg dropping problem
- 36. Egg dropping problem(n eggs) Dynamic Programming Approach D[j,m] : There are j floors and m eggs.
- 37. Egg dropping problem(n eggs) Dynamic Programming Approach DP[j,m] : There are j floors and m eggs.
- 38. Egg dropping problem(n eggs) Dynamic Programming Approach DP[j,m] : There are j floors and m eggs.
- 48. Coin-change Problem To find the minimum number of Canadian coins to make any amount, the greedy
- 49. Coin-change Problem The greedy method doesn’t work if we didn’t have 5¢ coin. For 31¢, the
- 50. Coin set for examples For the following examples, we will assume coins in the following denominations:
- 51. A solution We can reduce the problem recursively by choosing the first coin, and solving for
- 52. A dynamic programming solution Idea: Solve first for one cent, then two cents, then three cents,
- 53. A dynamic programming solution Let T(n) be the number of coins taken to dispense n¢. The
- 54. A dynamic programming solution The dynamic programming algorithm is O(N*K) where N is the desired amount
- 55. Comparison with divide-and-conquer Divide-and-conquer algorithms split a problem into separate subproblems, solve the subproblems, and combine
- 56. Comparison with divide-and-conquer In contrast, a dynamic programming algorithm proceeds by solving small problems, remembering the
- 57. The principle of optimality, I Dynamic programming is a technique for finding an optimal solution The
- 58. The principle of optimality, I Example: Consider the problem of making N¢ with the fewest number
- 59. The principle of optimality, II The principle of optimality holds if Every optimal solution to a
- 60. The principle of optimality, II Example: In coin problem, The optimal solution to 7¢ is 5¢
- 61. Longest simple path Consider the following graph: The longest simple path (path not containing a cycle)
- 62. Example: In coin problem, The optimal solution to 7¢ is 5¢ + 1¢ + 1¢, and
- 63. The 0-1 knapsack problem A thief breaks into a house, carrying a knapsack... He can carry
- 64. The 0-1 knapsack problem A greedy algorithm does not find an optimal solution A dynamic programming
- 65. The 0-1 knapsack problem This is similar to, but not identical to, the coins problem In
- 66. Steps for Solving DP Problems Define subproblems Write down the recurrence that relates subproblems Recognize and
- 67. Comments Dynamic programming relies on working “from the bottom up” and saving the results of solving
- 69. Скачать презентацию







![Memoization: Fib(n) { if (n == 0) return M[0]; if](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/598664/slide-9.jpg)



















![Egg dropping problem(n eggs) Dynamic Programming Approach D[j,m] : There](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/598664/slide-35.jpg)
![Egg dropping problem(n eggs) Dynamic Programming Approach DP[j,m] : There](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/598664/slide-36.jpg)
![Egg dropping problem(n eggs) Dynamic Programming Approach DP[j,m] : There](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/598664/slide-37.jpg)





























 Текстовая информация
Текстовая информация использование игр на уроке информатики в начальной школе
использование игр на уроке информатики в начальной школе Spatial Data Structures
Spatial Data Structures Применение ИКТ на уроках музыки
Применение ИКТ на уроках музыки Людина у світі інформації
Людина у світі інформації Организация вычислений в электронных таблицах. Обработка числовой информации в электронных таблицах. Информатика. 9 класс
Организация вычислений в электронных таблицах. Обработка числовой информации в электронных таблицах. Информатика. 9 класс Презентация Решение олимпиадных задач. Игра Баше
Презентация Решение олимпиадных задач. Игра Баше Социальные сети для бизнеса
Социальные сети для бизнеса Testing Throughout the Software Life Cycle: Test Levels. Types of Software Testing (Topic 4)
Testing Throughout the Software Life Cycle: Test Levels. Types of Software Testing (Topic 4) Включение системы. Настройка и контроль системы перед отправлением
Включение системы. Настройка и контроль системы перед отправлением Онлайн-кассы
Онлайн-кассы Шаблоны параллельного проектирования
Шаблоны параллельного проектирования 9 класс Презентации к урокам
9 класс Презентации к урокам Управление данными
Управление данными Инновационный проект
Инновационный проект Основы логики.
Основы логики. Общие и отличительные свойства объектов
Общие и отличительные свойства объектов Основы теории коммуникации
Основы теории коммуникации Киберспорт - это спорт?
Киберспорт - это спорт? HTML программалау тілі
HTML программалау тілі Графический редактор Paint
Графический редактор Paint Объекты JavaScript
Объекты JavaScript Ақпараттық қауіпсіздікті қамтамасыз ету комплексті тәсілі. Ақпараттық қауіпсіздік негізгі ұғымдары
Ақпараттық қауіпсіздікті қамтамасыз ету комплексті тәсілі. Ақпараттық қауіпсіздік негізгі ұғымдары Формализация понятия алгоритма
Формализация понятия алгоритма Культура использования информации. Библиографическое оформление результатов поиска информации
Культура использования информации. Библиографическое оформление результатов поиска информации Solid - принципы с примерами PHP
Solid - принципы с примерами PHP Организация интернет-СМИ
Организация интернет-СМИ Разработка информационного обеспечения для поддержки деятельности предприятия сферы услуг
Разработка информационного обеспечения для поддержки деятельности предприятия сферы услуг