Содержание
- 2. Определение двоичного дерева поиска Двоичное дерево называется деревом поиска, если для каждого узла дерева выполняется условие:
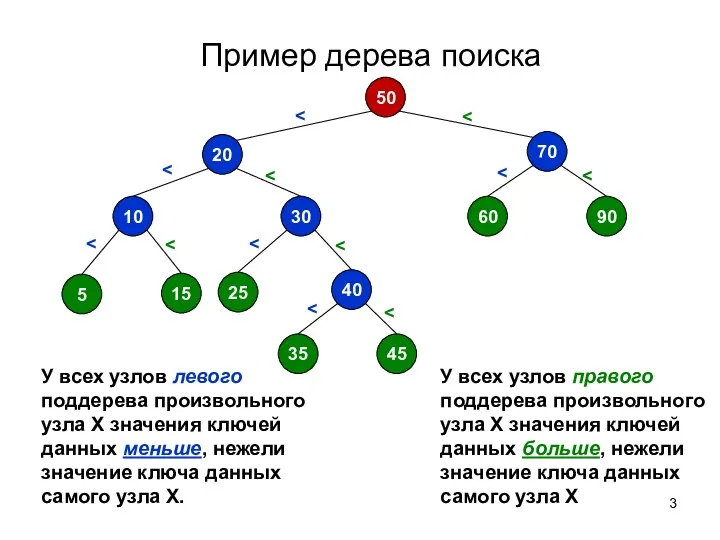
- 3. Пример дерева поиска У всех узлов правого поддерева произвольного узла X значения ключей данных больше, нежели
- 4. Операции над деревьями поиска Основные операции при работе с деревьями поиска не отличаются от обычного двоичного
- 5. Добавление узла в дерево поиска Если корень поддерева пуст, поместить в него заданный ключ; закончить алгоритм.
- 6. Добавление узла в дерево поиска //ToDo: сделать метод родителя виртуальным Node *addNode(Node *root, int key) override
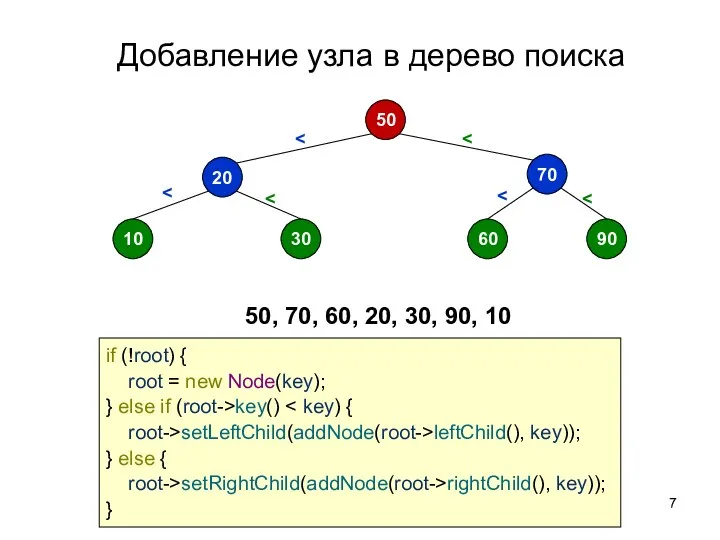
- 7. Добавление узла в дерево поиска if (!root) { root = new Node(key); } else if (root->key()
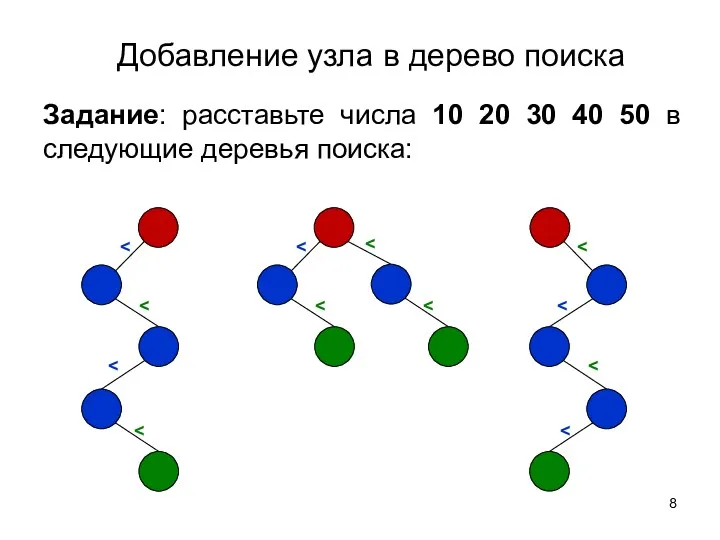
- 8. Добавление узла в дерево поиска Задание: расставьте числа 10 20 30 40 50 в следующие деревья
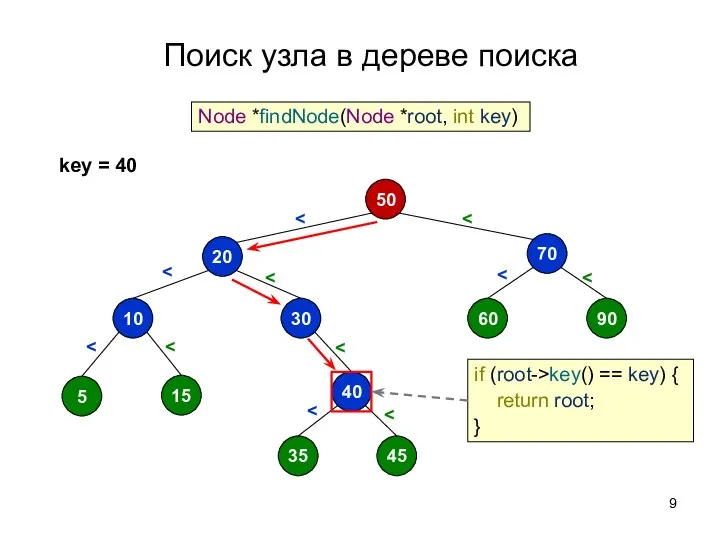
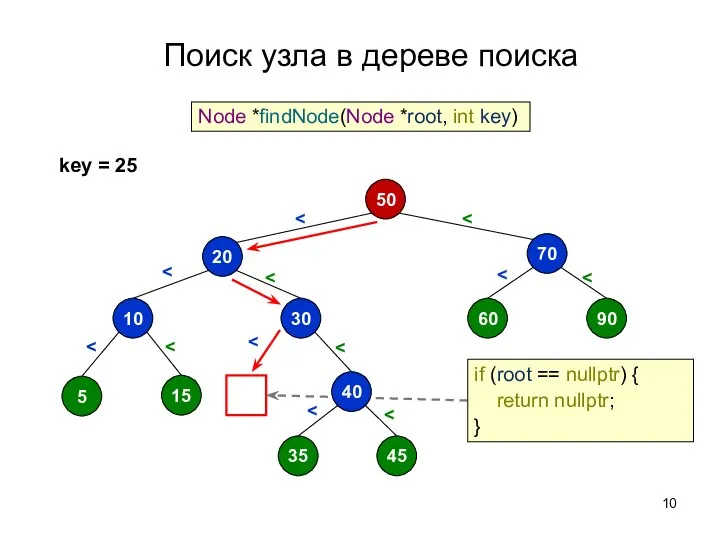
- 9. Поиск узла в дереве поиска 50 70 60 90 20 30 10 5 15 40 35
- 10. Поиск узла в дереве поиска 50 70 60 90 20 30 10 5 15 40 35
- 11. Удаление узла из дерева поиска Аналогично двоичному дереву, при удалении узла из дерева поиска возможны три
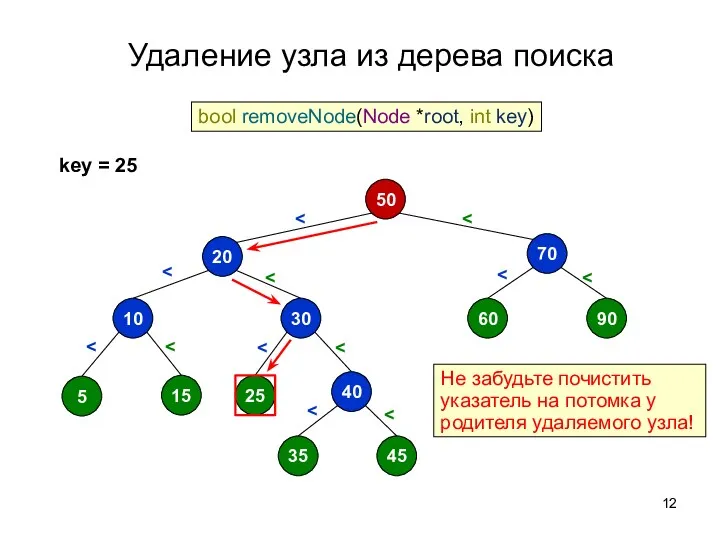
- 12. Удаление узла из дерева поиска 50 70 60 90 20 30 10 5 15 40 35
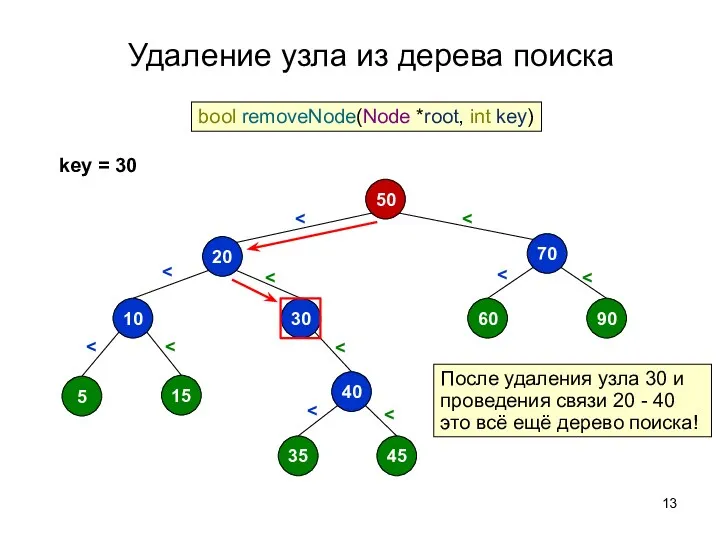
- 13. Удаление узла из дерева поиска 50 70 60 90 20 30 10 5 15 40 35
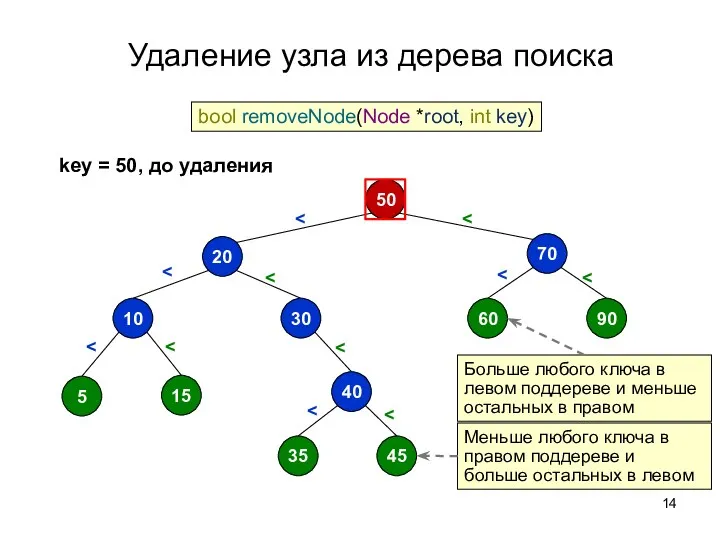
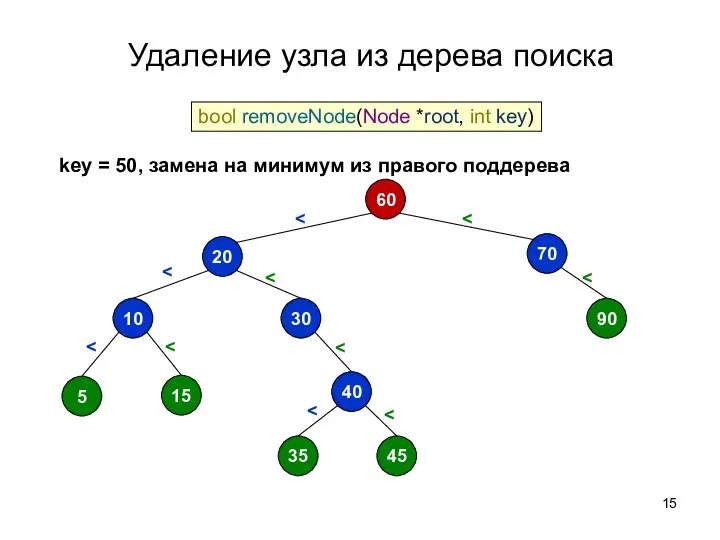
- 14. Удаление узла из дерева поиска 50 70 60 90 20 30 10 5 15 40 35
- 15. Удаление узла из дерева поиска 60 70 90 20 30 10 5 15 40 35 45
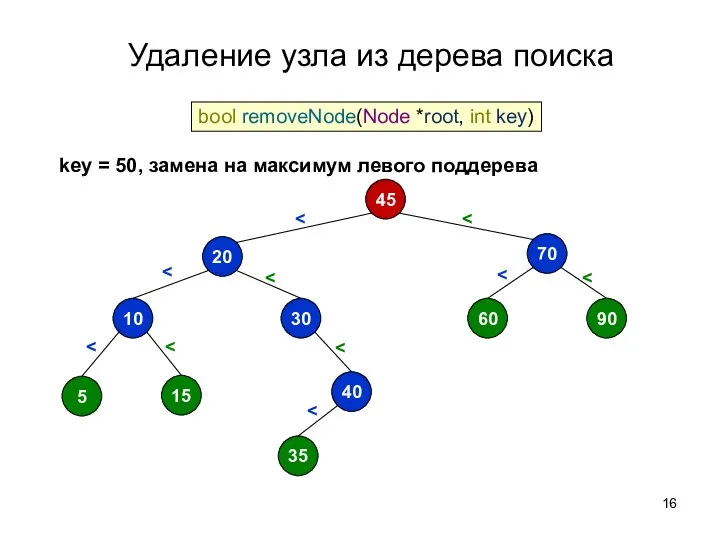
- 16. Удаление узла из дерева поиска 45 70 60 90 20 30 10 5 15 40 35
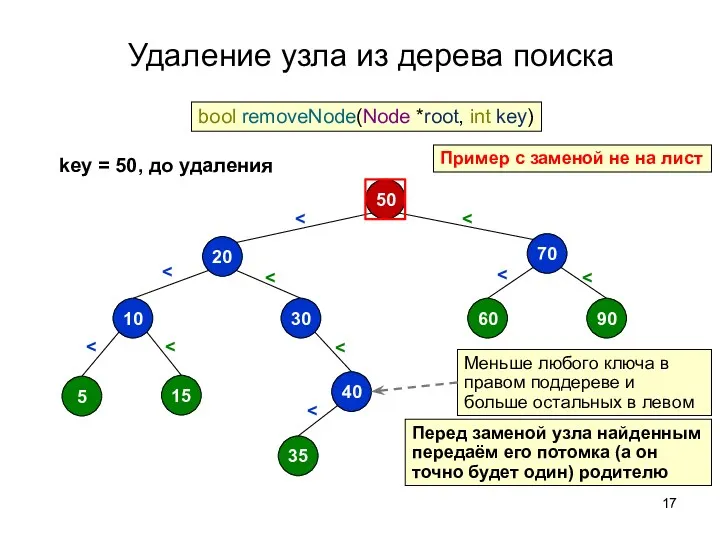
- 17. Удаление узла из дерева поиска 50 70 60 90 20 30 10 5 15 40 35
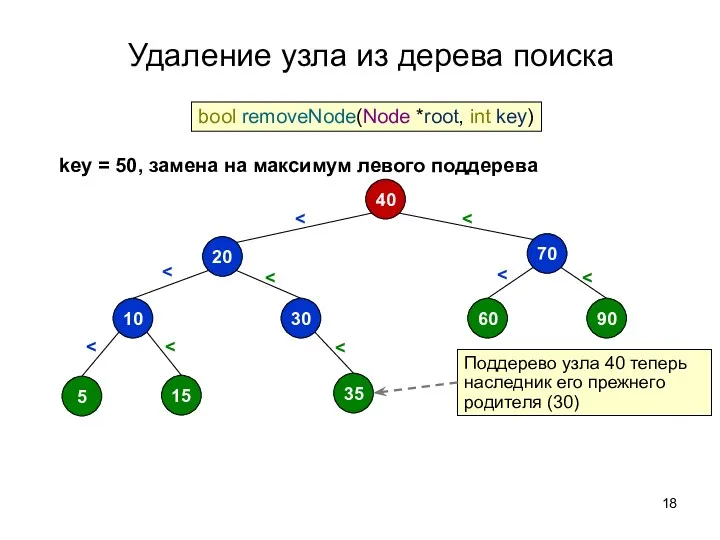
- 18. Удаление узла из дерева поиска 40 70 60 90 20 30 10 5 15 35 bool
- 19. Удаление узла из дерева поиска Алгоритм определения узла r, который заменит удаляемый узел n: Тривиальные случаи:
- 20. Удаление узла из дерева поиска Замечание: аналогично можно выполнить удаление ключа, спускаясь по левой ветви от
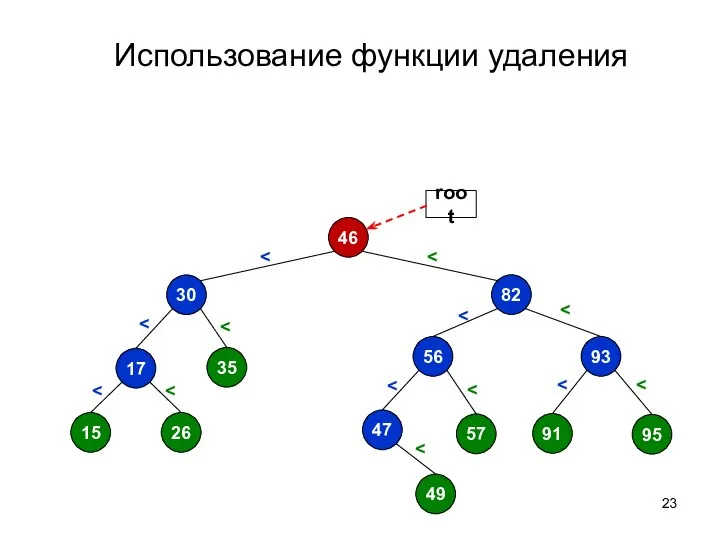
- 21. Использование функции удаления Пусть функция удаления узла имеет сигнатуру: Node *removeNode(Node *node) И удаляет переданный узел,
- 22. Использование функции удаления Node *removeEvenNodes(Node *root) { if (root == nullptr) { return nullptr; } root->setLeftChild(removeEvenNodes(root->leftChild()));
- 23. Использование функции удаления 46 35 82 56 93 95 91 47 49 30 17 26 15
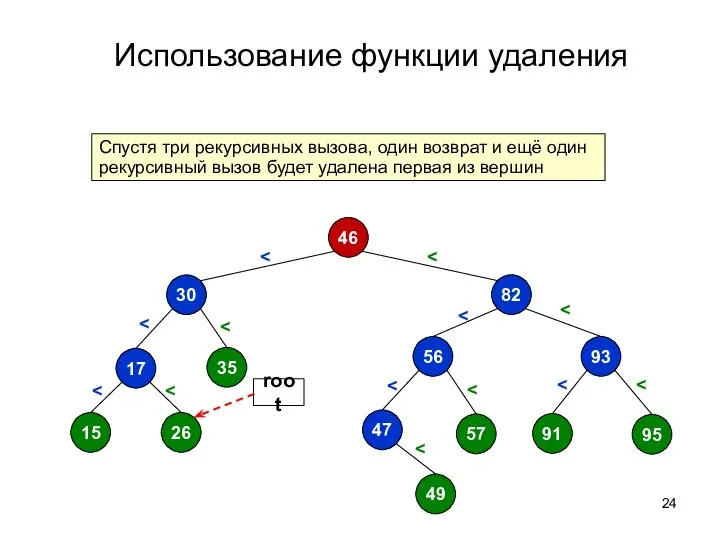
- 24. Использование функции удаления 46 35 82 56 93 95 91 47 49 30 17 26 15
- 25. Использование функции удаления 46 35 82 56 93 95 91 47 49 30 17 15 57
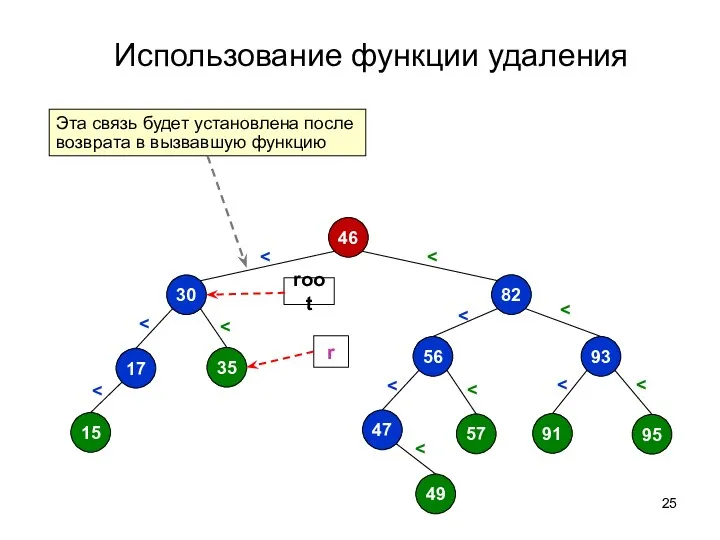
- 26. Использование функции удаления 46 82 56 93 95 91 47 49 35 17 15 57 root
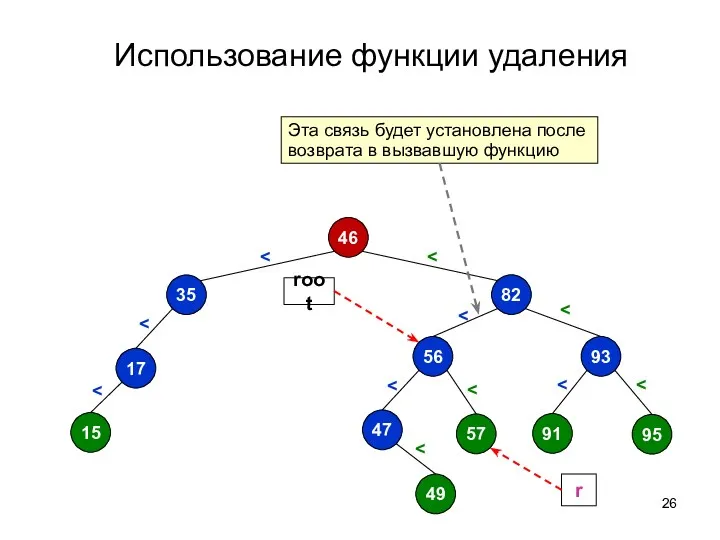
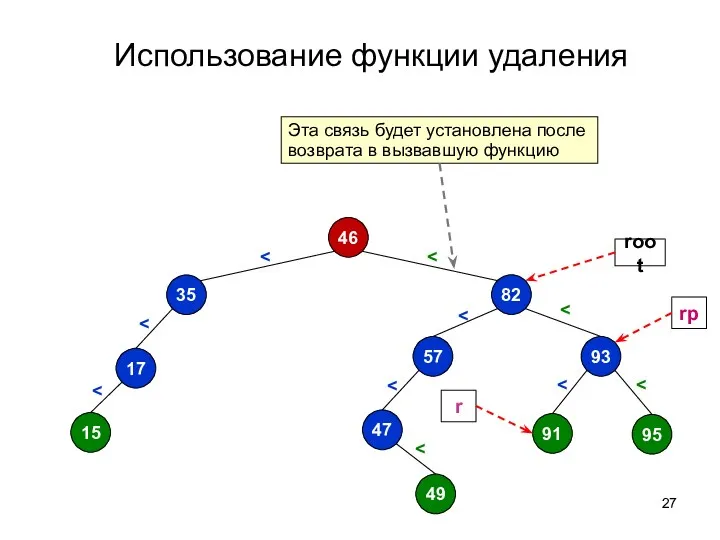
- 27. Использование функции удаления 46 82 57 93 95 91 47 49 35 17 15 rp root
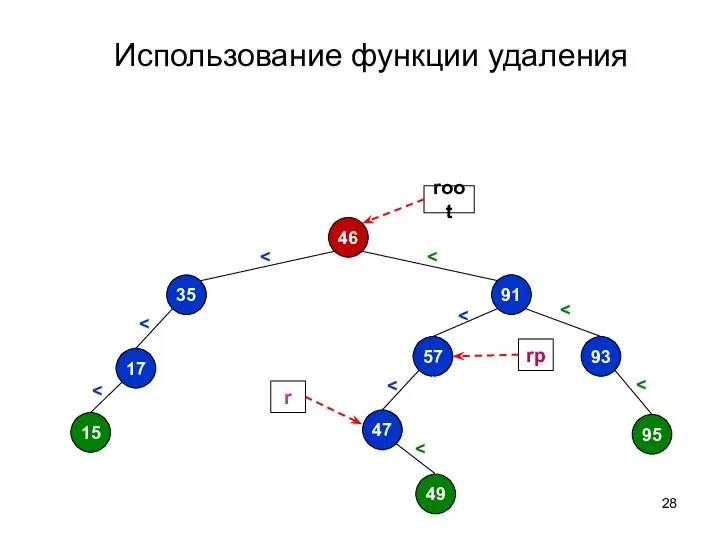
- 28. Использование функции удаления 46 91 57 93 95 47 49 35 17 15 rp root r
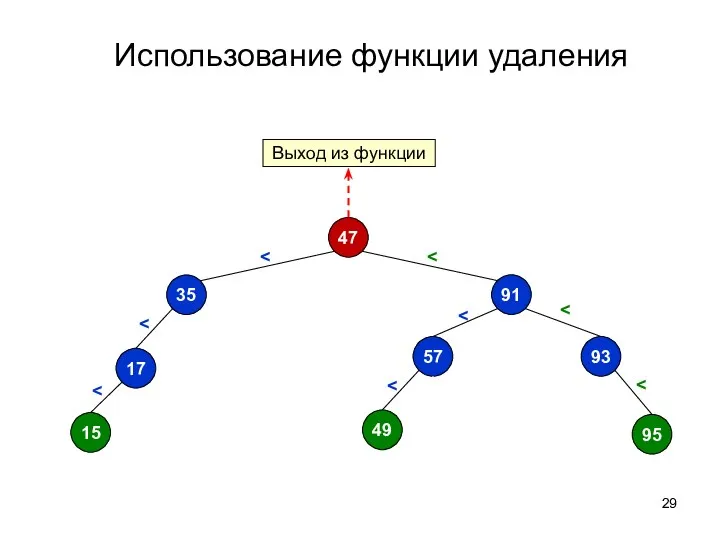
- 29. Использование функции удаления 47 91 57 93 95 49 35 17 15 Выход из функции
- 30. Обход дерева поиска Обход дерева поиска может выполняться по тем же правилам, что и обход любого
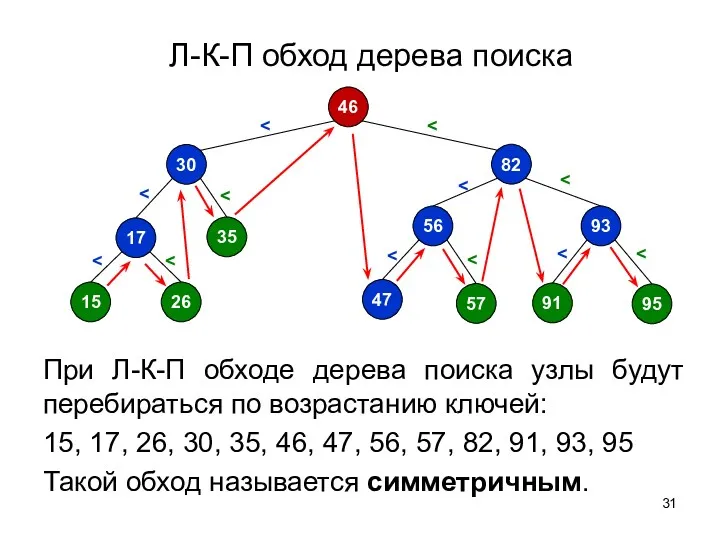
- 31. Л-К-П обход дерева поиска При Л-К-П обходе дерева поиска узлы будут перебираться по возрастанию ключей: 15,
- 32. Л-К-П обход дерева поиска //Пример реализации обхода //Вместо вывода в этот раз складываем ключи узлов в
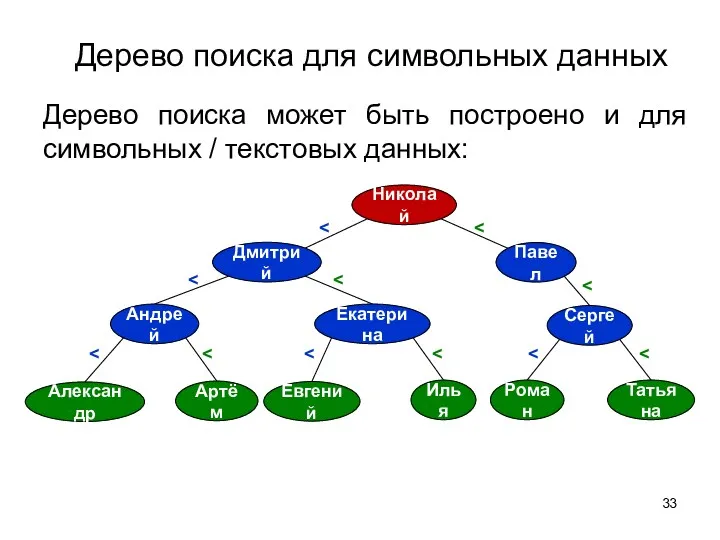
- 33. Дерево поиска для символьных данных Дерево поиска может быть построено и для символьных / текстовых данных:
- 35. Скачать презентацию











 Компьютерные вирусы. Типы, виды, пути заражения
Компьютерные вирусы. Типы, виды, пути заражения Основные правила безопасности интернета
Основные правила безопасности интернета Информатика пә ніне тақырыбында: модем
Информатика пә ніне тақырыбында: модем Триггеры в презентации. Применение. Создание слайдов с триггерами
Триггеры в презентации. Применение. Создание слайдов с триггерами Управление отношениями с клиентами. Исследование информационных технологий
Управление отношениями с клиентами. Исследование информационных технологий A binary Hopfield neural network
A binary Hopfield neural network Принципы организации VPN
Принципы организации VPN Cover title
Cover title Построение базы данных
Построение базы данных Списки. Односпрямований (однозв'язний) список. Друк (перегляд) однозв’язного списку
Списки. Односпрямований (однозв'язний) список. Друк (перегляд) однозв’язного списку Средства массовой информации (СМИ) и их роль в современном обществе
Средства массовой информации (СМИ) и их роль в современном обществе Апаратне забезпечення інформаційних систем. Історія розвитку обчислювальної техніки. (Урок 4)
Апаратне забезпечення інформаційних систем. Історія розвитку обчислювальної техніки. (Урок 4) Задача 20.1
Задача 20.1 Онлайн конференции, анкетирование, дистанционные курсы, интернет-олимпиады, компьютерное тестирование
Онлайн конференции, анкетирование, дистанционные курсы, интернет-олимпиады, компьютерное тестирование Программирование на языке ассемблер. Система команд процессора
Программирование на языке ассемблер. Система команд процессора Системы счисления. Методы перевода чисел из одной системы в другую
Системы счисления. Методы перевода чисел из одной системы в другую Маршрутизация. Вставка
Маршрутизация. Вставка Социальные сети
Социальные сети Android 6 Расширенная интерактивность
Android 6 Расширенная интерактивность Как работать в системе АИС Путевка
Как работать в системе АИС Путевка Государственая система научно-технической информации. (Лекция 2)
Государственая система научно-технической информации. (Лекция 2) Компания IT-Center
Компания IT-Center Инструкция по поиску информации в базе данных Springer
Инструкция по поиску информации в базе данных Springer Язык программирования Pascal
Язык программирования Pascal Сетевые атаки
Сетевые атаки Профилактика интернет-рисков и угроз жизни детей и подростков
Профилактика интернет-рисков и угроз жизни детей и подростков Бұлттық технологиялар
Бұлттық технологиялар Программирование на языке Python
Программирование на языке Python