Содержание
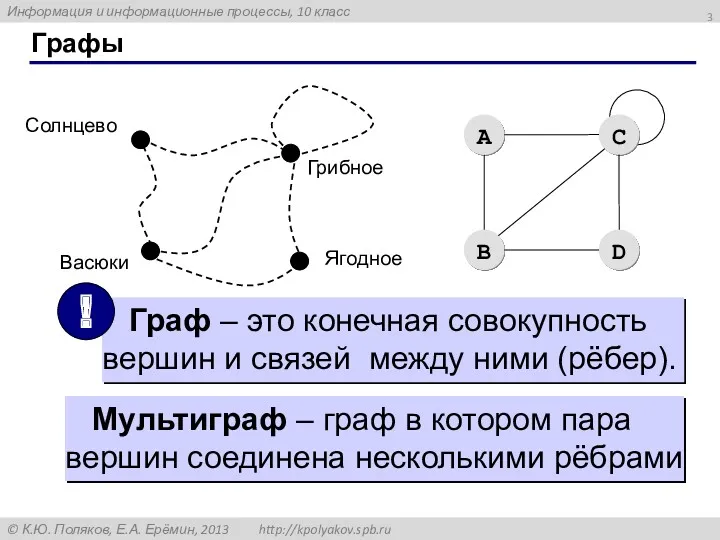
- 2. Графы «От посёлка Васюки три дороги идут в посёлки Солнцево, Грибное и Ягодное. Между Солнцевым и
- 3. Графы Мультиграф – граф в котором пара вершин соединена несколькими рёбрами
- 4. Граф (англ. graph) — совокупность непустого множества вершин и наборов пар вершин (связей между вершинами); основной
- 5. Граф, или неориентированный граф G— это упорядоченная пара G:=(V,E), где V — это непустое множество вершин
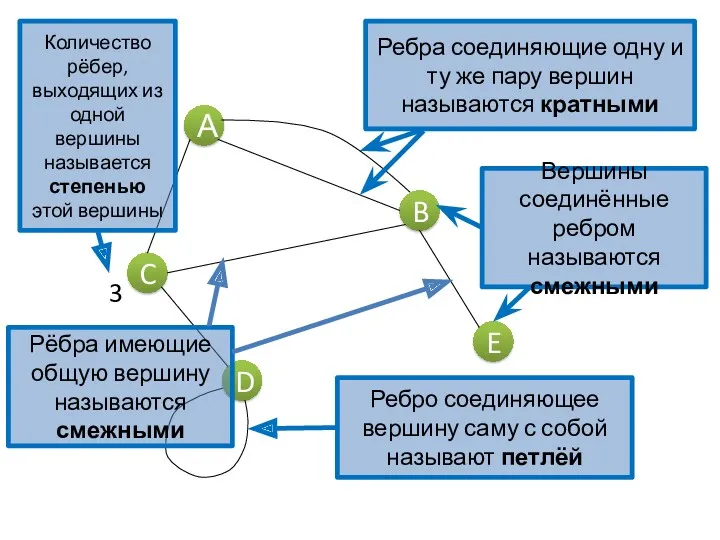
- 6. Вершины и рёбра графа называются также элементами графа, число вершин в графе |V| — порядком, число
- 7. Два ребра называются кратными, если множества их концевых вершин совпадают. Ребро называется петлёй, если его концы
- 8. А B D C E 3
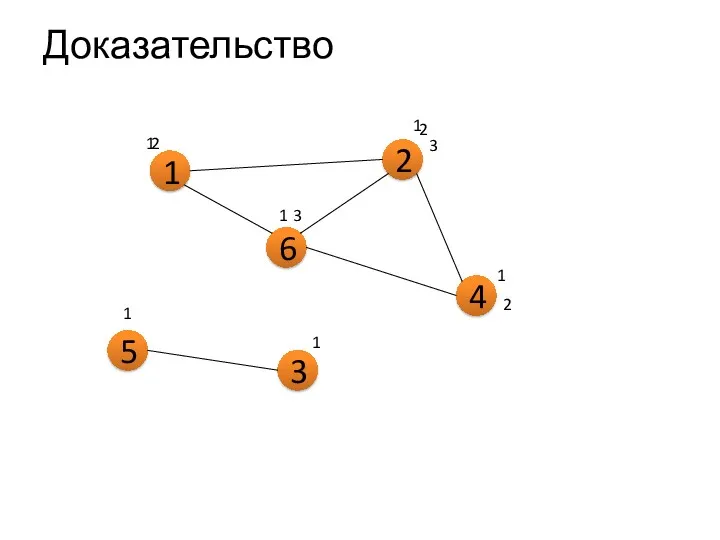
- 9. Теорема о сумме степеней вершин графа Сумма степеней всех вершин графа (или мультиграфа без петель) —
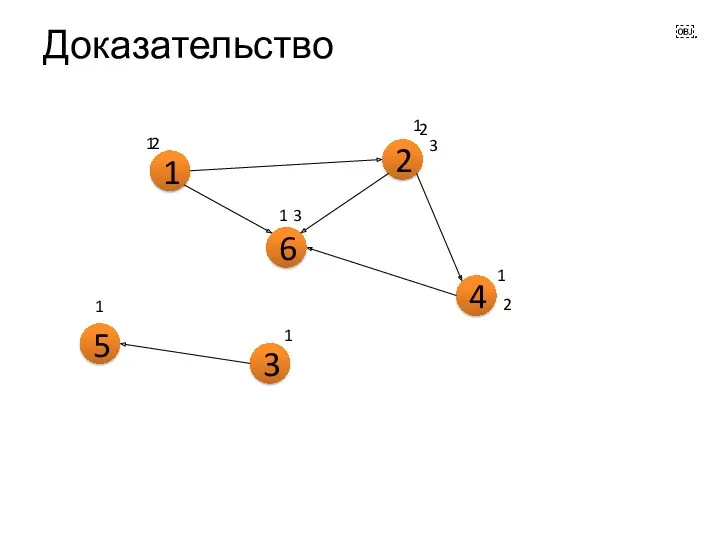
- 10. Доказательство 1 2 4 6 1 1 2 1 1 2 3 2 3
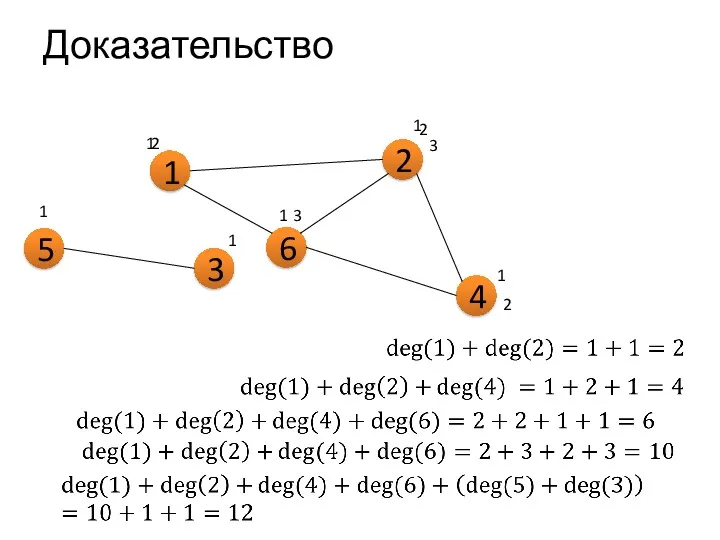
- 11. Доказательство 1 2 4 6 1 1 2 1 1 2 3 2 3
- 12. для ориентированного графа:
- 13. Доказательство 1 2 4 6 1 1 2 1 1 2 3 2 3 3 5
- 14. Лемма о рукопожатиях В любом графе число вершин нечётной степени чётно. В любой момент времени количество
- 15. Теорема о существовании вершин одинаковой степени В любом графе есть по крайней мере две вершины, имеющие
- 16. Теорема о существовании вершин одинаковой степени
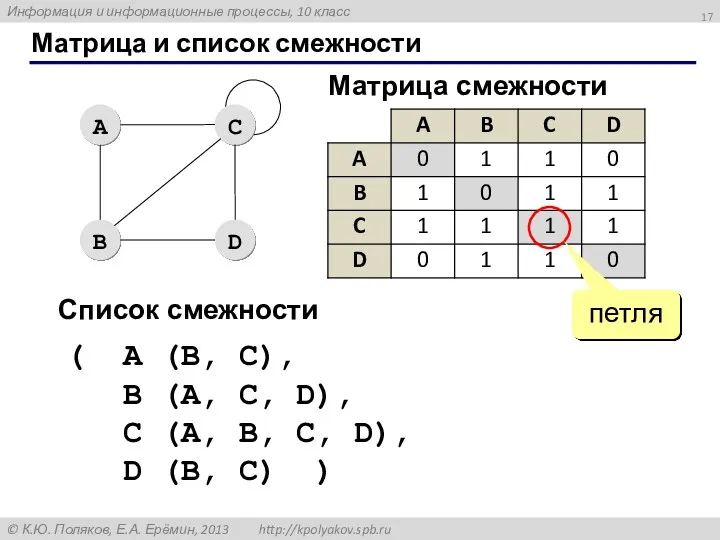
- 17. Матрица и список смежности петля Матрица смежности Список смежности ( A (B, C), B (A, C,
- 18. Способы представления графа в информатике Матрица смежности - бинарная матрица каждой ячейке которой записывается число, определяющее
- 19. Способы представления графа в информатике Список смежности —каждой вершине графа соответствует список, состоящий из "соседей" этой
- 20. Маршрутом в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей
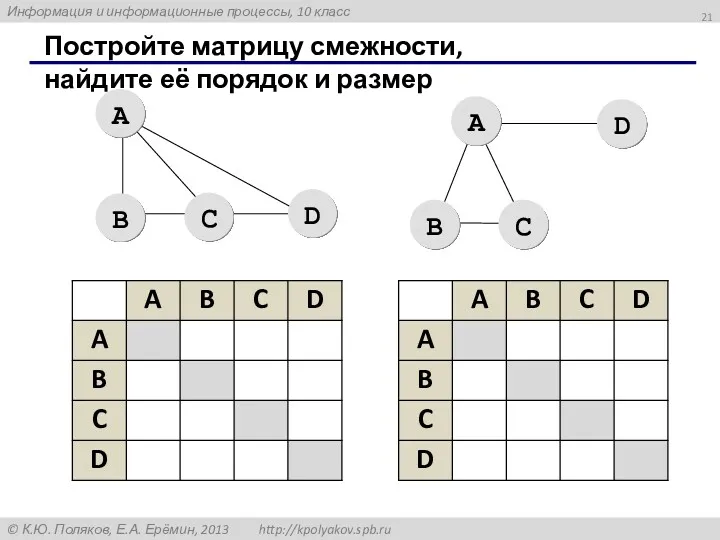
- 21. Постройте матрицу смежности, найдите её порядок и размер
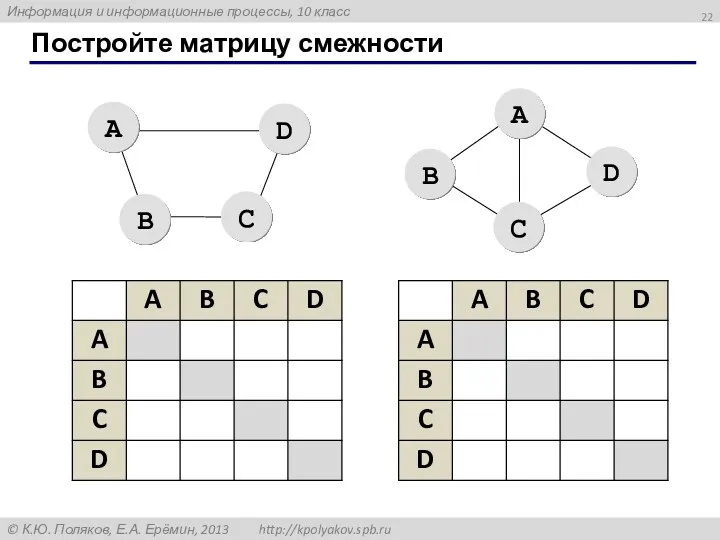
- 22. Постройте матрицу смежности
- 23. Нарисуйте граф
- 24. Нарисуйте граф
- 25. Нарисуйте граф
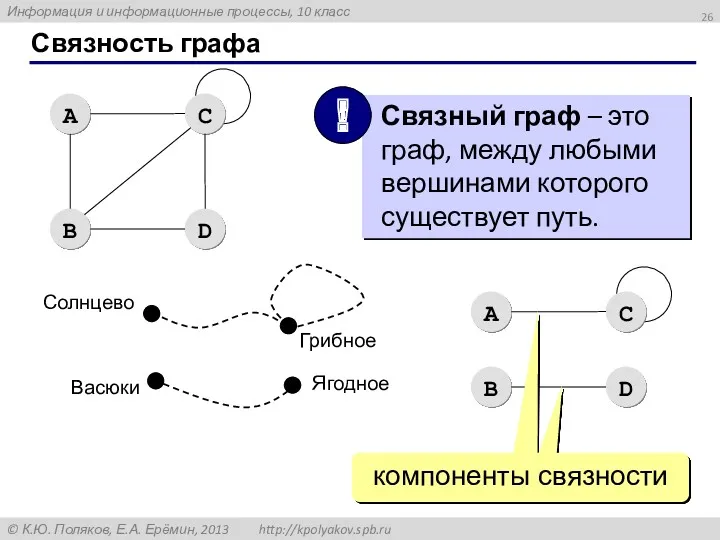
- 26. Связность графа
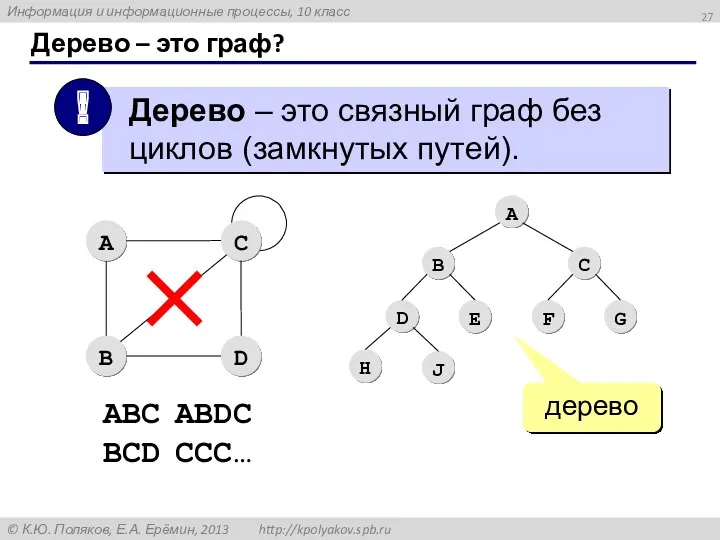
- 27. Дерево – это граф? дерево ABC ABDC BCD CCC…
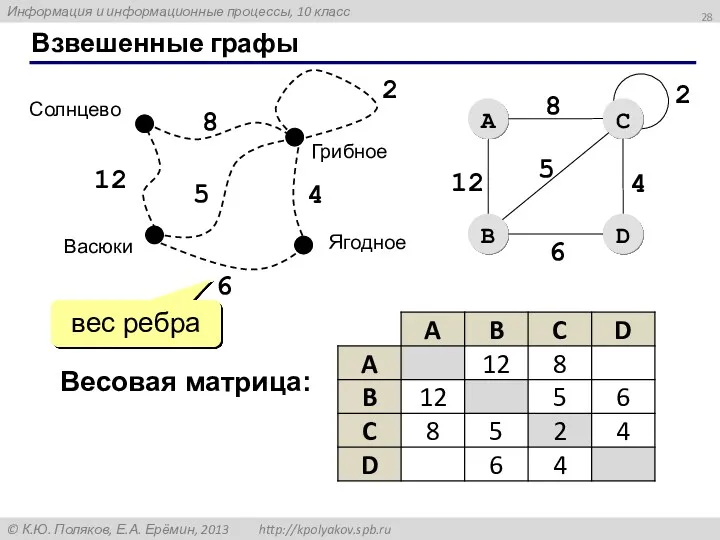
- 28. Взвешенные графы 12 8 2 5 4 6 Весовая матрица: вес ребра
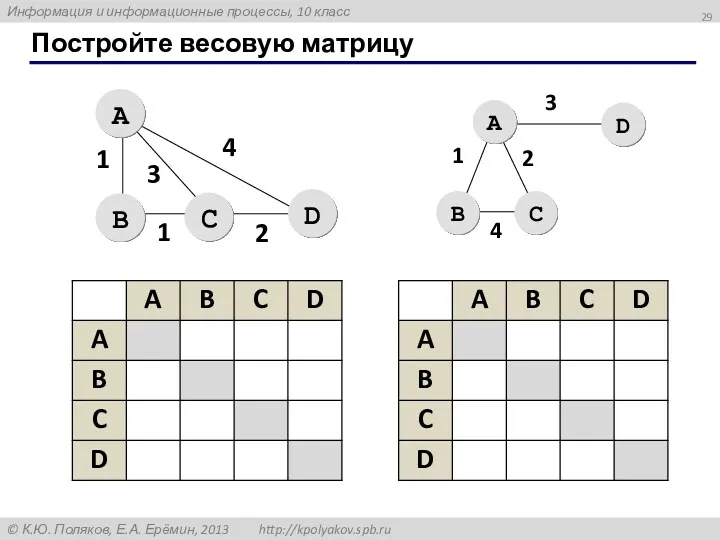
- 29. Постройте весовую матрицу
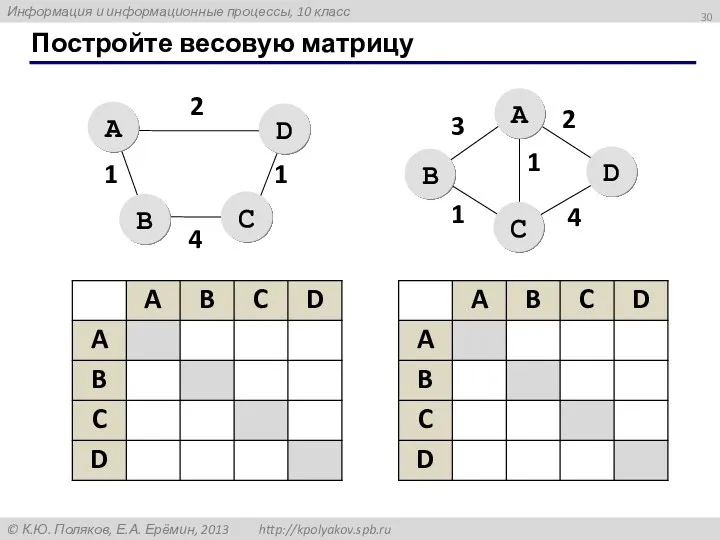
- 30. Постройте весовую матрицу
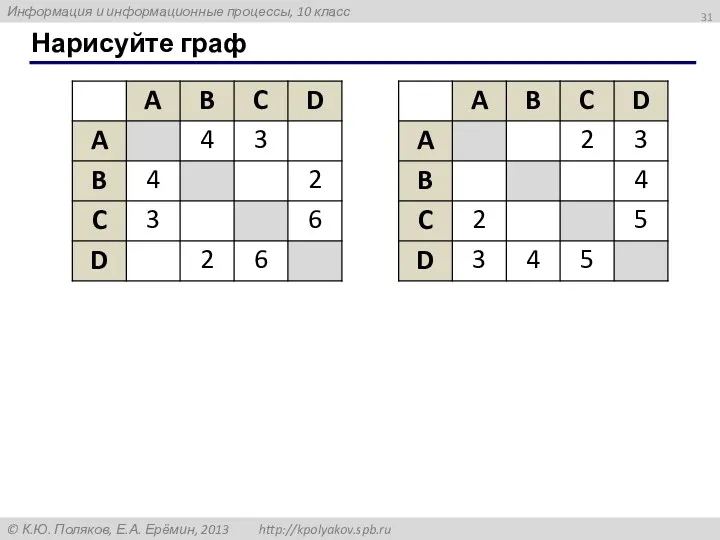
- 31. Нарисуйте граф
- 32. Нарисуйте граф
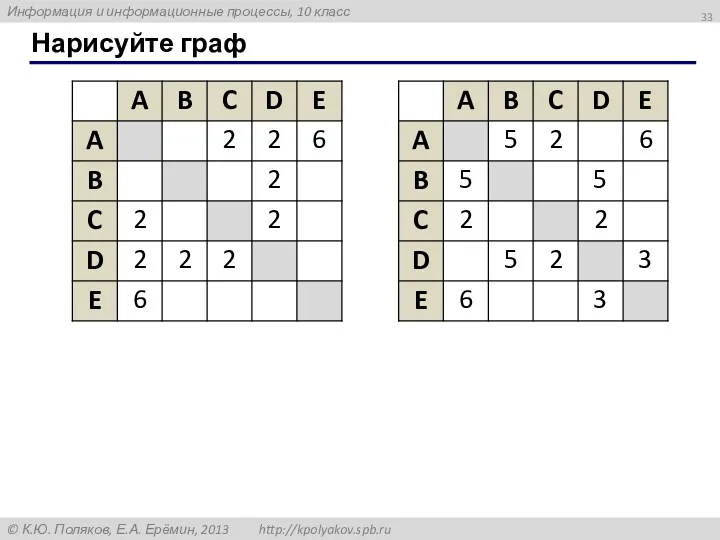
- 33. Нарисуйте граф
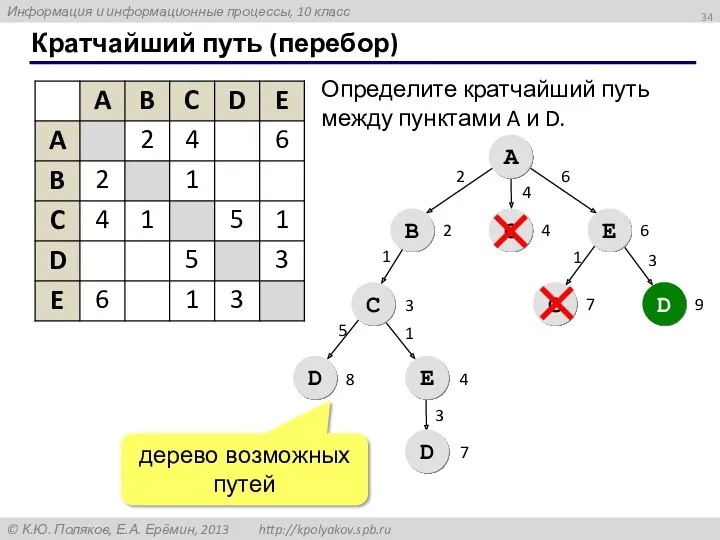
- 34. Кратчайший путь (перебор) A B С E С D С D E D 2 4 6
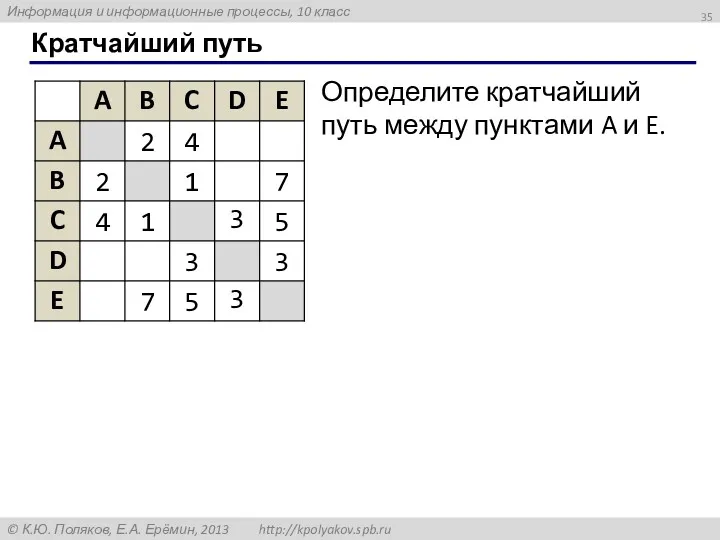
- 35. Кратчайший путь Определите кратчайший путь между пунктами A и E.
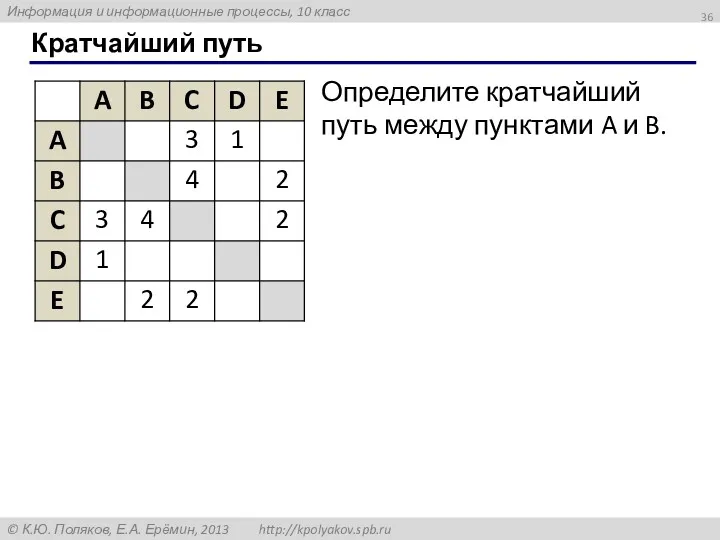
- 36. Кратчайший путь Определите кратчайший путь между пунктами A и B.
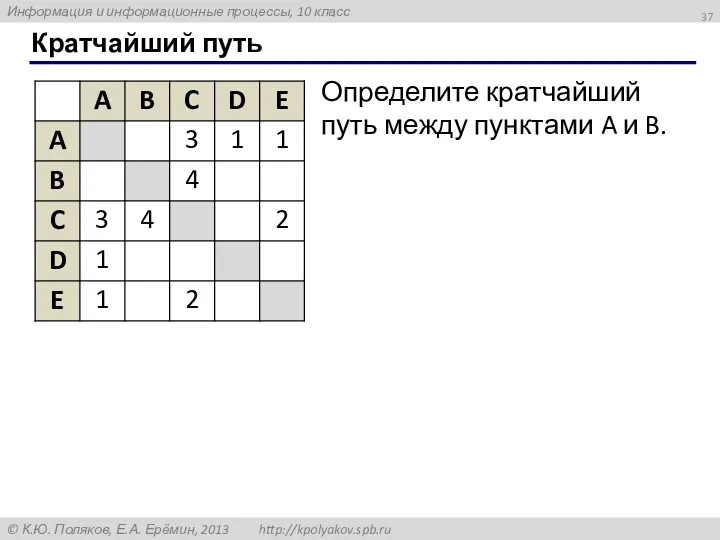
- 37. Кратчайший путь Определите кратчайший путь между пунктами A и B.
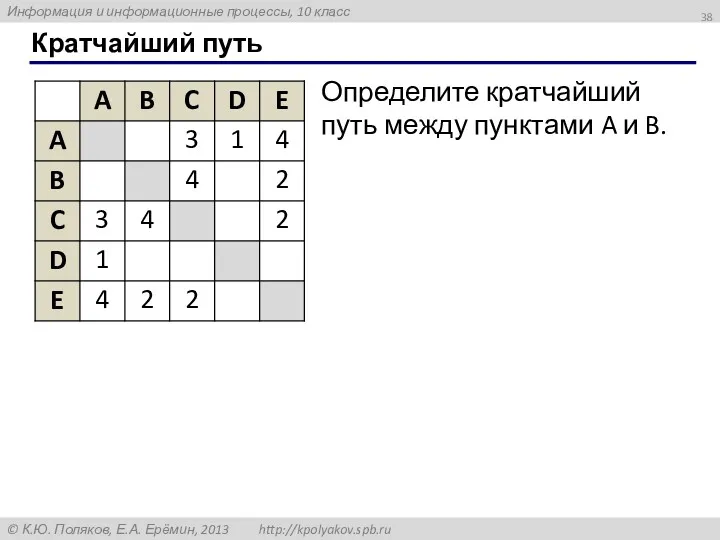
- 38. Кратчайший путь Определите кратчайший путь между пунктами A и B.
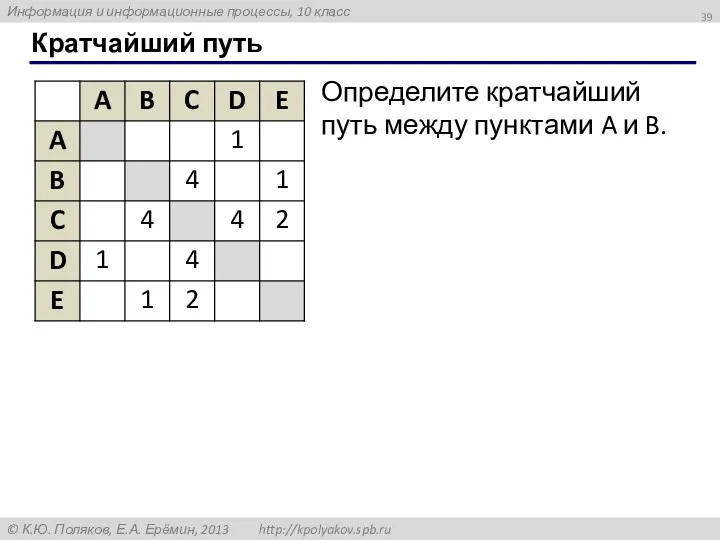
- 39. Кратчайший путь Определите кратчайший путь между пунктами A и B.
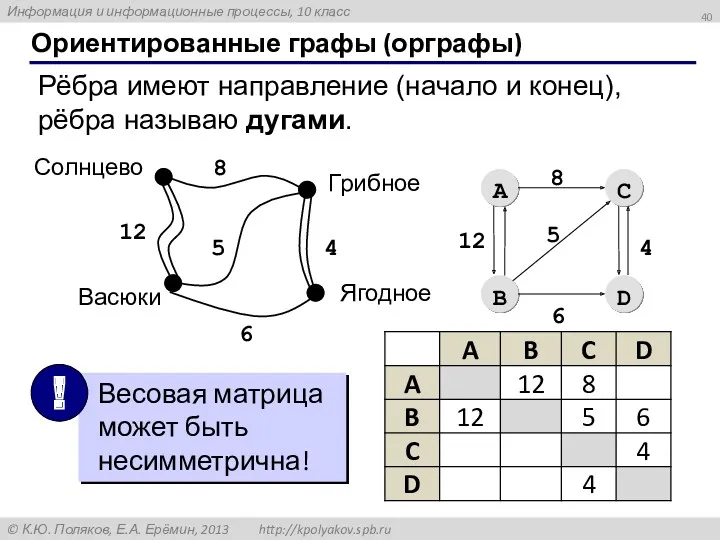
- 40. Ориентированные графы (орграфы) Рёбра имеют направление (начало и конец), рёбра называю дугами.
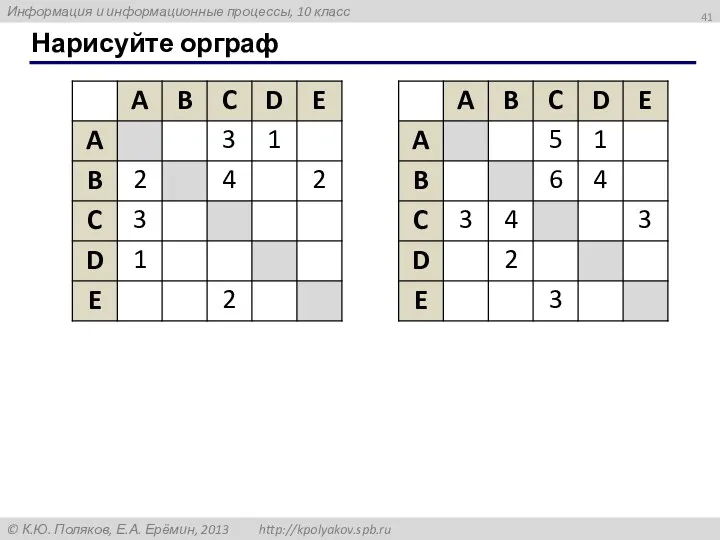
- 41. Нарисуйте орграф
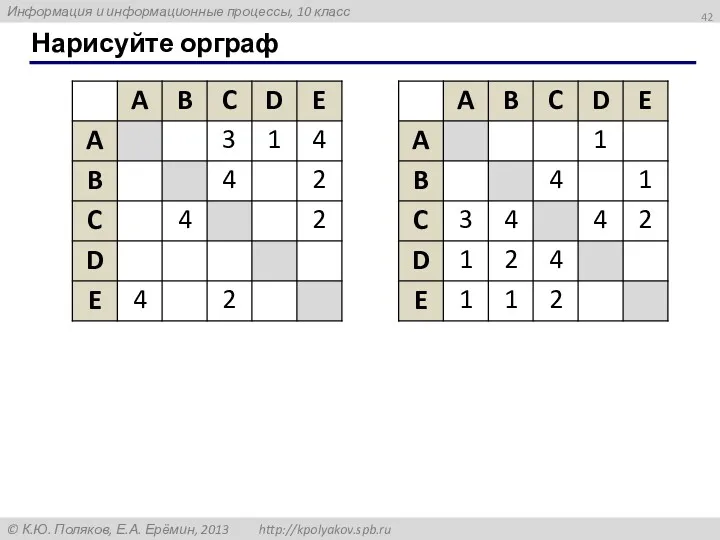
- 42. Нарисуйте орграф
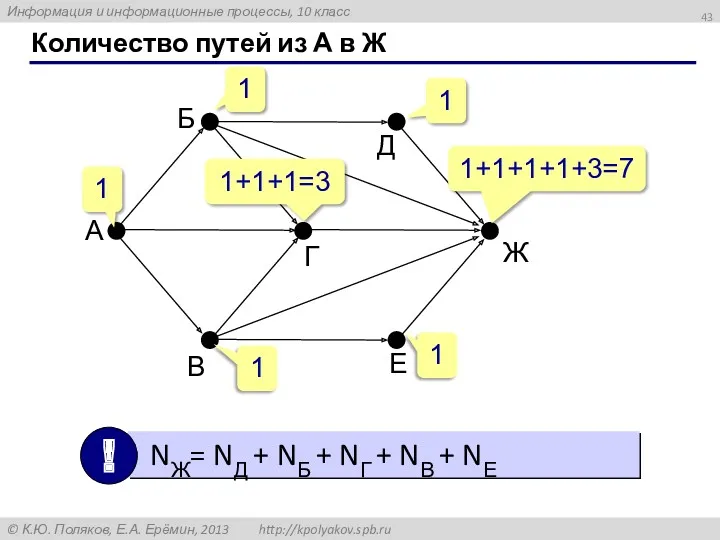
- 43. Количество путей из А в Ж 1 1 1 1+1+1=3 1 1+1+1+1+3=7 1
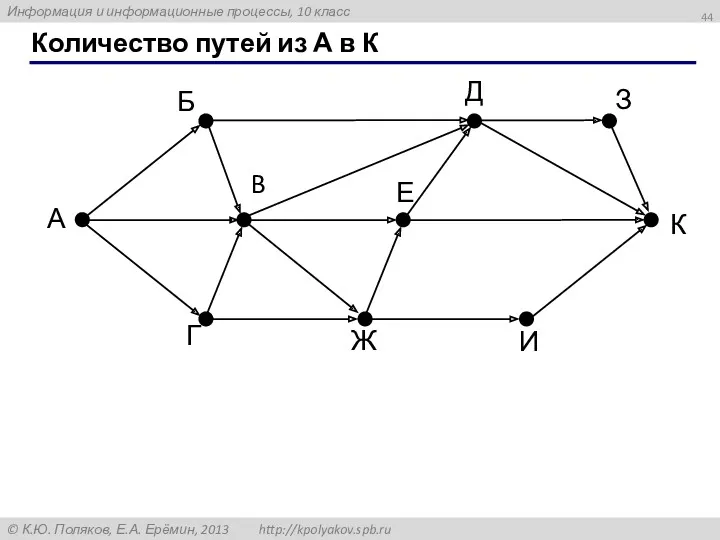
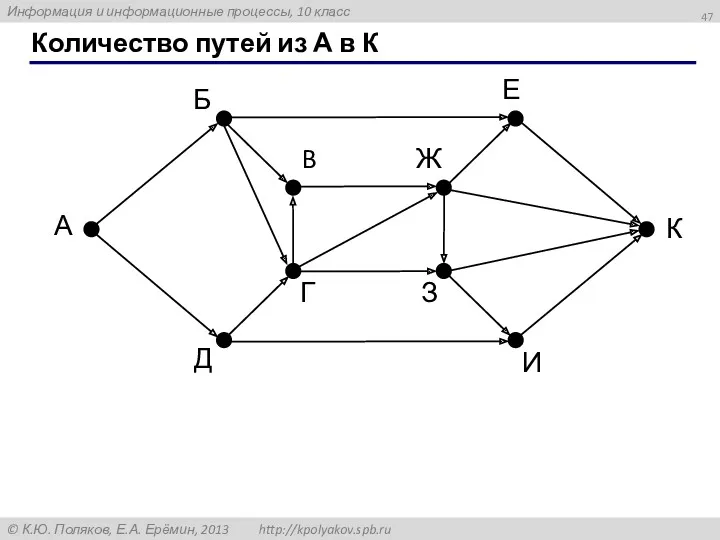
- 44. Количество путей из А в К
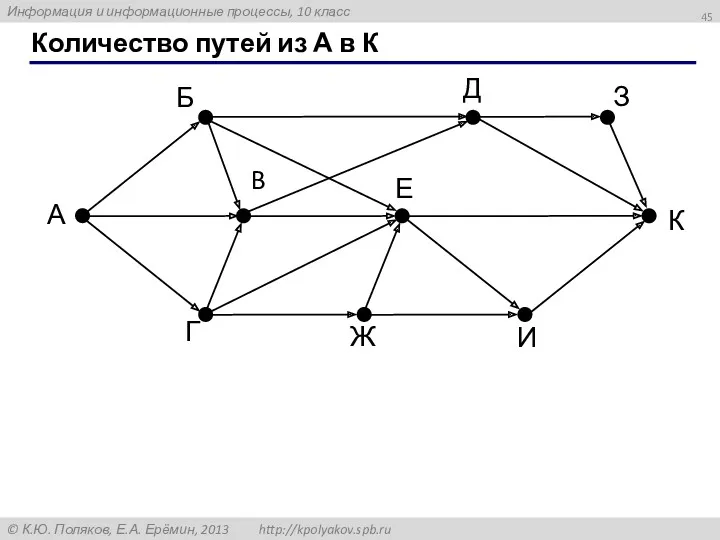
- 45. Количество путей из А в К
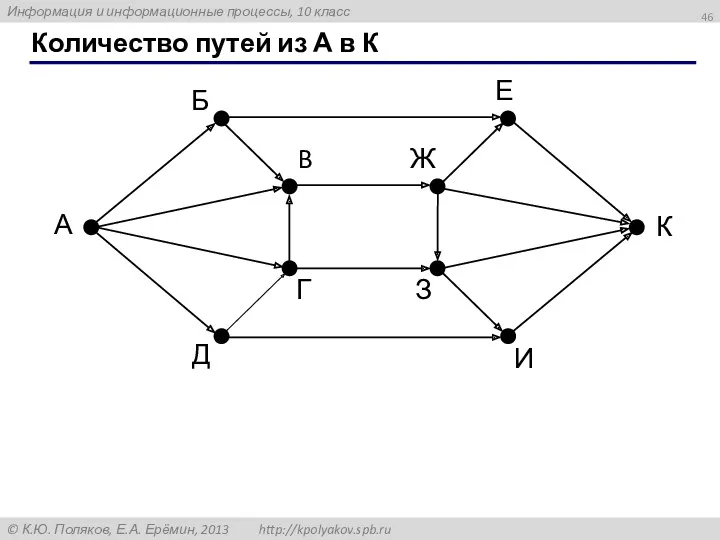
- 46. Количество путей из А в К
- 47. Количество путей из А в К
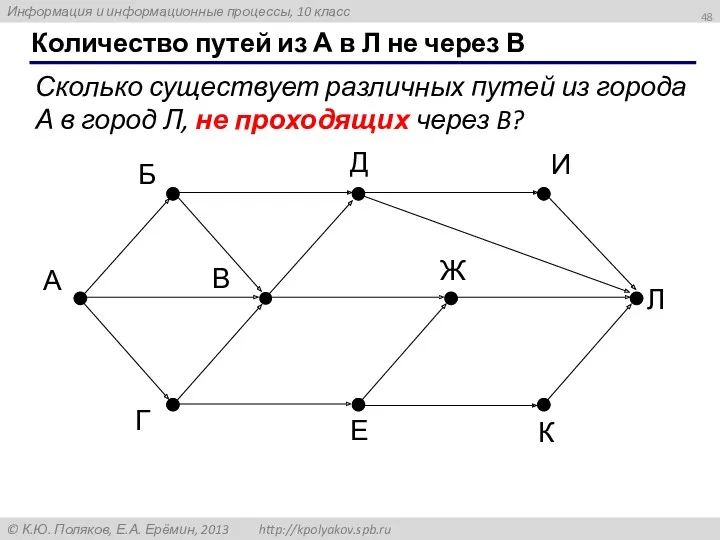
- 48. Количество путей из А в Л не через В А Б В Г Д Е Ж
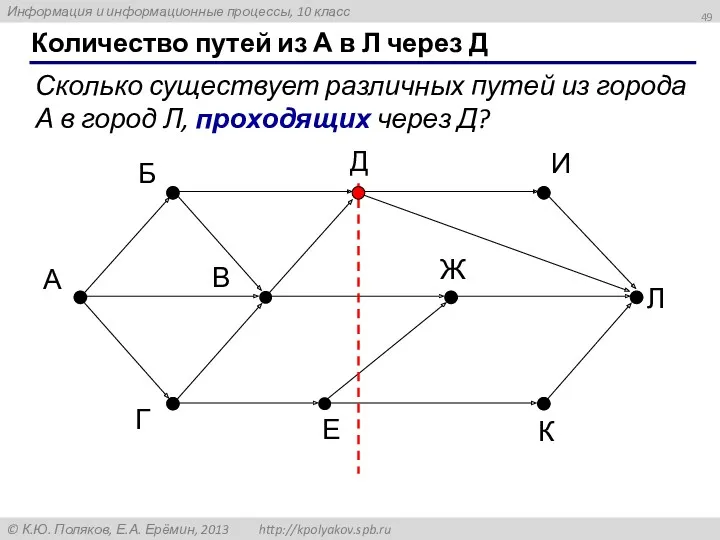
- 49. Количество путей из А в Л через Д А Б В Г Д Е Ж И
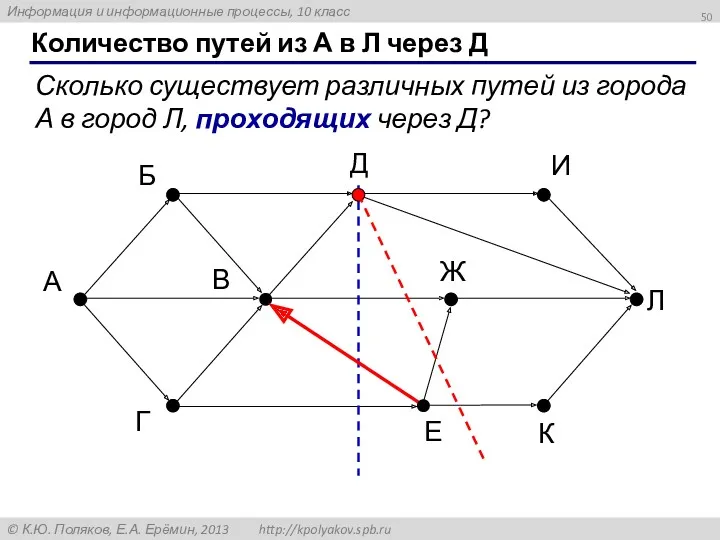
- 50. Количество путей из А в Л через Д Сколько существует различных путей из города А в
- 51. Конец фильма ПОЛЯКОВ Константин Юрьевич д.т.н., учитель информатики ГБОУ СОШ № 163, г. Санкт-Петербург kpolyakov@mail.ru ЕРЕМИН
- 53. Скачать презентацию


















 SQL Server
SQL Server Циклы в Python
Циклы в Python Основы компьютерной графики языка Java. (Занятие 5)
Основы компьютерной графики языка Java. (Занятие 5) Архив журнала Вопросы истории
Архив журнала Вопросы истории Способы применения ПК для перевода текстов
Способы применения ПК для перевода текстов Основы построения VPN
Основы построения VPN Отношения между понятиями
Отношения между понятиями Конкурсное задание Интернет-ресурс
Конкурсное задание Интернет-ресурс Управленческий учет затрат, финансовый результат в прикладном решении 1С:ERP Управление предприятием 2
Управленческий учет затрат, финансовый результат в прикладном решении 1С:ERP Управление предприятием 2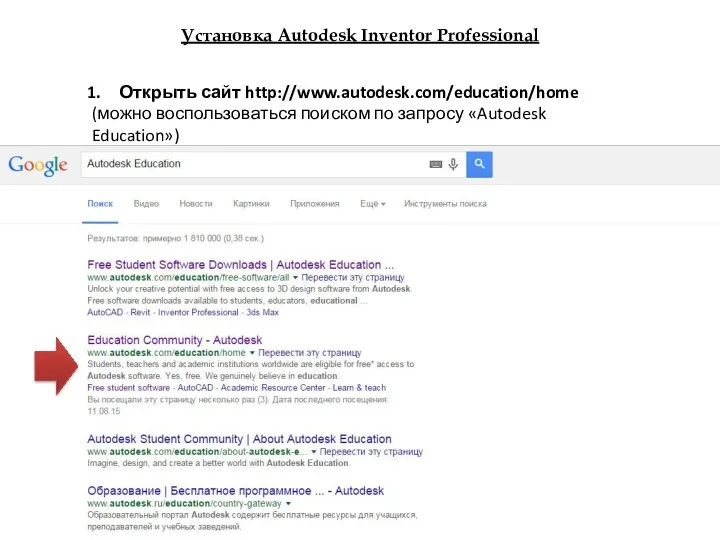 Установка Autodesk Inventor Professional
Установка Autodesk Inventor Professional Искусственный интеллект
Искусственный интеллект Развитие языков программирования. Обзор языков программирования
Развитие языков программирования. Обзор языков программирования Тестирование вёрстки нового сайта ААА моторс
Тестирование вёрстки нового сайта ААА моторс Беспроводные телематические решения для города на базе LPWAN технологии. Презентация решений для городской экономики
Беспроводные телематические решения для города на базе LPWAN технологии. Презентация решений для городской экономики Подготовка к выполнению курсовой работы
Подготовка к выполнению курсовой работы Вспомогательные алгоритмы и подпрограммы. Процедуры
Вспомогательные алгоритмы и подпрограммы. Процедуры Создание структуры базы данных. Семинар 3. Лекция 1. Первое знакомство с базами данных
Создание структуры базы данных. Семинар 3. Лекция 1. Первое знакомство с базами данных Кодирование информации. 5 класс
Кодирование информации. 5 класс Автоматизированная форма бухгалтерского учета
Автоматизированная форма бухгалтерского учета How the Web is changing the world
How the Web is changing the world Микропроцессор
Микропроцессор Компьютердің конструктивті құрылғылары
Компьютердің конструктивті құрылғылары Побудова локальної комп'ютерної мережі
Побудова локальної комп'ютерної мережі Семейство SIMATIC S7
Семейство SIMATIC S7 Lektsia_2-16-Elementy_GIP_3
Lektsia_2-16-Elementy_GIP_3 Программирование (Python)
Программирование (Python) Програмне забезпечення комп’ютерних мереж
Програмне забезпечення комп’ютерних мереж Векторный графический редактор Open office.org Draw
Векторный графический редактор Open office.org Draw