Содержание
- 2. Под кодированием понимают преобразование алфавита источника сообщений A={ai }, ( i = 1,2…,K ) в алфавит
- 3. Совокупность правил, в соответствии с которыми производятся операции преобразования алфавита источника сообщений в кодовые слова, называют
- 4. *
- 5. Кодирование сообщений может преследовать различные цели. Одна из них - представить сообщение в такой системе символов,
- 6. По условиям построения кодовых слов коды делятся на равномерные и неравномерные. Если кодовые слова имеют разную
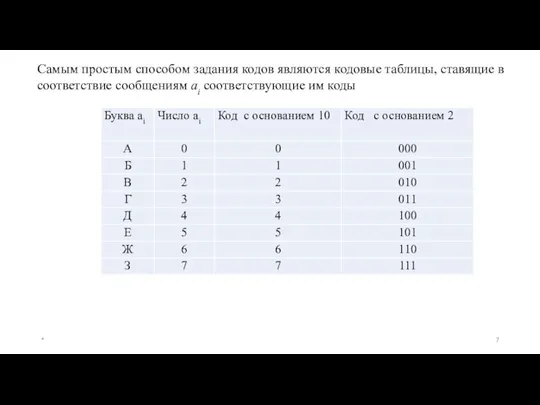
- 7. Самым простым способом задания кодов являются кодовые таблицы, ставящие в соответствие сообщениям ai соответствующие им коды
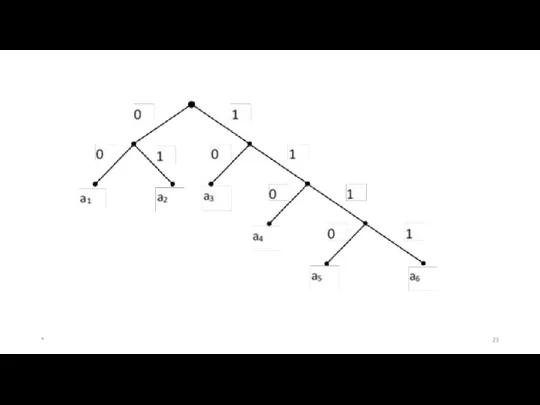
- 8. Другим наглядным способом описания кодов является их представление в виде кодового дерева *
- 9. Для того, чтобы построить кодовое дерево для данного кода, начиная с некоторой точки - корня кодового
- 10. Если исходный алфавит содержит K символов, то для построения равномерного кода с использованием N кодовых символов
- 11. Очевидно, что при различной вероятности появления букв исходного алфавита равномерный код является избыточным, так как энтропия,
- 12. Если i-я буква, вероятность которой Рi, получает кодовую комбинацию длины qi, то средняя длина комбинации Считая
- 13. Чем ближе значение qср к энтропии Н, тем более эффективно кодирование. В идеальном случае, когда qср
- 14. При построении неравномерных кодов необходимо обеспечить возможность их однозначной расшифровки. В равномерных кодах такая проблема не
- 15. Для построения неравномерных кодов, допускающих однозначное декодирование необходимо, чтобы всем буквам алфавита соответствовали лишь листья кодового
- 16. Прием и декодирование неравномерных кодов - процедура гораздо более сложная, чем для равномерных. Возникает вопрос, зачем
- 17. Таким образом, при кодировании сообщений с равновероятными буквами избыточность выбранного (равномерного) кода оказалась равной нулю. Пусть
- 18. В связи с тем, что при кодировании неравновероятных сообщений равномерные коды обладают большой избыточностью, было предложено
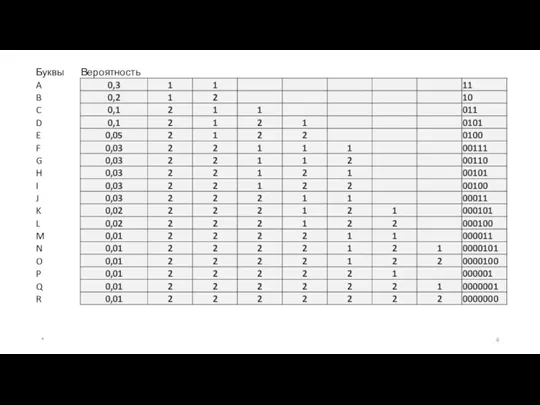
- 19. Первый метод (Метод Р. Фано). Алгоритм сводится к последовательному выполнению следующих ПЯТИ шагов: 1. Буквы алфавита
- 20. 3. Если подгруппы А(0), А(1) состоят более чем из двух букв, то разбиваем множество букв каждой
- 21. 4. Если есть подгруппы, состоящие более чем из одной буквы, то разбиваем каждую из них на
- 22. Рассмотрим следующий пример: Средняя длина для построенного кода qср = 2,44. Соответствующее кодовое дерево имеет вид:
- 23. *
- 24. Полученный код называют еще префиксным множеством. В нашем случае это множество следующее: S = {00, 01,
- 25. ОПЕРАЦИЯ УСЕЧЕНИЯ Рассмотрим кодовое дерево, максимальный порядок концевых вершин которого равен n. Предположим, что вершине а
- 26. Вектор КРАФТА Если S = {w1, w2, ... , wK} – префиксное множество, то можно определить
- 27. Для него справедливо следующее утверждение: если S – какое-либо префиксное множество, то v(S) – вектор Крафта.
- 28. Теорема не утверждает, что любой код с длинами кодовых слов, удовлетворяющими неравенству Крафта, является префиксным. Например,
- 29. Второй метод построения двоичных префиксных кодов (Метод К. Шеннона). 1. Буквы алфавита А упорядочиваем по убыванию
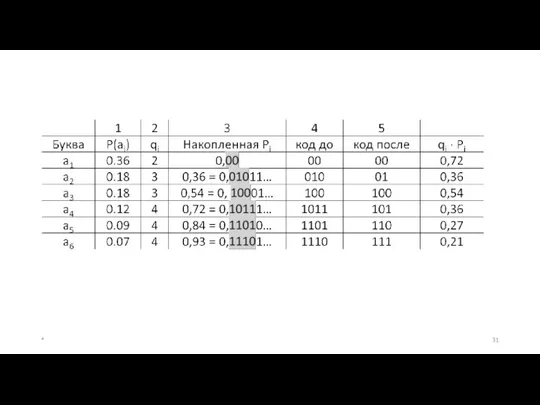
- 30. 4. Находим первые после запятой qi знаков в разложении числа Рi в двоичную дробь: i=1, …,
- 31. *
- 32. Средняя длина для построенного кода qср = 2,46. Соответствующее кодовое дерево до и после усечения имеет
- 33. Методика кодирования Хаффмана (Хаффмэна) Рассмотренные выше алгоритмы кодирования не всегда приводят к хорошему результату, вследствие отсутствия
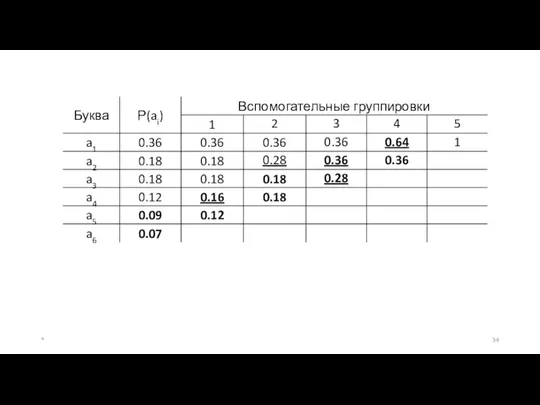
- 34. *
- 35. После этого строится кодовое дерево. а) Корню дерева ставится в соответствие узел с вероятностью, равной 1.
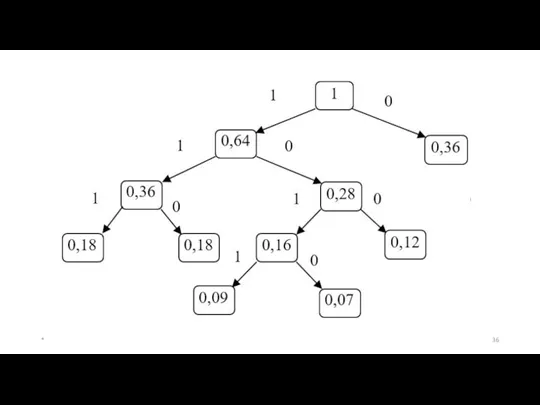
- 36. *
- 37. Процесс кодирования по кодовому дереву осуществляется следующим образом. Одной из ветвей, выходящей из каждого узла, например,
- 38. Средняя длина для построенного кода qср = 2,44, ЭНТРОПИЯ ИСТОЧНИКА В ЭТОМ ПРИМЕРЕ: H(Z) = 2,37
- 39. БЛОЧНОЕ КОДИРОВАНИЕ *
- 40. Можно видеть, что как для кода Хаффмана, так и для кодов Фано и Шеннона среднее количество
- 41. Рассматриваемая теорема Шеннона часто приводится и в другой формулировке: сообщения источника с энтропией Н(Z) всегда можно
- 42. Итак, из теоремы Шеннона следует, что избыточность в последовательностях символов можно устранить, если перейти к кодированию
- 43. Используем метод Шеннона-Фано Буква Вероятность код А 0.7 1 Б 0.3 0 1*0.7+1*0.3=1 двоичн. знаков на
- 44. Буква Вероятность код АА 0.7*0.7=0,49 1 АБ 0.7*0.3=0,21 01 БА 0.3*0.7=0,21 001 ББ 0.3*0.3=0,21 000 1*0.49+2*0.21+3*0.3=1,81
- 45. Недостатки методов эффективного кодирования 1. Различия в длине кодовых комбинаций. Обычно знаки на вход устройства кодирования
- 46. * Задача 1. Для передачи сообщений используется код, состоящий из трех символов, вероятности появления которых равны
- 47. * где p=0.05 - вероятность ошибки. Определить все апостериорные вероятности. Задача 2
- 48. * А может быть передан правильно с вероятностью P(xi , y j )= P( y j
- 50. Скачать презентацию









































 Правовые нормы, относящиеся к информации, правонарушения в информационной сфере
Правовые нормы, относящиеся к информации, правонарушения в информационной сфере Киберспорт и его развитие
Киберспорт и его развитие Матричный калькулятор с использованием Windows Forms
Матричный калькулятор с использованием Windows Forms Поисковая система Яндекс
Поисковая система Яндекс Автоматы и формальные языки
Автоматы и формальные языки Компьютерные вирусы и антивирусные программы
Компьютерные вирусы и антивирусные программы Cмарт (цифровые) города. Энергоэффективная и экологическая направленность цифровых городов. Градостроительство 21 века
Cмарт (цифровые) города. Энергоэффективная и экологическая направленность цифровых городов. Градостроительство 21 века Управление памятью и сборщик мусора в .NET и Rotor 2.0
Управление памятью и сборщик мусора в .NET и Rotor 2.0 Кодування та декодування повідомлень
Кодування та декодування повідомлень Передача информации. Схема передачи информации. Электронная почта
Передача информации. Схема передачи информации. Электронная почта Язык SQL
Язык SQL Элементы алгебры логики. Математические основы информатики
Элементы алгебры логики. Математические основы информатики Автоматизация расчетов массового расхода газа через сужающее отверстие
Автоматизация расчетов массового расхода газа через сужающее отверстие Системы управления сетями и услугами телекоммуникаций
Системы управления сетями и услугами телекоммуникаций Разработка урока по программированию на Бейсике
Разработка урока по программированию на Бейсике Культура оформлення комп’ютерної презентації
Культура оформлення комп’ютерної презентації Информационные технологии в отеле. Система бронирования номеров
Информационные технологии в отеле. Система бронирования номеров M/EEG source analysis
M/EEG source analysis Символ текста (C++). Лекция 9 по основам программирования
Символ текста (C++). Лекция 9 по основам программирования Передача, обработка и хранение информации
Передача, обработка и хранение информации Обзор компьютера
Обзор компьютера Медиа-карта сайтов Красноярского края
Медиа-карта сайтов Красноярского края Перевод чисел в позиционных системах счисления
Перевод чисел в позиционных системах счисления Объектно-реляционная модель данных
Объектно-реляционная модель данных LI-FI световая замена WI-FI
LI-FI световая замена WI-FI Создание 3D модели школы
Создание 3D модели школы Технология Ethernet
Технология Ethernet PowerPoint: как сделать удачную презентацию
PowerPoint: как сделать удачную презентацию