Содержание
- 2. Задача линейного программирования – 3 слайд. Геометрический метод решения ЗЛП – 26 слайд. Задача линейного программирования
- 3. Задача линейного программирования (ЛП) Задачи ЛП – самая обширная часть оптимизационных (примерно 70%)
- 4. Этапы построения математической модели Определение переменных задачи. Представление ограничений в виде линейных уравнений или неравенств. Задание
- 5. Классические задачи линейного программирования Задача технического контроля (слайд 6); Транспортная задача (слайд 13 ); Задача о
- 6. Задача технического контроля Примечание: ОТК – Отдел Технического Контроля
- 7. В ОТК некоторой фирмы работают контролеры 1 и 2 разрядов (К1 и К2); Норма выработки ОТК
- 9. Построение модели
- 10. Построение модели
- 11. 3. Задание целевой функции
- 12. Вся задача технического контроля может быть сформулирована следующим образом.
- 13. Транспортная задача Или задача о рациональном перевозе однородных продуктов из пунктов производства в пункты потребления.
- 15. Математическая модель задачи
- 16. Задача о диете Или задача о составлении рациона
- 18. Математическая модель задачи
- 19. Задача об использовании сырья
- 21. Исходные данные задачи Представим исходные данные в виде таблицы
- 23. Исходные данные для кондитерской Тогда после перехода к условным единицам получим таблицу
- 24. Математическая модель задачи
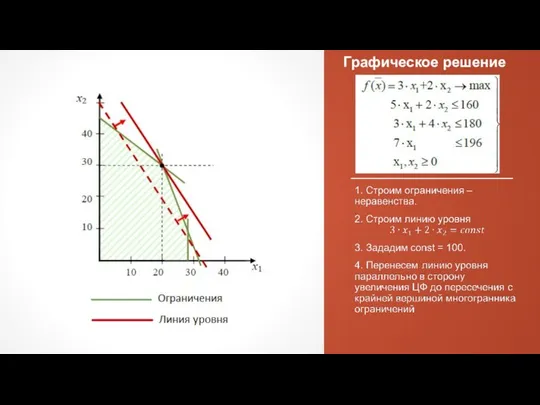
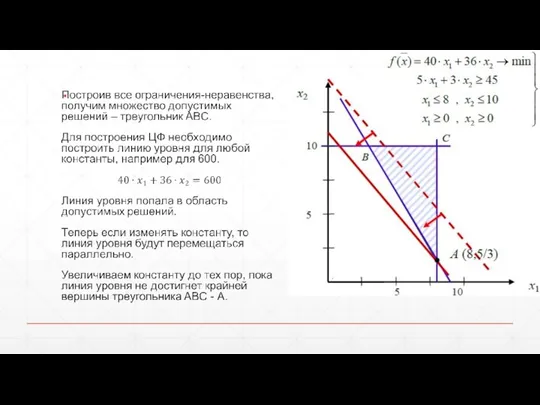
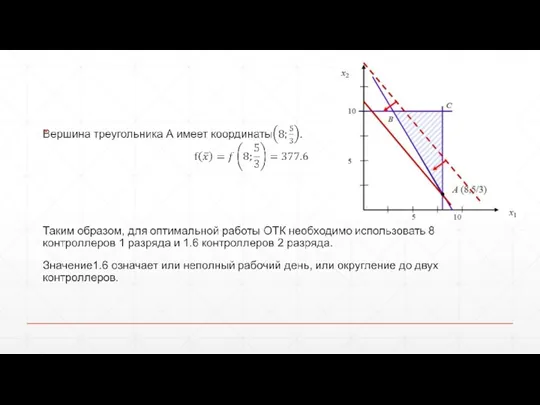
- 25. Графическое решение
- 26. Геометрический метод решения ЗЛП Решим геометрическим методом задачу технического контроля:
- 29. Частные случаи геометрических решений
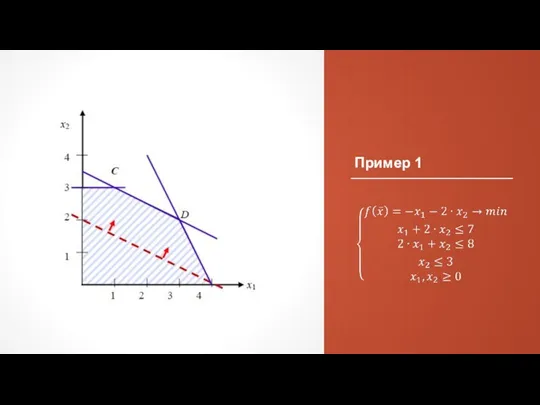
- 30. Пример 1
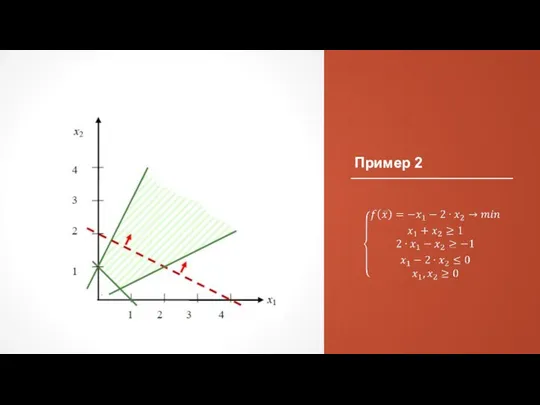
- 31. Пример 2
- 32. Задача линейного программирования в стандартной форме
- 34. Матрично–векторная запись
- 35. Приведение ЗЛП к стандартному виду
- 36. Преобразования неравенств
- 37. Преобразования неравенств Преобразуем неравенства из задачи об использовании сырья добавив во все три уравнения остаточную переменную.
- 38. Приведение ЗЛП к стандартному виду
- 39. Приведение ЗЛП к стандартному виду
- 40. Пример приведения ЗЛП к стандартному виду
- 41. Перепишем задачу ЛП с учетом новых переменных и замен:
- 42. Симплекс метод решения ЗЛП
- 43. Запишем задачу линейного программирования в стандартной форме в развернутом виде: Число уравнений системы меньше числа неизвестных
- 44. Метод Гаусса – Жордана Основная идея метода состоит в сведении m уравнения с n неизвестными к
- 45. Базисные и свободные переменные
- 46. Выразим из предыдущей системы базисные переменные: Из этой системы можно получить решение для базисных переменных, присваивая
- 47. Базисное решение Опорный план vbnvbg
- 48. Метод последовательного исключения переменных (метод Гаусса) Метод Гаусса состоит из двух этапов: Прямой ход Обратный ход
- 49. Прямой ход
- 50. Прямой ход
- 51. Обратный ход
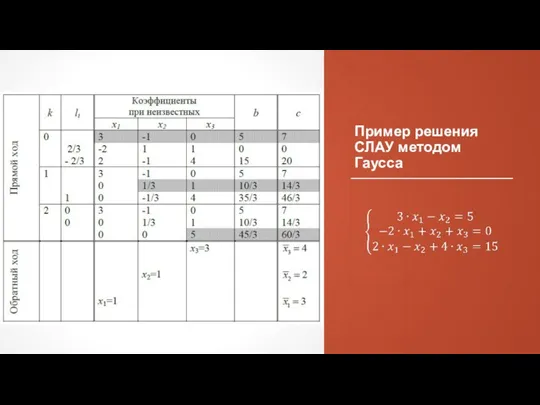
- 52. Пример решения СЛАУ методом Гаусса
- 54. Метод главных элементов Применяется в случаях, когда главные диагональные элементы системы уравнений в результате преобразований получаются
- 55. Основная идея метода главных элементов
- 56. Основная идея метода главных элементов В результате составляем новую систему уравнений из вычеркнутых строк. Полученная матрица
- 57. Пример решения СЛАУ методом Гаусса с выбором главного элемента
- 58. Симплекс метод
- 59. Алгоритм симплекс метода Выбор начального опорного плана. Переход от начального опорного плана к другому опорному плану
- 60. Смежный опорный план Смежным опорным планом называют план, отличающийся от текущего лишь одной переменной. Для получения
- 61. Составим симплекс – таблицу для задачи использования ресурсов. Для этого запишем - задачу в каноническом виде
- 62. Начальный опорный план
- 63. I. Нахождение начального опорного плана
- 64. II. Нахождение смежного опорного плана Необходимо одну переменную из свободных перевести в базис, так, чтобы целевая
- 66. Лемма 1
- 67. Лемма 2
- 69. III. Приведение системы к каноническому виду
- 70. Шаг 1
- 71. Шаг 2
- 72. Шаг 3
- 73. Шаг 4
- 74. Полная симплекс таблица
- 75. Замечание
- 76. Метод искусственного базиса
- 79. Пример
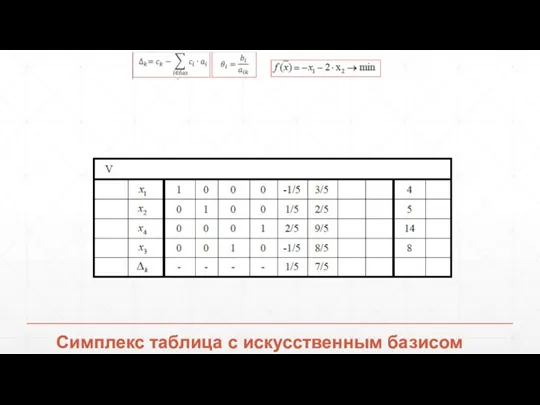
- 81. Симплекс таблица с искусственным базисом
- 82. Симплекс таблица с искусственным базисом
- 83. Симплекс таблица с искусственным базисом
- 85. Этапы метода искусственного базиса
- 86. Этапы метода искусственного базиса
- 88. Двойственность задач линейного программирования
- 89. Определение двойственности Для любой задачи линейного программирования существует некоторая другая задача линейного программирования, решение которой тесно
- 90. Прямая и двойственная задачи
- 91. Теорема 1
- 92. Теорема 2
- 93. Сравнение прямой и двойственной задачи
- 94. В исходной задаче В двойственной
- 95. Число ограничений и переменных В исходной задаче n – переменных; m – ограничений. В двойственной m
- 96. Правые части ограничений – это коэффициенты целевой функции двойственной задачи
- 97. Знаки ограничений и цель задачи меняются на противоположные В исходной задаче В двойственной
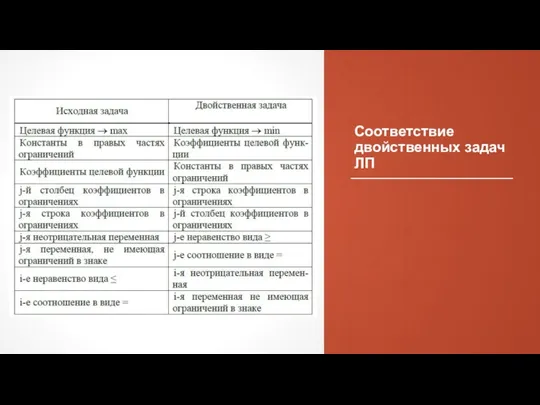
- 98. Соответствие двойственных задач ЛП
- 99. Пример
- 100. Симплекс таблица двойственной задачи
- 101. Таким образом, получен следующий оптимальный план двойственной задачи: Для получения оптимального решения прямой задачи воспользуемся соотношением
- 103. Экономическая трактовка двойственности Если прямую задачу: рассматривать, как задачу об использовании сырья (ресурсов), то параметры задачи
- 104. Экономический смысл переменных
- 105. Тогда стоимость всех ресурсов А стоимость всех затраченных ресурсов, идущих на выпуск единицы j-ой продукции не
- 107. Скачать презентацию
































































































 Информационные технологии
Информационные технологии Системи управління базами даних: основи побудови та моделі організації
Системи управління базами даних: основи побудови та моделі організації Влияние международных IT-компаний на российский рынок
Влияние международных IT-компаний на российский рынок Autodesk inventor система автоматизированного проектирования. Работа в режиме Экскиз. Основные группы команд
Autodesk inventor система автоматизированного проектирования. Работа в режиме Экскиз. Основные группы команд История развития систем искусственного интеллекта
История развития систем искусственного интеллекта Лекция 1. Основы программной инженерии. Понятие программной инженерии. Стандарты программной инженерии
Лекция 1. Основы программной инженерии. Понятие программной инженерии. Стандарты программной инженерии Компьютер и здоровье школьников
Компьютер и здоровье школьников Сетевые экраны
Сетевые экраны Full application. Voice changer
Full application. Voice changer Принципы обработки информации компьютером. Арифметические и логические основы работы компьютера
Принципы обработки информации компьютером. Арифметические и логические основы работы компьютера Настройка информационной системы домена
Настройка информационной системы домена История вычислительной техники
История вычислительной техники Процедуры и функции
Процедуры и функции Геоинформационная система Горизонт
Геоинформационная система Горизонт Персональный компьютер
Персональный компьютер Управление исполнителем чертёжник
Управление исполнителем чертёжник Анімація. Переміщення по кадрах. Шкала часу. Попередній перегляд анімації. Урок №16
Анімація. Переміщення по кадрах. Шкала часу. Попередній перегляд анімації. Урок №16 Специфика работы государственных институтов в социальных медиа
Специфика работы государственных институтов в социальных медиа Взаимодействие процессов: синхронизация, тупики
Взаимодействие процессов: синхронизация, тупики Онлайн-доска. Веб-программирование
Онлайн-доска. Веб-программирование Программирование на Java 2
Программирование на Java 2 Программное обеспечение компьютера
Программное обеспечение компьютера Продаж трафіку
Продаж трафіку Использование логических функций Microsoft Excel
Использование логических функций Microsoft Excel Точні та наближені алгоритми мінімізації числа виконавців при заданих директивних термінах
Точні та наближені алгоритми мінімізації числа виконавців при заданих директивних термінах Оцінка курсів у системі Moodle
Оцінка курсів у системі Moodle Подготовка к ГИА по информатике
Подготовка к ГИА по информатике Создание многотабличной БД. Практическая работа № 19
Создание многотабличной БД. Практическая работа № 19