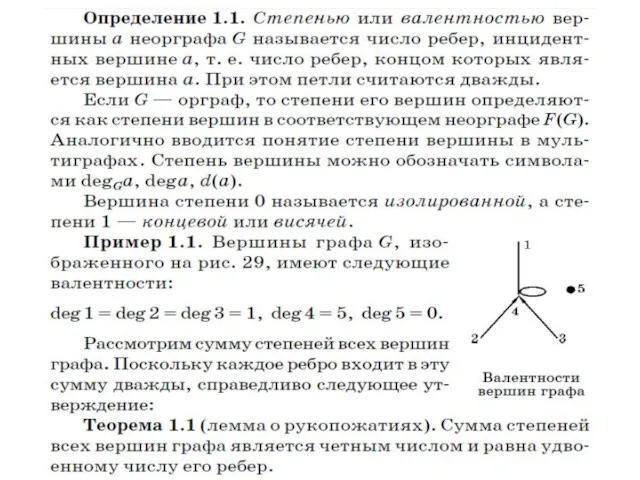
Гамильтонов граф представляет собой граф, который содержит гамильтонов цикл. При этом гамильтоновым
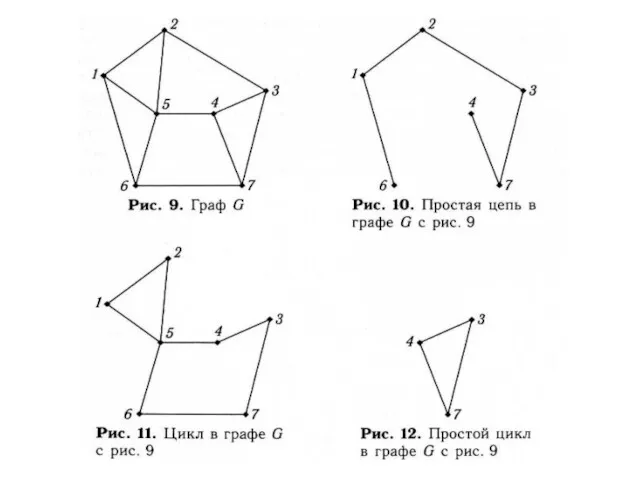
циклом является такой цикл (замкнутый путь), который содержит все вершины (точки) данного графа.
Гамильтонов путь является простым путём (путём без петель), проходящим через каждую вершину графа ровно один раз. Гамильтонов путь отличается от цикла тем, что у пути начальные и конечные точки могут не совпадать, в отличие от цикла. Гамильтонов цикл является гамильтоновым путём.
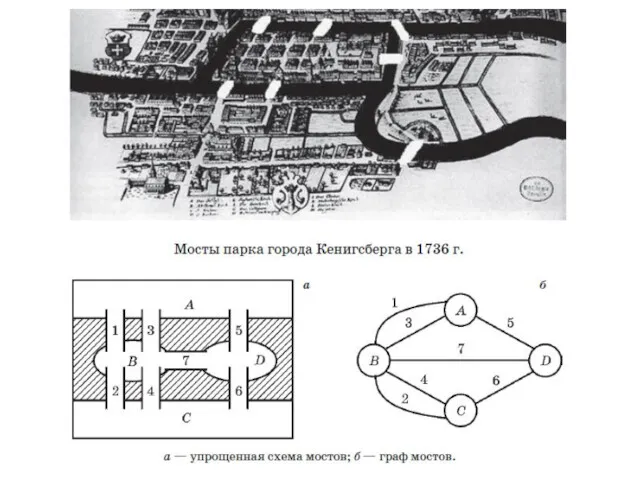
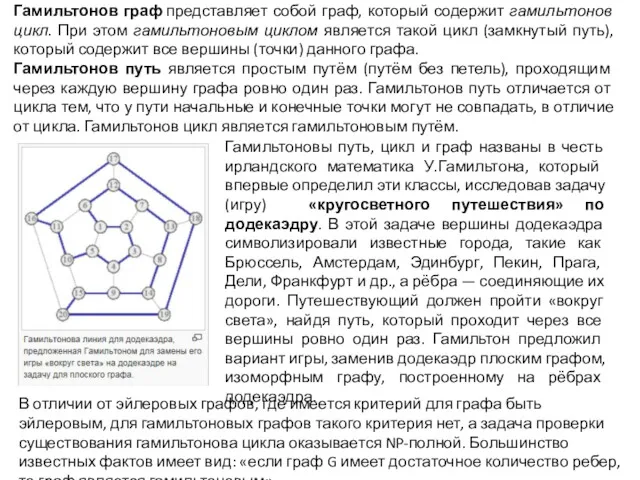
Гамильтоновы путь, цикл и граф названы в честь ирландского математика У.Гамильтона, который впервые определил эти классы, исследовав задачу (игру) «кругосветного путешествия» по додекаэдру. В этой задаче вершины додекаэдра символизировали известные города, такие как Брюссель, Амстердам, Эдинбург, Пекин, Прага, Дели, Франкфурт и др., а рёбра — соединяющие их дороги. Путешествующий должен пройти «вокруг света», найдя путь, который проходит через все вершины ровно один раз. Гамильтон предложил вариант игры, заменив додекаэдр плоским графом, изоморфным графу, построенному на рёбрах додекаэдра.
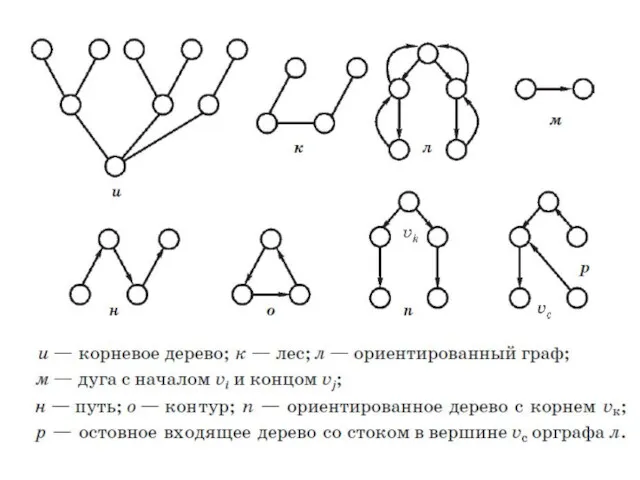
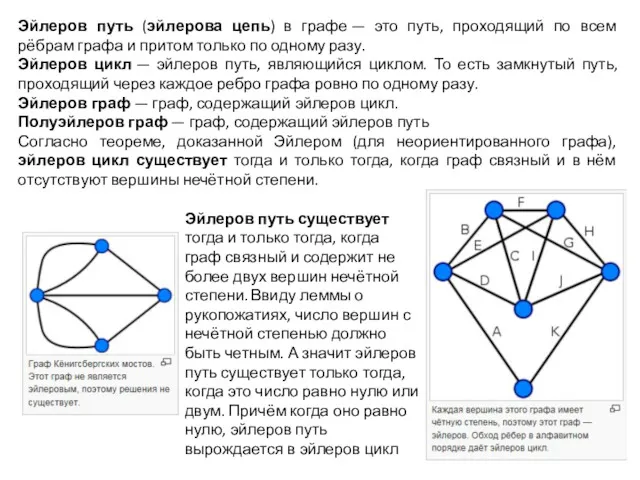
В отличии от эйлеровых графов, где имеется критерий для графа быть эйлеровым, для гамильтоновых графов такого критерия нет, а задача проверки существования гамильтонова цикла оказывается NP-полной. Большинство известных фактов имеет вид: «если граф G имеет достаточное количество ребер, то граф является гамильтоновым».














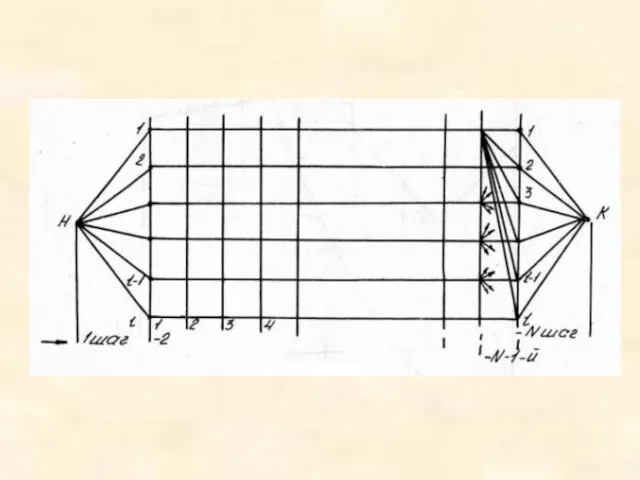

 Текстовая информация
Текстовая информация Установка и настройка Apache и PHP
Установка и настройка Apache и PHP Презентация Состав объектов, 7 класс
Презентация Состав объектов, 7 класс Фактологические жанры PR-текстов
Фактологические жанры PR-текстов Алгоритмы. Свойства и формы представления
Алгоритмы. Свойства и формы представления Инструкция по запуску дистанционных курсов
Инструкция по запуску дистанционных курсов Эффективное использование инструментов разработки веб-страниц
Эффективное использование инструментов разработки веб-страниц Основные понятия и определения информатики
Основные понятия и определения информатики Перезапуск официального сайта: этапы и предложения
Перезапуск официального сайта: этапы и предложения Пользователи Instagram
Пользователи Instagram Ғаламтор, әлеуметтік желілердің жасөспірімдердің қылмысына қатысы
Ғаламтор, әлеуметтік желілердің жасөспірімдердің қылмысына қатысы Прототип мобильного приложения для обучения правильной технике свинга при помощи AI
Прототип мобильного приложения для обучения правильной технике свинга при помощи AI Работа с графическими объектами в текстовом реакторе
Работа с графическими объектами в текстовом реакторе C# decision and iteration constructs
C# decision and iteration constructs Публичная кадастровая карта
Публичная кадастровая карта Рекламные пакеты Турбопромо
Рекламные пакеты Турбопромо Информационные системы управления персоналом. Лекция 1
Информационные системы управления персоналом. Лекция 1 Б-Безопасность ACL, NAT, VPN
Б-Безопасность ACL, NAT, VPN Курс Базы данных. Программирование на языке PL/SQL. Часть 2
Курс Базы данных. Программирование на языке PL/SQL. Часть 2 Проектування у графічному редакторі Sweet Нome 3D
Проектування у графічному редакторі Sweet Нome 3D Программирование на языке Си. Простейшие программы
Программирование на языке Си. Простейшие программы Представление числовой информации с помощью систем счисления (1). 8 класс
Представление числовой информации с помощью систем счисления (1). 8 класс Сервис Отвечает аудитор
Сервис Отвечает аудитор Основные инструменты графического редактора
Основные инструменты графического редактора Числа в памяти компютера
Числа в памяти компютера Программирование ветвлений на Паскаль. Повторение
Программирование ветвлений на Паскаль. Повторение Табличная форма представления информации
Табличная форма представления информации Оценка максимально достижимого параллелизма и масштабируемости параллельных вычислений
Оценка максимально достижимого параллелизма и масштабируемости параллельных вычислений