Содержание
- 2. Множина. Елементи множин Множина – це деяка сукупність об’єктів (предметів, ідей, понять), що розглядається як єдине
- 3. Позначення Множини позначають заголовними, а елементи множин - рядковими латинськими буквами або рядковими латинськими буквами з
- 4. Позначення Приналежність елемента множини позначається символом ∈: a ∈ A (читається: елемент а належить множині А).
- 5. Позначення Приклад. A = {D,C}, D={a, b}, C={c, d, e}. При цьому D∈A, C∈A, проте a∉A
- 6. Скінчені і нескінчені множини Множина називається скінченною, якщо вона містить скінченну кількість елементів і нескінченною, якщо
- 7. Упорядковані множини Упорядкованою вважають таку множину, у якій є важливим порядок слідування елементів. Наприклад, упорядкованою є
- 8. Способи задання множин Перерахуванням елементів А = {a1, a2,... , an}. Приклад. Множина студентів-відмінників у групі
- 9. Способи задання множин Через взначальну властивість Множина Х = {х | Р(x)}, где Р(х) означає, що
- 10. Способи задання множин Рекурсією графіком (таблицею) Множина значень рекурсивної функції є рекурсивно - заданою множиною F={f1,
- 11. Підмножина Множина А, усі елементи якої належать множині В, називають підмножинами множини В. Позначення: A⊂B; A⊆B.
- 12. Рівність множин Неупорядковані множини рівні (рівнопотужні), якщо вони містять однаковий набір елементів. Позначають: A=B. Якщо множини
- 13. Рівність множин А=В тоді і тільки тоді, якщо із умови x∈A слідує x∈B та з умови
- 14. Рівність множин Приклад. Нехай задано множини: A={Іванов, Петров, Сидоров}; B={Іванов, Петров, Сидоров}. A=B, якщо йдеться про
- 15. Рівність множин Приклад. Нехай A – множина остач, що отримуються при послідовному діленні натуральних чисел {3,
- 16. Потужність множин Число елементів у скінченній множині М називають потужністю М і позначають |M|. Приклад. Нехай
- 17. Строге і нестроге включення Нестроге включення позначають А⊆В, та означає, що А – підмножина множини В,
- 18. Строге і нестроге включення Виконання співвідношень А ⊆ В і В ⊆ А є можливим за
- 19. Строге і нестроге включення Приклад. X – множина студентів групи І, Y – множина відмінників групи
- 20. Універсальна множина Універсальна множина − це така множина, що містить всі можливі (допустимі) підмножини (елементи). Універсальна
- 21. Порожня множина Порожньою називають таку множину, яка не містить ніяких елементів. Порожня множина позначається спеціальним символом
- 22. Порожня множина Порожня множина - це також множина, тому, якщо деяка множина A не містить жодного
- 23. Множина-степінь (булеан) Множина всіх підмножин множини X називається множиною-степенем X або булеаном і позначається P (X).
- 24. Геометрична інтерпретація множин : діаграми Венна Побудова діаграм Венна полягає в поділі площини на 2n підмножин
- 25. Діаграми Венна для двох множин Діаграма Венна для двох множин A і B виглядає таким чином.
- 26. Діаграми Венна для трьох множин Діаграма Венна для трьох множин A, B і C виглядає таким
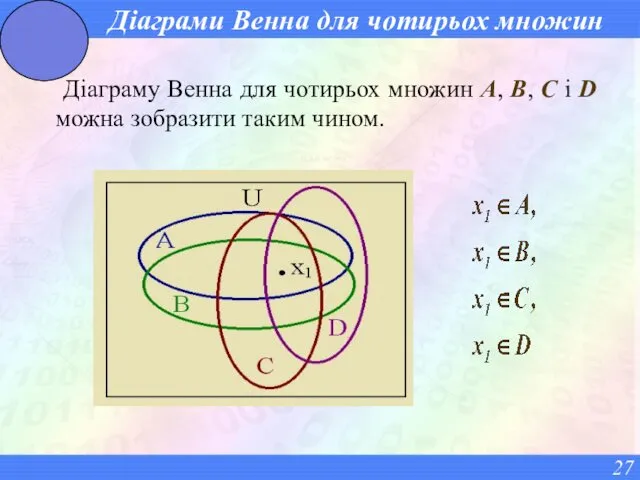
- 27. Діаграми Венна для чотирьох множин Діаграму Венна для чотирьох множин A, B, C і D можна
- 28. Кола (круги) Ейлера Індивідуальні відношення між заданими множинами зображують за допомогою кругів Ейлера (www.youtube.com/watch?v=unXIsqKQLOg). А =
- 29. Алгебра множин Множина 2U всіх підмножин універсальної множини U, із заданими на ній чотирма операціями, складають
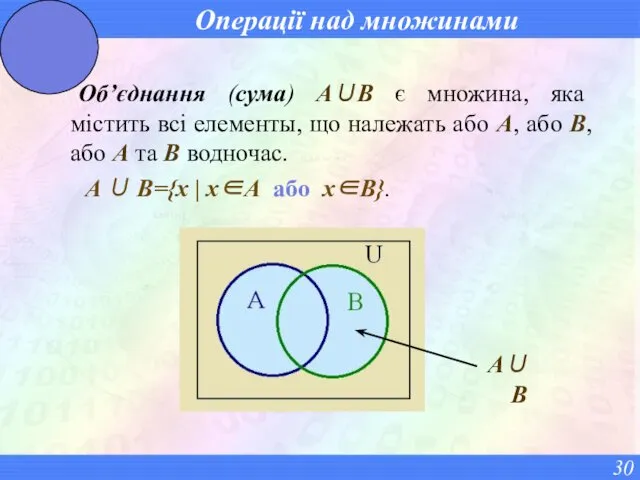
- 30. Операції над множинами Об’єднання (сума) A∪B є множина, яка містить всі елементы, що належать або A,
- 31. Операції над множинами Приклад . Нехай дано множини: А={a, b, m}; В={m, n, c, p}. А∪В=
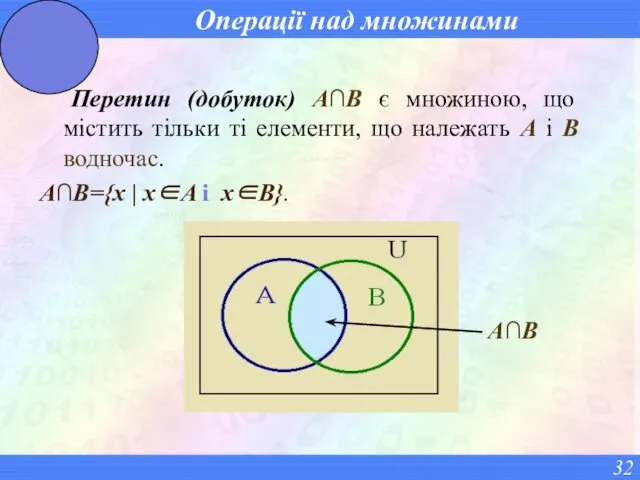
- 32. Операції над множинами Перетин (добуток) A∩B є множиною, що містить тільки ті елементи, що належать A
- 33. Операції над множинами Приклад . Нехай дано множини: А={a, b, m}; В={m, n, c, p}. А∩В
- 34. Операції над множинами Доповнення (заперечення) Ā ( “не А”) є множиною U\A. = {x | x
- 35. Операції над множинами Приклад . Z = {…,-2,-1,0,1,2,…}. У цій задачі U=Z. нехай Z- – множина
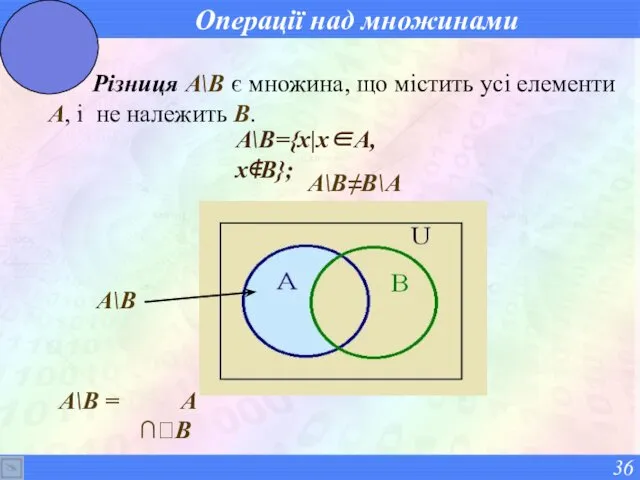
- 36. Операції над множинами Різниця A\B є множина, що містить усі елементи A, і не належить B.
- 37. Операції над множинами Приклад. Нехай дано множини: А={a, b, m}; В={m, n, c, p}. А \
- 38. Пріоритет операцій в алгебрі множин Пріоритет операцій в алгебрі множин такий: 1. A 2. A∩B 3.
- 39. Пріоритет операцій в алгебрі множин Приклад. Розставити дужки (визначити послідовність виконання операцій) у формулі: E=A\B∪ (A)∩D\B.
- 40. Закони алгебри множин 1. Комутативні закони A∪B=B∪A A∩B=B∩A 2. Асоціативні закони A∪(B∪C)=(A∪B)∪C A∩(B∩C)=(A∩B)∩C 3. Дистрибутивні закони
- 41. Закони алгебри множин 4. Властивості порожньої та універсальної множин
- 42. Закони алгебри множин 5. Закони ідемпотентності A∪A=A A∩A=A 6. Закон інволюції (подвійного заперечення) 7. Закон заперечення
- 43. Закони алгебри множин 9. Закон елімінації (поглинання) A∩(A∪B)=A A∪(A∩B)=A 10. Закони де Моргана.
- 44. Закони алгебри множин Приклад. Довести за допомогою діаграм Венна дистрибутивний закон. А∩ (В∪С)=(А∩В)∪(А∩С).
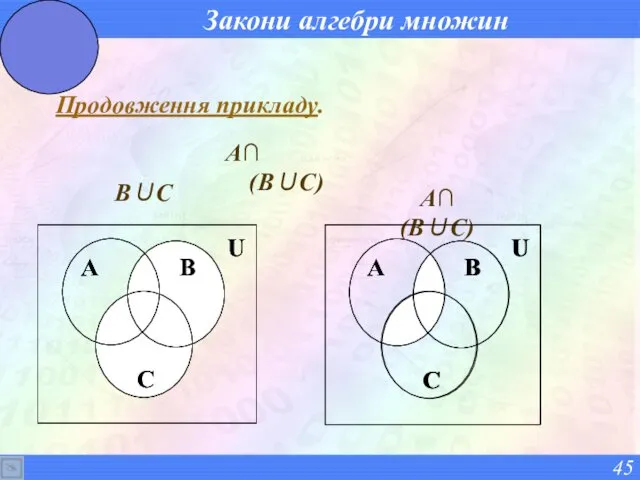
- 45. Закони алгебри множин Продовження прикладу. В∪С А∩ (В∪С) А∩ (В∪С)
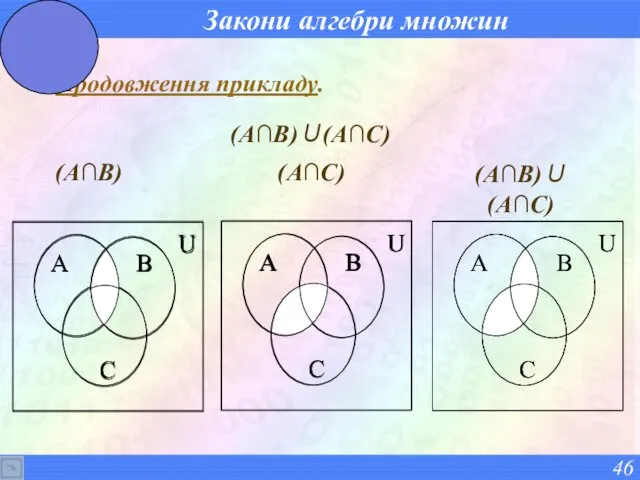
- 46. Закони алгебри множин Продовження прикладу. (А∩В) (А∩С) (А∩В)∪(А∩С) (А∩В)∪(А∩С)
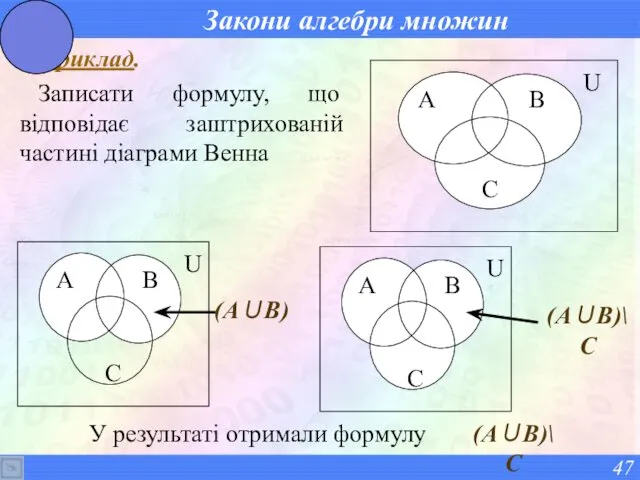
- 47. Закони алгебри множин Приклад. Записати формулу, що відповідає заштрихованій частині діаграми Венна (А∪В) У результаті отримали
- 48. Закони алгебри множин Приклад. Спростити вираз: Відповідь:
- 49. Взаємно-однозначна відповідність Взаємно-однозначною називається така відповідність між множинами A та B, при якій кожному елементу a∈A
- 50. Еквівалентні множини Множини A і B називаються еквівалентними (A~B), якщо між ними існує бієкція (принаймні одна).
- 51. Зліченні множини Множина A називається зліченною, якщо вона еквівалентна натуральному ряду N (A~N). За допомогою бієкції
- 52. Зліченні множини Множина парних натуральних чисел Nч={2,4,…,m,…}, всіх натуральних чисел N={1,2,…,n, …}, цілих чисел Z та
- 53. Нескінченні множини. Зліченні, континуальні множини Існують нескінченні зліченні множини, і їх потужність вважають більшою, ніж |N|.
- 55. Скачать презентацию













































 Создание персонального сайта учителя
Создание персонального сайта учителя Медицинские информационные системы классификация, цели, принципы использования, достоинства, недостатки, основные пути развития
Медицинские информационные системы классификация, цели, принципы использования, достоинства, недостатки, основные пути развития Человек и информация. Органы чувств
Человек и информация. Органы чувств Понятие программы. Лекция 1
Понятие программы. Лекция 1 Базы данных Системы управления базами данных
Базы данных Системы управления базами данных Коммутаторы в локальных сетях. Ethernet совместимые технологии
Коммутаторы в локальных сетях. Ethernet совместимые технологии Приложение в программе DELPHI в виде теста
Приложение в программе DELPHI в виде теста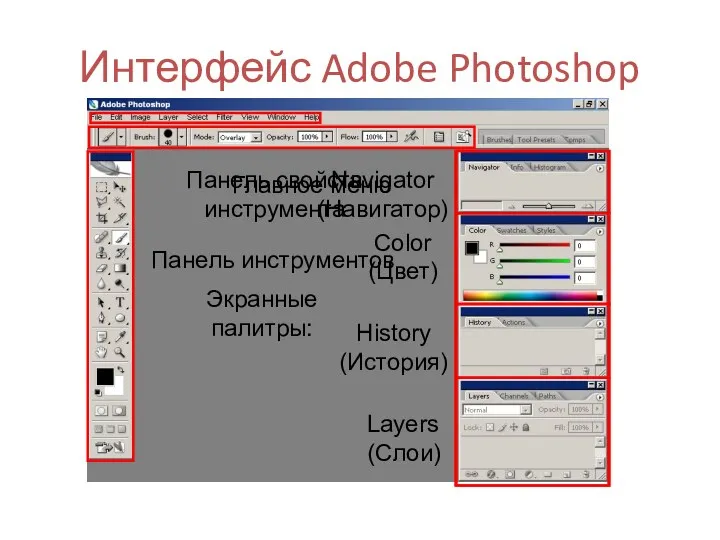 Интерфейс Adobe Photoshop
Интерфейс Adobe Photoshop Школьная библиотека: Копилочка. Инновационные формы профессионального взаимодействия
Школьная библиотека: Копилочка. Инновационные формы профессионального взаимодействия Електронна пошта
Електронна пошта Типы таблиц
Типы таблиц Администрирование информационных систем. Домены Windows, Active Directory
Администрирование информационных систем. Домены Windows, Active Directory Управление данными. Язык SQL. (Лекция 6)
Управление данными. Язык SQL. (Лекция 6) Компьютерлік графика
Компьютерлік графика The relational model
The relational model Введение в курс тестирования. (Занятие 1)
Введение в курс тестирования. (Занятие 1) Возможности программы КОМПАС 3D
Возможности программы КОМПАС 3D Правила безопасного поведения в интернете для детей и подростков
Правила безопасного поведения в интернете для детей и подростков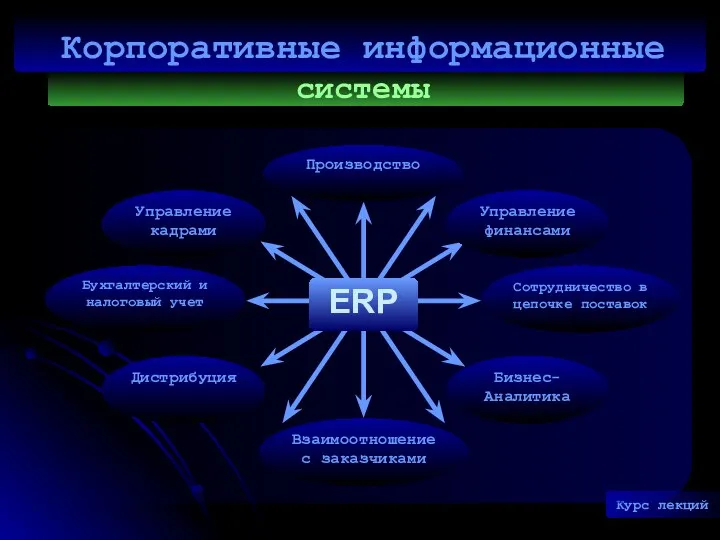 Корпоративные информационные системы. Информационные технологии и системы в менеджменте. Тема 1
Корпоративные информационные системы. Информационные технологии и системы в менеджменте. Тема 1 Кодування джерела неперервних повідомлень
Кодування джерела неперервних повідомлень Методы и средства защиты от несанкционированного доступа
Методы и средства защиты от несанкционированного доступа Компьютерная графика
Компьютерная графика Современные компьютерные технологии. (Modern Computer technologies)
Современные компьютерные технологии. (Modern Computer technologies) Компьютерный вирус (вымогатель)
Компьютерный вирус (вымогатель) Современные тенденции процесса цифровизации в Казахстане
Современные тенденции процесса цифровизации в Казахстане Современная журналистика. Блогинг. Занятие 2
Современная журналистика. Блогинг. Занятие 2 Персональный компьютер
Персональный компьютер Разработка программных модулей
Разработка программных модулей