Содержание
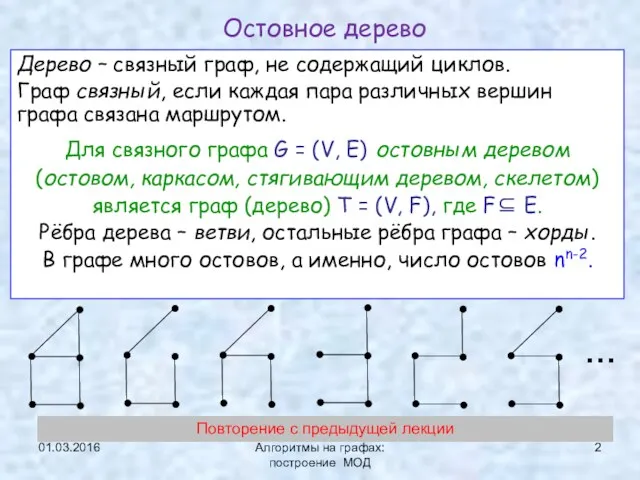
- 2. 01.03.2016 Алгоритмы на графах: построение МОД Дерево – связный граф, не содержащий циклов. Граф связный, если
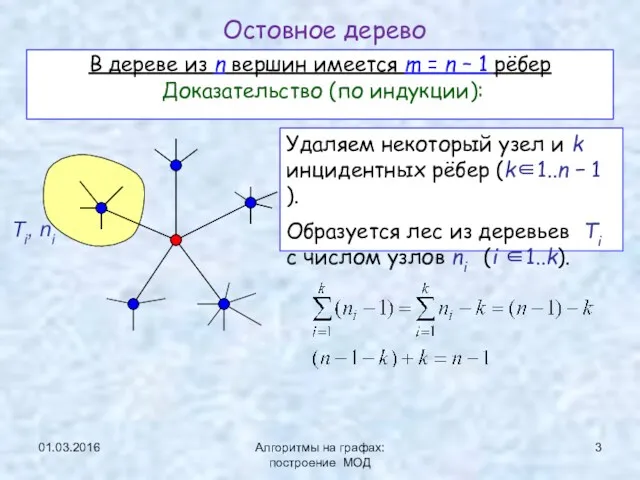
- 3. 01.03.2016 Алгоритмы на графах: построение МОД В дереве из n вершин имеется m = n –
- 4. 01.03.2016 Алгоритмы на графах: построение МОД Граф G = (V, E). Матрица весов W[v, u]. Пусть
- 5. 01.03.2016 Алгоритмы на графах: построение МОД Формулировка 1: Пусть веса всех рёбер различны. Тогда оптимальное остовное
- 6. 01.03.2016 Алгоритмы на графах: построение МОД Формулировка 2: Существует (найдётся) оптимальное остовное дерево графа, содержащее ребро
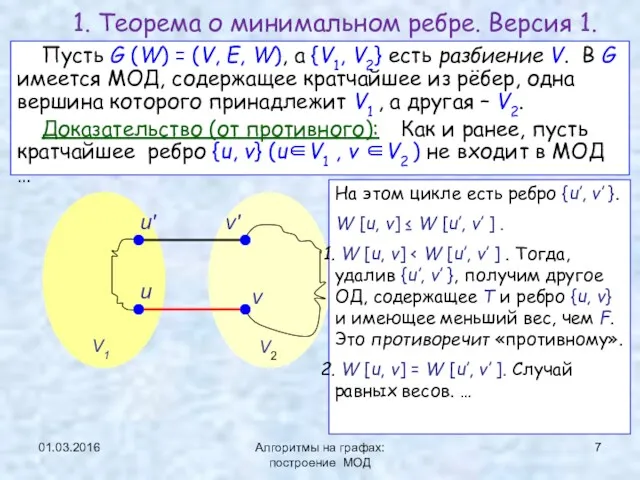
- 7. 01.03.2016 Алгоритмы на графах: построение МОД Пусть G (W) = (V, E, W), а {V1, V2}
- 8. 01.03.2016 Алгоритмы на графах: построение МОД 1. Теорема о минимальном ребре. Версия 2 Пусть {(V1, T1),
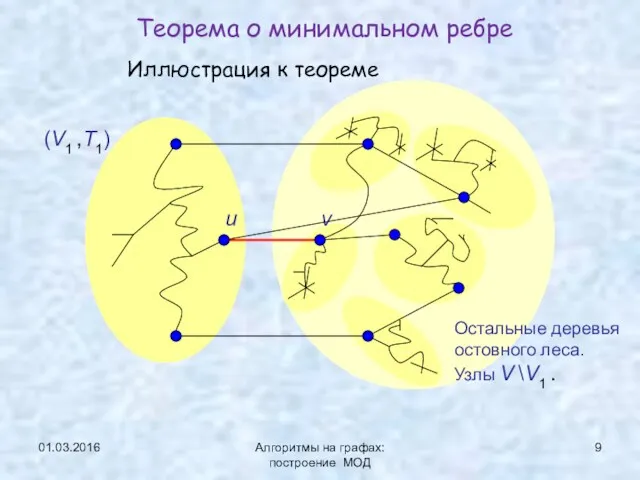
- 9. 01.03.2016 Алгоритмы на графах: построение МОД Иллюстрация к теореме Теорема о минимальном ребре (V1 ,Т1) v
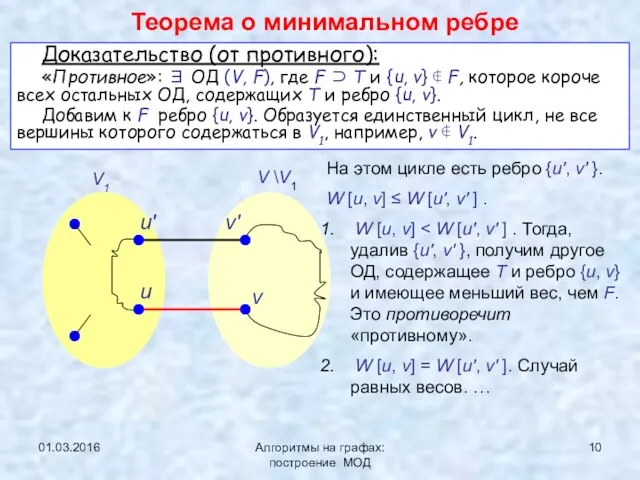
- 10. 01.03.2016 Алгоритмы на графах: построение МОД Доказательство (от противного): «Противное»: ∃ ОД (V, F), где F
- 11. 01.03.2016 Алгоритмы на графах: построение МОД Алгоритмы построения МОД Бoрувка (O. Bоruvka, 1926) Ярник (V. Jarnik,
- 12. 01.03.2016 Алгоритмы на графах: построение МОД «Краскал – Крускал» Материал из Википедии «Алгоритм Краскала — алгоритм
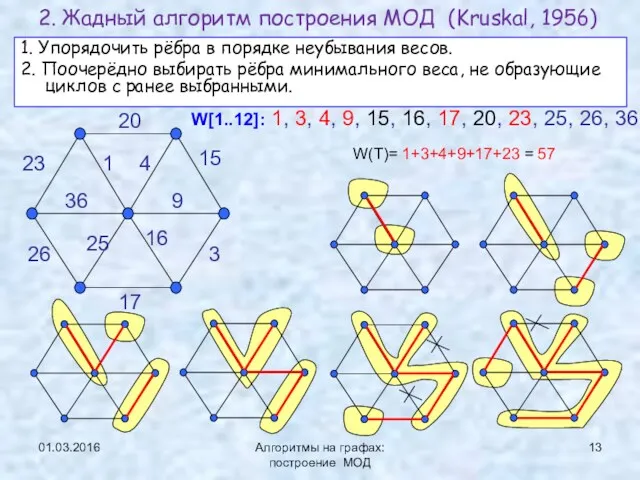
- 13. 01.03.2016 Алгоритмы на графах: построение МОД 1. Упорядочить рёбра в порядке неубывания весов. 2. Поочерёдно выбирать
- 14. 01.03.2016 Алгоритмы на графах: построение МОД Жадный алгоритм построения МОД (Kruskal, 1956) Vs - множество множеств
- 15. Жадный алгоритм построения МОД (Kruskal, 1956) // алгоритм МОД // Vs - множество деревьев остовного леса
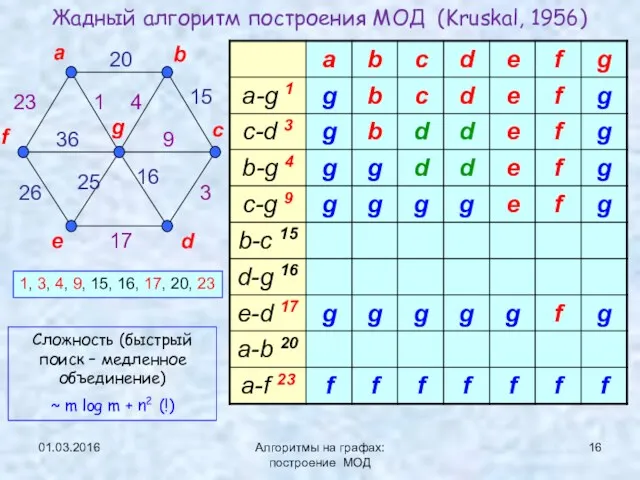
- 16. 01.03.2016 Алгоритмы на графах: построение МОД Жадный алгоритм построения МОД (Kruskal, 1956) a b c d
- 17. 01.03.2016 Алгоритмы на графах: построение МОД Корректность алгоритма (Теорема+индукция). Сложность алгоритма O(m log m) при соответствующей
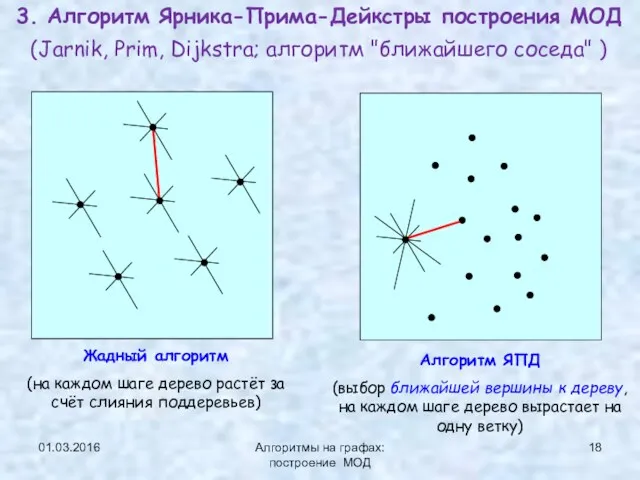
- 18. 01.03.2016 Алгоритмы на графах: построение МОД 3. Алгоритм Ярника-Прима-Дейкстры построения МОД (Jarnik, Prim, Dijkstra; алгоритм "ближайшего
- 19. 01.03.2016 Алгоритмы на графах: построение МОД Корректность алгоритма: из теоремы, при этом (V1, T1) – дерево,
- 20. 01.03.2016 Алгоритмы на графах: построение МОД Алгоритм Ярника-Прима-Дейкстры Используем специальную СД, которая облегчает выбор ближайшей вершины,
- 21. 01.03.2016 Алгоритмы на графах: построение МОД Вход : V - множество вершин графа G=(V,E), а d
- 22. 01.03.2016 Алгоритмы на графах: построение МОД //Детализация фрагмента ф1: min = +∞ ; for (∀ x
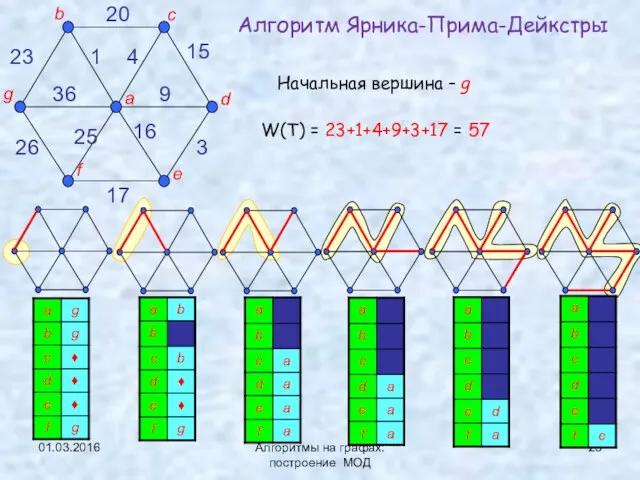
- 23. 01.03.2016 Алгоритмы на графах: построение МОД Алгоритм Ярника-Прима-Дейкстры Начальная вершина – g W(T) = 23+1+4+9+3+17 =
- 24. 01.03.2016 Алгоритмы на графах: построение МОД Худший случай: полный граф m = n(n − 1)/2. Алгоритм
- 25. 4. Нижняя граница задачи нахождения МОД (2) Можно рассуждать иначе (чуть менее формально). Во входной весовой
- 26. 01.03.2016 Алгоритмы на графах: построение МОД Пусть наряду с near[*] используется рабочий массив расстояний dist[x] =
- 27. 01.03.2016 Алгоритмы на графах: построение МОД Алгоритм Ярника-Прима-Дейкстры построения МОД Примеры выполнения. Варианты: Стандартный - для
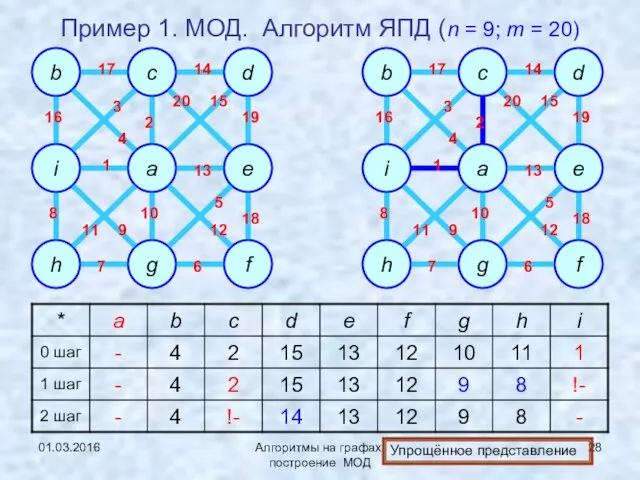
- 28. 01.03.2016 Алгоритмы на графах: построение МОД Пример 1. МОД. Алгоритм ЯПД (n = 9; m =
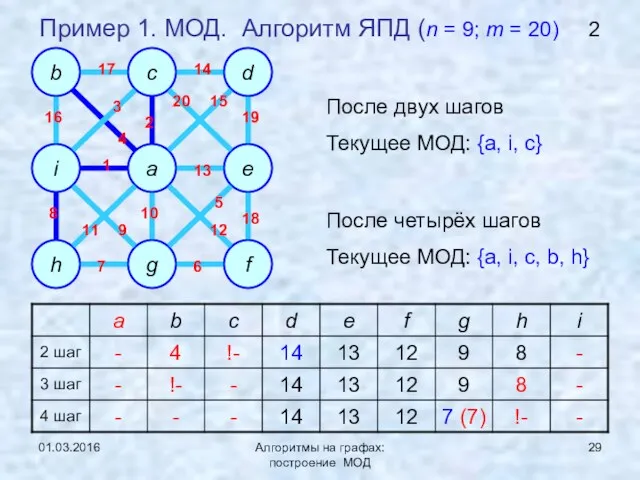
- 29. 01.03.2016 Алгоритмы на графах: построение МОД Пример 1. МОД. Алгоритм ЯПД (n = 9; m =
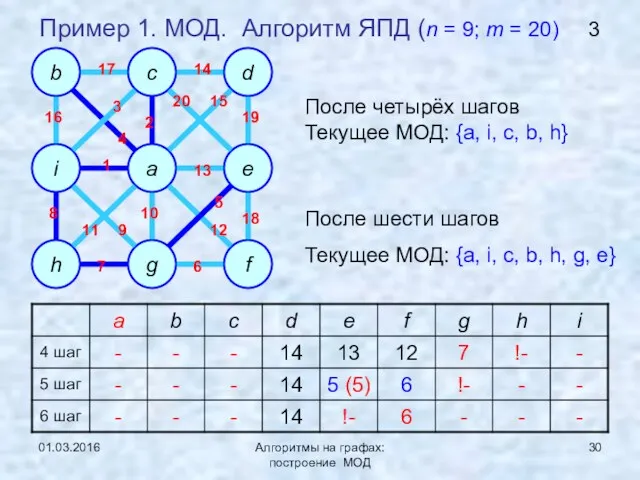
- 30. 01.03.2016 Алгоритмы на графах: построение МОД Пример 1. МОД. Алгоритм ЯПД (n = 9; m =
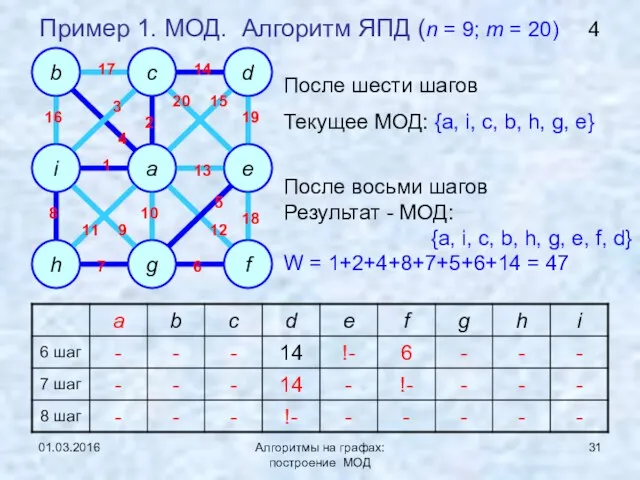
- 31. 01.03.2016 Алгоритмы на графах: построение МОД Пример 1. МОД. Алгоритм ЯПД (n = 9; m =
- 32. 01.03.2016 Алгоритмы на графах: построение МОД См. слайд 26 Пример выполнения алгоритма Ярника-Прима-Дейкстры (вариант для разрежённых
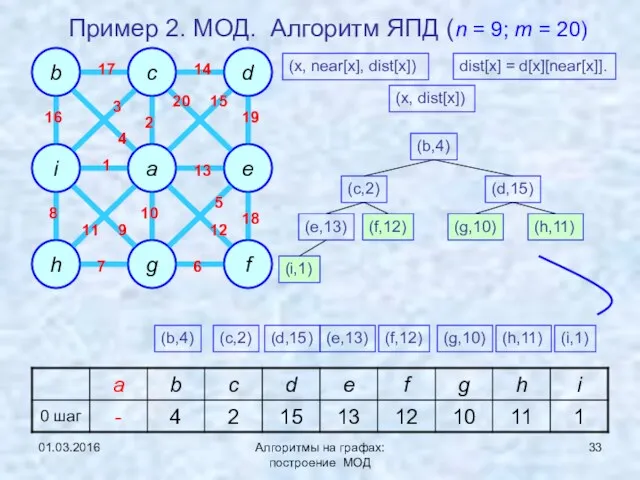
- 33. 01.03.2016 Алгоритмы на графах: построение МОД Пример 2. МОД. Алгоритм ЯПД (n = 9; m =
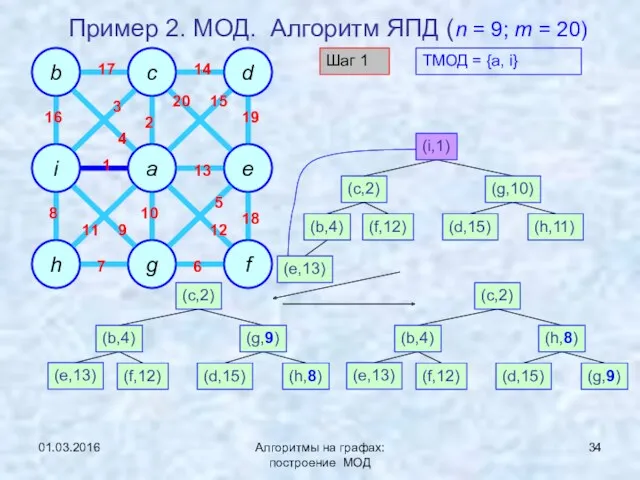
- 34. 01.03.2016 Алгоритмы на графах: построение МОД Пример 2. МОД. Алгоритм ЯПД (n = 9; m =
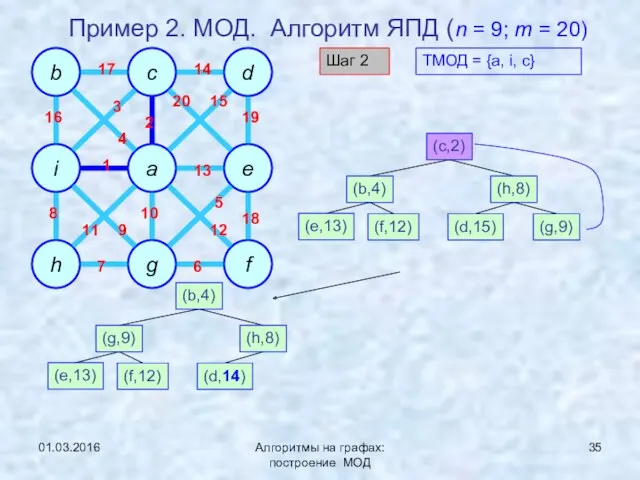
- 35. 01.03.2016 Алгоритмы на графах: построение МОД Пример 2. МОД. Алгоритм ЯПД (n = 9; m =
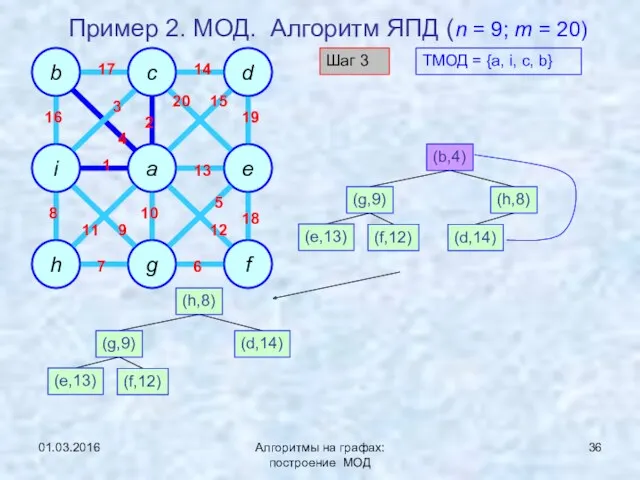
- 36. 01.03.2016 Алгоритмы на графах: построение МОД Пример 2. МОД. Алгоритм ЯПД (n = 9; m =
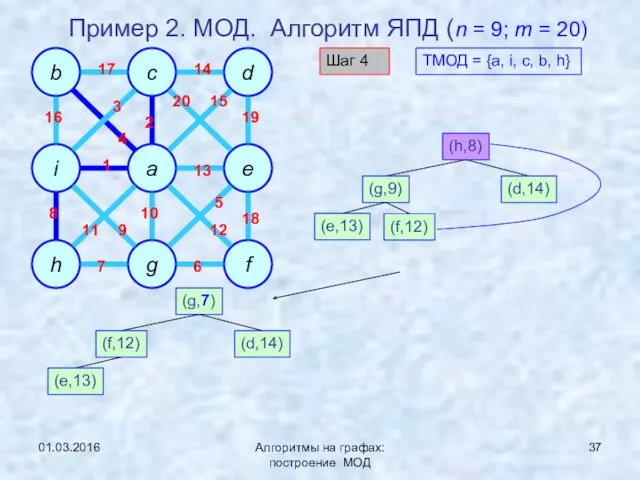
- 37. 01.03.2016 Алгоритмы на графах: построение МОД Пример 2. МОД. Алгоритм ЯПД (n = 9; m =
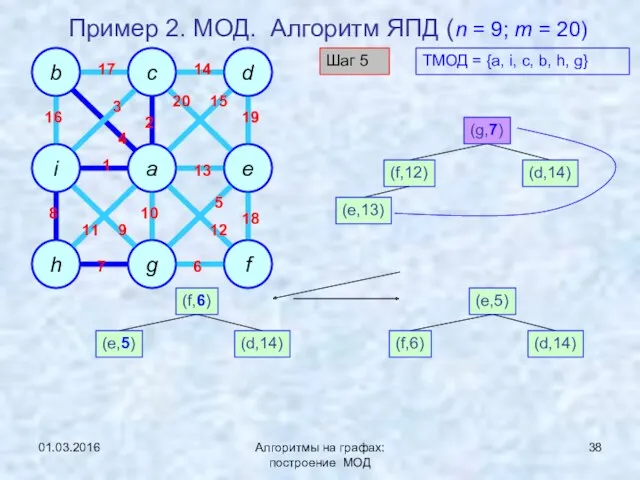
- 38. 01.03.2016 Алгоритмы на графах: построение МОД Пример 2. МОД. Алгоритм ЯПД (n = 9; m =
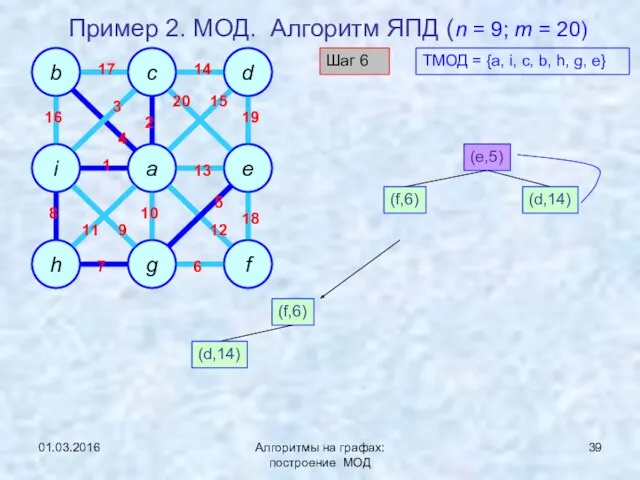
- 39. 01.03.2016 Алгоритмы на графах: построение МОД Пример 2. МОД. Алгоритм ЯПД (n = 9; m =
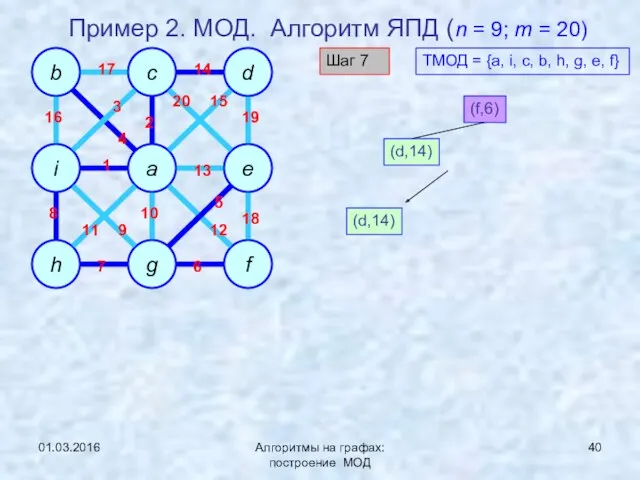
- 40. 01.03.2016 Алгоритмы на графах: построение МОД Пример 2. МОД. Алгоритм ЯПД (n = 9; m =
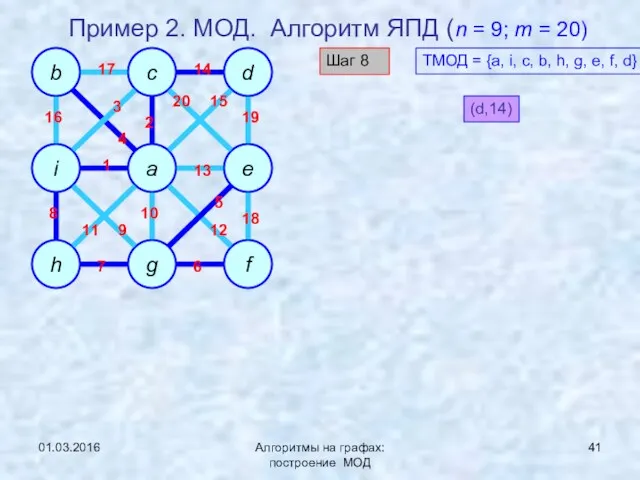
- 41. 01.03.2016 Алгоритмы на графах: построение МОД Пример 2. МОД. Алгоритм ЯПД (n = 9; m =
- 43. Скачать презентацию















![01.03.2016 Алгоритмы на графах: построение МОД Пусть наряду с near[*] используется рабочий массив](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/432197/slide-25.jpg)


 Работа с поисковой строкой
Работа с поисковой строкой Основы автоматизации технологических процессов
Основы автоматизации технологических процессов Оптимізація топології гетерогенної комп’ютерної мережі навчального закладу
Оптимізація топології гетерогенної комп’ютерної мережі навчального закладу Игра по информатике для учащихся 5 класса
Игра по информатике для учащихся 5 класса Горячие клавиши
Горячие клавиши Работа с файлами в Си-шарп
Работа с файлами в Си-шарп Виртуал бокс - Virtual Box
Виртуал бокс - Virtual Box Операционные системы
Операционные системы Инженерно-техническое, программно-аппаратное обеспечение и аудит информационной безопасности
Инженерно-техническое, программно-аппаратное обеспечение и аудит информационной безопасности Медиа-карта Региона. Радио СМИ
Медиа-карта Региона. Радио СМИ Рабочий стол. Управление мышью
Рабочий стол. Управление мышью Реляционные базы данных. Целостность данных. (Лекция 3)
Реляционные базы данных. Целостность данных. (Лекция 3) Складові комп’ютера. 2 клас
Складові комп’ютера. 2 клас Гугл плей маркет
Гугл плей маркет Функции проверки
Функции проверки Системы счисления. Перевод чисел из одной системы счисления в другую систему счисления
Системы счисления. Перевод чисел из одной системы счисления в другую систему счисления Апаратні та програмні засоби комп’ютерної графіки. (Тема 2)
Апаратні та програмні засоби комп’ютерної графіки. (Тема 2) Обработка информации
Обработка информации Навигатор дополнительного образования Архангельской области
Навигатор дополнительного образования Архангельской области Электронные таблицы Ехсel. (Лекция 3)
Электронные таблицы Ехсel. (Лекция 3) Представление о Power Point
Представление о Power Point Добавление рисунков, объектов, эффектов. Open Office.org 2.3 Impress
Добавление рисунков, объектов, эффектов. Open Office.org 2.3 Impress Презентация История языков программирования
Презентация История языков программирования История развития вычислительной техники
История развития вычислительной техники Электронное анонимное анкетирование студентов вуза
Электронное анонимное анкетирование студентов вуза Настройка анимации при создании презентаций в программе Power Point
Настройка анимации при создании презентаций в программе Power Point Управление процессами
Управление процессами План-конспект урока тема:Организация движения в среде формального исполнителя LogoWriter
План-конспект урока тема:Организация движения в среде формального исполнителя LogoWriter