Л.15 Метод Монте-Карло
Метрополіс, Розенблат, Теллер, 1953
Метод Метрополіса генерування нерівномірного розподілу ймовірності
являє собою частковий випадок процедури виборкипо значенню, в якій деякі моливі виборки відкидаються.
Одномірний випадок:
Потрібно згенерувати випадкові змінні (наприклад x) з довільною густиною ймовірності p(x). В методі Метрополіса моделюється “випадкове блукання” точок {xi}, розподіл яких після великої кількості кроків асимптотично прямує до розподілу ймовірності p(x). Випадкове блукання визначається заданням ймовірності переходу w(xi->xj) від одного значення xi до іншого xj для того, щоб розподіл точок x0 ,x1 , x2 ,... збігався до p(x).







 Функциональные возможности Microsoft Office
Функциональные возможности Microsoft Office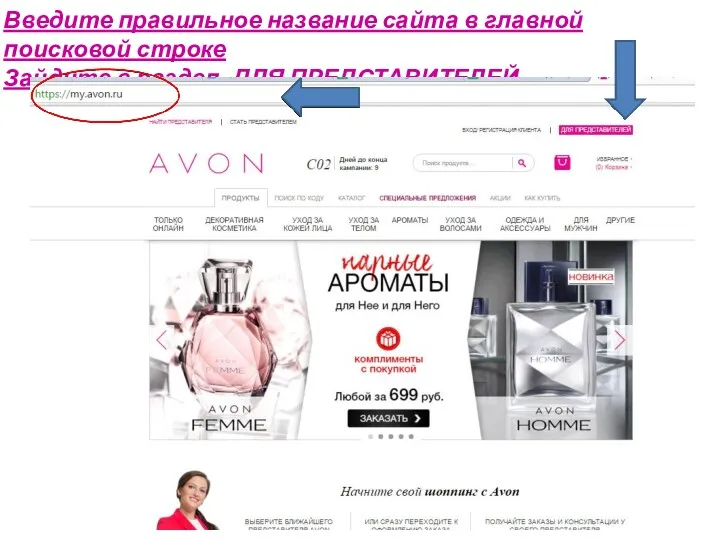 Как отправить заказ. Инструкция
Как отправить заказ. Инструкция Серия телеконференций Новое решение 1С:ERP
Серия телеконференций Новое решение 1С:ERP Маркировка товаров и штриховое кодирование
Маркировка товаров и штриховое кодирование Разработка программного средства Портфолио студента
Разработка программного средства Портфолио студента Цветоделение и подготовка макетов. Печать по текстилю
Цветоделение и подготовка макетов. Печать по текстилю Использование электронных образовательных ресурсов в обучении русскому языку и литературе
Использование электронных образовательных ресурсов в обучении русскому языку и литературе Конкурс на самый лучший репортаж. Приз от журнала Лестница
Конкурс на самый лучший репортаж. Приз от журнала Лестница Классификация графических работ
Классификация графических работ Pascal ABC. Графика
Pascal ABC. Графика Тестування програмних систем
Тестування програмних систем Преобразование логических выражений
Преобразование логических выражений История развития вычислительной техники
История развития вычислительной техники Брейн-ринг в информационном мире
Брейн-ринг в информационном мире Использование ИКТ на уроках физической культуры
Использование ИКТ на уроках физической культуры Внеклассное мероприятие по информатике
Внеклассное мероприятие по информатике Типы данных. Программа, написанная на языке Паскаль
Типы данных. Программа, написанная на языке Паскаль Этапы и инструментарий создания прогнозной концептуальной 3D гидрогеологической модели
Этапы и инструментарий создания прогнозной концептуальной 3D гидрогеологической модели Урок информатики в 5 классе с применением ИКТ Компьютер инструмент искусства.
Урок информатики в 5 классе с применением ИКТ Компьютер инструмент искусства. Внеклассное мероприятие. Путешествие с Инфознайкой
Внеклассное мероприятие. Путешествие с Инфознайкой Свойства информации. Измерение информации. Кодирование информации. Помехоустойчивое кодирование. Код хемминга. (Лекция 2)
Свойства информации. Измерение информации. Кодирование информации. Помехоустойчивое кодирование. Код хемминга. (Лекция 2) Основы трехмерного моделирования в САПР Компас - 3D. Создание заготовки чертежа
Основы трехмерного моделирования в САПР Компас - 3D. Создание заготовки чертежа Современная цифровая образовательная среда
Современная цифровая образовательная среда Основы программирования: ТЕМА 07. АЛГОРИТМЫ ОБРАБОТКИ ТАБЛИЦ.
Основы программирования: ТЕМА 07. АЛГОРИТМЫ ОБРАБОТКИ ТАБЛИЦ. Социальные сети для бизнеса
Социальные сети для бизнеса Linux Commands
Linux Commands Библиографическое описание книги
Библиографическое описание книги Урок по теме Работа со шрифтами. Форматирование текста. 8 класс.
Урок по теме Работа со шрифтами. Форматирование текста. 8 класс.