Содержание
- 2. Простые и составные числа Число n (n>1) называется простым, если имеет только два положительных делителя (1
- 3. Основные понятия* Решение задачи программируют так, чтобы с помощью программы решить любой возможный экземпляр задачи, который
- 4. Алгоритмы Вспомним, что такое «алгоритм». Под «алгоритмом» обычно понимают четко определенную последовательность действий, приводящую через конечное
- 5. Алгоритмы Основные свойства, присущие любому алгоритму: массовость — алгоритм предназначен для решения задачи с некоторым множеством
- 6. Алгоритмы Не для любой задачи существует алгоритм решения. Существуют алгоритмически неразрешимые задачи. Но даже если алгоритм
- 7. Алгоритмически неразрешимые задачи
- 8. Неразрешимость:
- 9. Проблема 2: Вычисление совершенных чисел Совершенные числа – это числа, которые равны сумме своих делителей, например:
- 10. Неразрешимость: Нет общего метода вычисления совершенных чисел, мы даже не знаем, множество совершенных чисел конечно или
- 11. Сложность алгоритма Сложность алгоритма – это количественная характеристика ресурсов, необходимых алгоритму для успешного решения поставленной задачи.
- 12. Модель вычислений RAM Random Access Machine Исполнение каждой "простой" операции (+, -, =, if, call) занимает
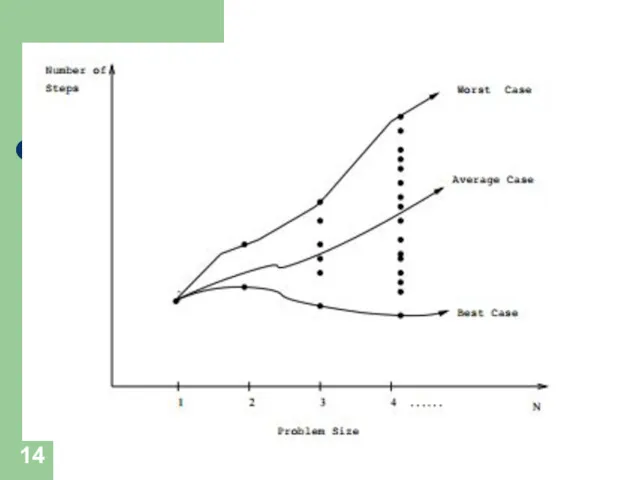
- 13. Анализ сложности наилучшего, наихудшего и среднего случаев ОХ: размер входа задачи (кол-во эл-тов и при сортировке
- 15. Сложность алгоритма -- В наихудшем случае -- функция, определяемая максимальным количеством шагов, требуемых для обработки любого
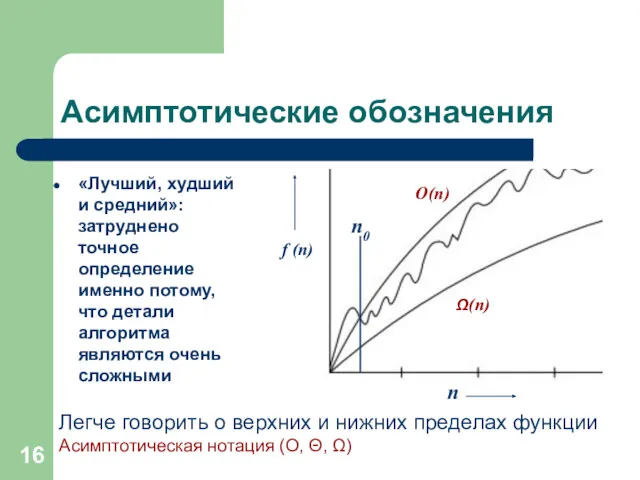
- 16. Асимптотические обозначения «Лучший, худший и средний»: затруднено точное определение именно потому, что детали алгоритма являются очень
- 17. Смысл асимптотических функций: g(n) = O(f(n)) означает, что C × f(n) является верхней границей функции g(n)
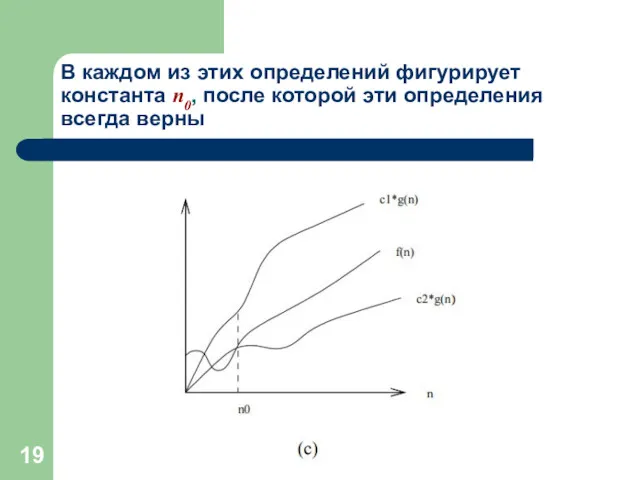
- 19. В каждом из этих определений фигурирует константа n0, после которой эти определения всегда верны
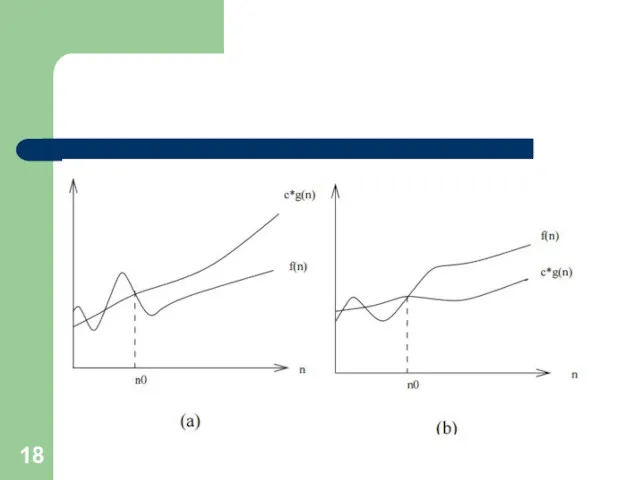
- 20. Формальные определения: f(n) = O(g(n)) означает, что функция f(n) ограничена сверху функцией c · g(n), т.
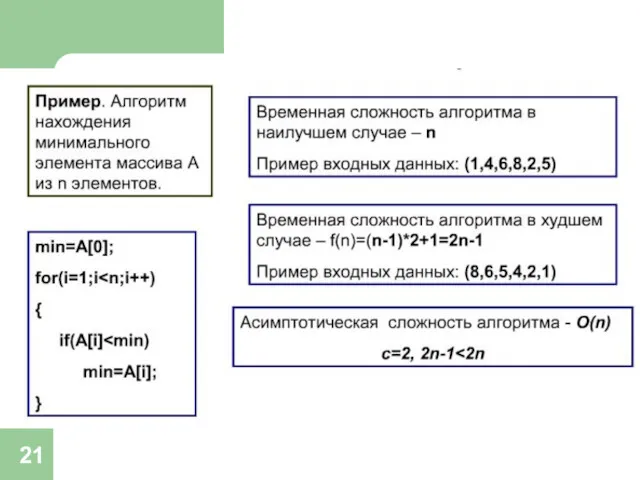
- 21. Пример
- 22. Примеры
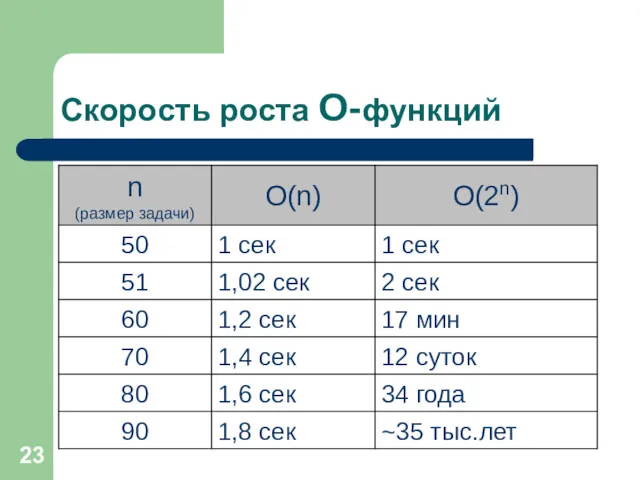
- 23. Скорость роста O-функций
- 24. Свойства асимптотических функций 1) Умножение на константу с>0 – не меняет асимптотических функций 2) При возрастании
- 25. Класс алгоритмов
- 26. ЗАПОМНИТЬ Оцените эффективность алгоритма сортировки методом выбора
- 27. 1) Расположите функции в возрастающем асимптотическом порядке:
- 28. Оценка сложности алгоритмов 1) Какое значение возвращает функция? Ответ должен быть в виде функции числа n.
- 29. Оценка сложности алгоритмов Сумма членов арифметической прогрессии 1-го порядка: 2 порядка: 3 порядка:
- 30. Решение задачи (1 вариант)
- 33. Оценка сложности алгоритмов Сортировка методом выбора: // счетчики //указатель min элемента
- 34. Домашнее задание:
- 36. Скачать презентацию























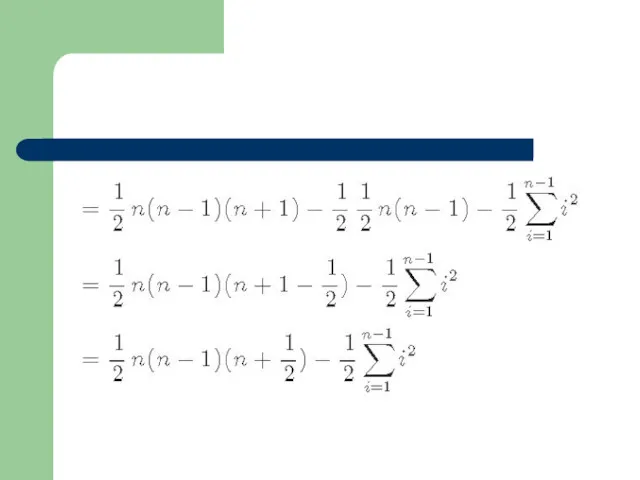



 Логические основы
Логические основы История развития вычислительной техники
История развития вычислительной техники Электронный билет на кинопоказ в районный дом культуры
Электронный билет на кинопоказ в районный дом культуры Знакомство с TrikStudio
Знакомство с TrikStudio Алгоритмы. Что такое алгоритм?
Алгоритмы. Что такое алгоритм? Виды БД
Виды БД Абстрактные классы
Абстрактные классы Компьютерные презентации
Компьютерные презентации Концептуалды үлгілеую. ER-диаграмма
Концептуалды үлгілеую. ER-диаграмма Файловая система. Операционные системы. Лекция 3
Файловая система. Операционные системы. Лекция 3 Звіт щодо результатів впровадження пілотного проекту Поліклініка без черг
Звіт щодо результатів впровадження пілотного проекту Поліклініка без черг Паспорт проекта Графическая новелла Эвелон 224
Паспорт проекта Графическая новелла Эвелон 224 Steps in Normalization
Steps in Normalization Разработка программного обеспечения на примере отечественного производителя Эльбрус
Разработка программного обеспечения на примере отечественного производителя Эльбрус Технология оцифровки архивных документов. Теория и практика
Технология оцифровки архивных документов. Теория и практика Электронное учебное пособие по теме Состав персонального компьютера
Электронное учебное пособие по теме Состав персонального компьютера CSS Grid Layout
CSS Grid Layout Поиск публикаций и показатели деятельности ученого в Web of Science
Поиск публикаций и показатели деятельности ученого в Web of Science Информационные системы в складской логистике. Лекция 5
Информационные системы в складской логистике. Лекция 5 Устройства ПК
Устройства ПК Технология NAT-Network Address Translation
Технология NAT-Network Address Translation Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно
Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно Кроссворд про школу (с клавиатурой)
Кроссворд про школу (с клавиатурой) Alcatel 1000 s12 digital switching system
Alcatel 1000 s12 digital switching system Линейные алгоритмы
Линейные алгоритмы Ваш безграничный бизнес в сети Интернет
Ваш безграничный бизнес в сети Интернет APM FEM Система прочностного анализа для КОМПАС-3D
APM FEM Система прочностного анализа для КОМПАС-3D Российская информатика
Российская информатика