Solving ultimate pit limit problem through graph closure (L-G algorithm) and the fundamental tree algorithm презентация

Contents
1. Introduction
2. Lerchs – Grossmann (Graph closure)
3. Fundamental Tree Algorithm
4. Assignment

Introduction
Two ojectives for open pit optimization
Design ultimate pit limits (Moving cone, LG, Net work flows …. )
Determining an optimal sequence of extracting the mineralized material from the ground (Short-term and Long-term production scheduling).
Lerchs, H., and Grossmann, I. F., 1965. Optimum Design of Open Pit Mines, Canad. Inst. Mining Bull. 58, pp. 47-54.
Salih Ramazan, The new Fundamental Tree Algorithm for production scheduling of open pit mines, European Journal of Operational Research 177 (2007) 1153–1166

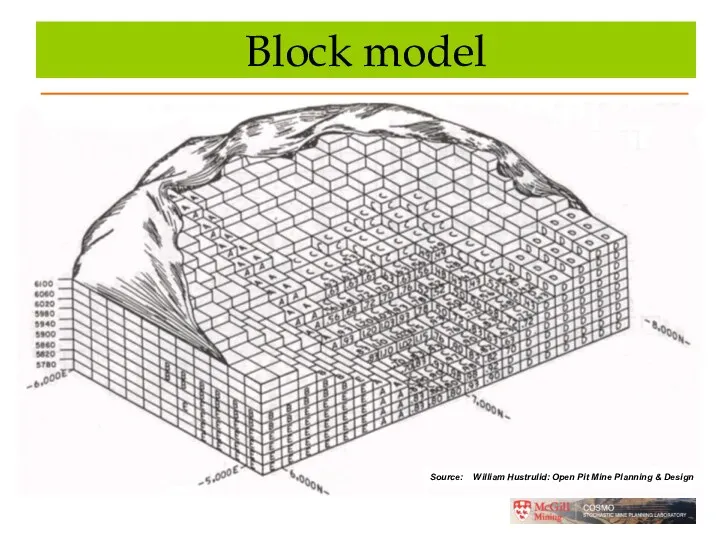
Block model
gdg
Source: William Hustrulid: Open Pit Mine Planning & Design

DEPOSIT REPRESENTATION OREBODY MODEL
A set of mining blocks of a given size with block value
BV: Economic Value of a mining block

DEPOSIT REPRESENTATION OREBODY MODEL
Geologic Model, Copper Grades (lb/ton)
Economic Model, Value per block ($/ton)

Ultimate Pit Limit Problems
Moving (Floating) Cone Algorithm
Dynamic Programming (LG)
Graph closure (Lerchs-Grossmann, Minimum Cut , Pseudo-flow Algorithm)

2. Graph closure (LG)
The optimal pit outline is the 3D pit outline which, if mined out, would give the maximum value
Must obey the required pit slope constraints
All the ore which at a given time can be mined at a profit will be mined
Nothing can be added to or taken away from the optimal outline which will increase the value without breaking the slope constraints

Lerchs-Grossman Algorithm
Mathematical search technique which works from just two sources of information:
1. Economic or value block model:
Set of regular rectangular blocks which completely fill the space under consideration for mining
2. A list of relationships between these blocks:
These relationships are known as `arcs'

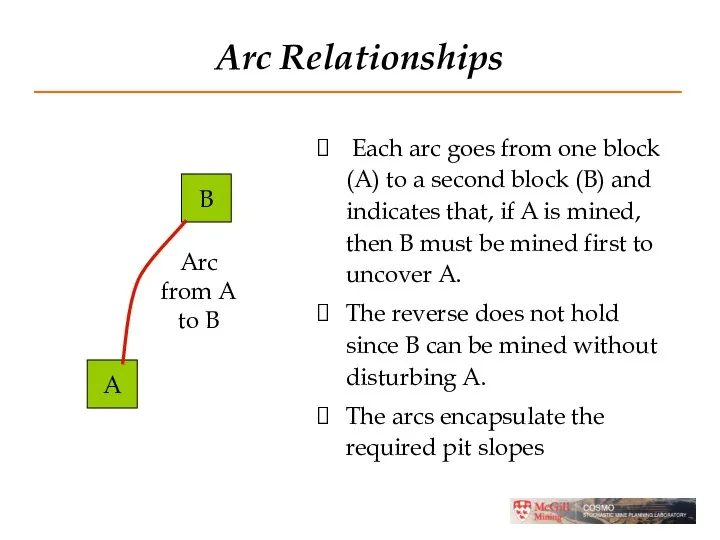
Arc Relationships
Each arc goes from one block (A) to a second block (B) and indicates that, if A is mined, then B must be mined first to uncover A.
The reverse does not hold since B can be mined without disturbing A.
The arcs encapsulate the required pit slopes
A
B

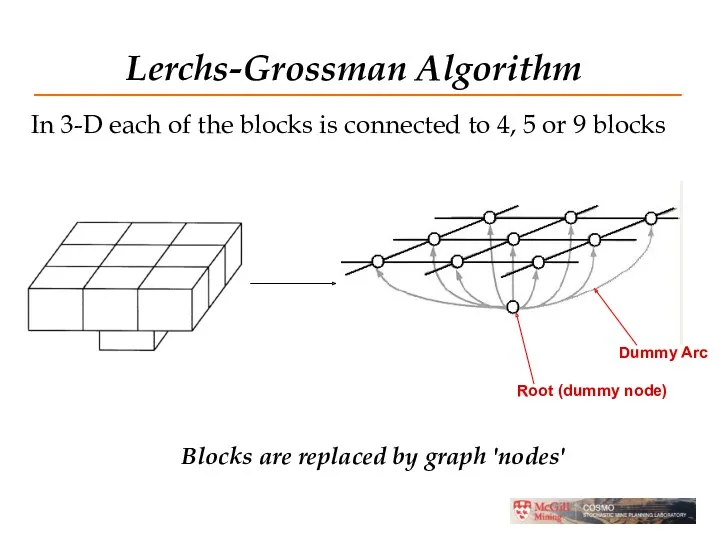
Lerchs-Grossman Algorithm
In 3-D each of the blocks is connected to 4, 5 or 9 blocks
Blocks are replaced by graph 'nodes'

DEFINITIONS
Directed graph G(X, A) is defined by a set of nodes X and a set of arcs A. The LG algorithm finds the maximum closure in the graph G (X, A).
X={x1,x2,….,xn} is called the vertices of G
A is the sets of arcs of G
A closure of G is defined as a set of vertices such that if
Graph representation of the orebody model and a closure.

BASIC TERMINOLOGY
Vertex, xi is the value of block i.
Arc, aij=(xi,xj), an arrow drawn from xi to xj.
Positive arc: an arc starting at an ore vertex towards and overlying waste vertex.
Negative arc: an arc from waste vertex to underlying ore vertex.
The vertex that an arc starts is predecessor and the one that the arc ends is successor

Root is the vertex without predecessor
A closure is any surface satisfying the slope constraints
An arc which is going away from the root is p-arc(+).
An arc which is going towards the root is m-arc (-).
The mass is the value of all the nodes a p-arc is supporting (going towards), and the value of all the nodes an m-arc is supported by, or leaving behind.
A p-arc is strong if it supports positive mass (ps), weak otherwise (pw).
BASIC TERMINOLOGY

An m-arc is weak if it is supported by positive mass (mw), strong otherwise (ms).
A path is a subgraph of G consisting of a sequence of nodes and arcs satisfying the property that the terminal node of an arc is the source node for the succeeding arc.
A chain is a sequence of edges in which each edge has one node in common with the succeeding edge.
A cycle is a chain in which the initial & final nodes coincide
BASIC TERMINOLOGY

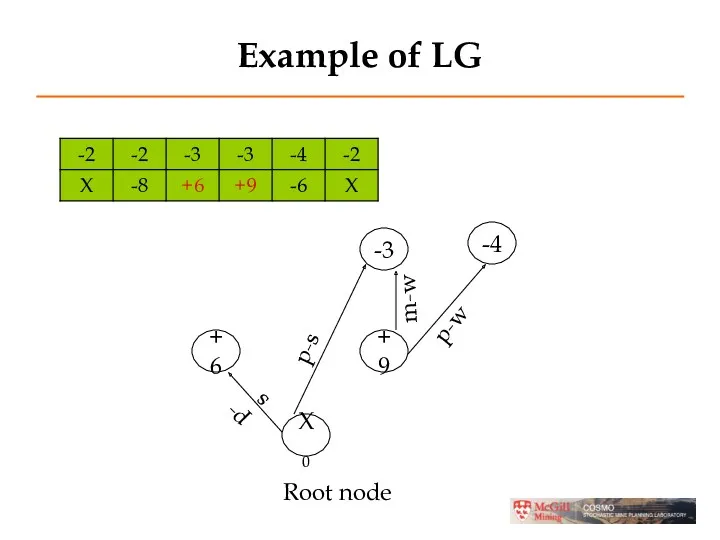
Example of LG
-3
-4
+6
+9
X0
p-s
m-w
p-w
p-s
Root node

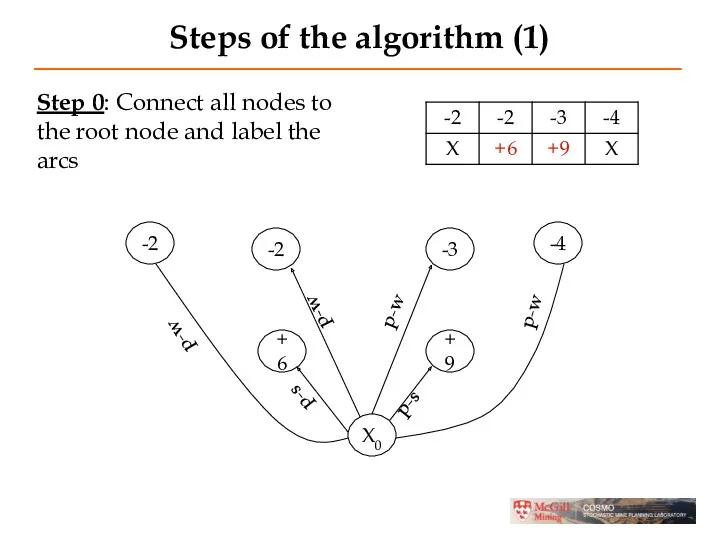
Steps of the algorithm (1)
-2
-2
-3
-4
+6
+9
X0
Step 0: Connect all nodes to the root node and label the arcs
p-w
p-w
p-w
p-w
p-s
p-s

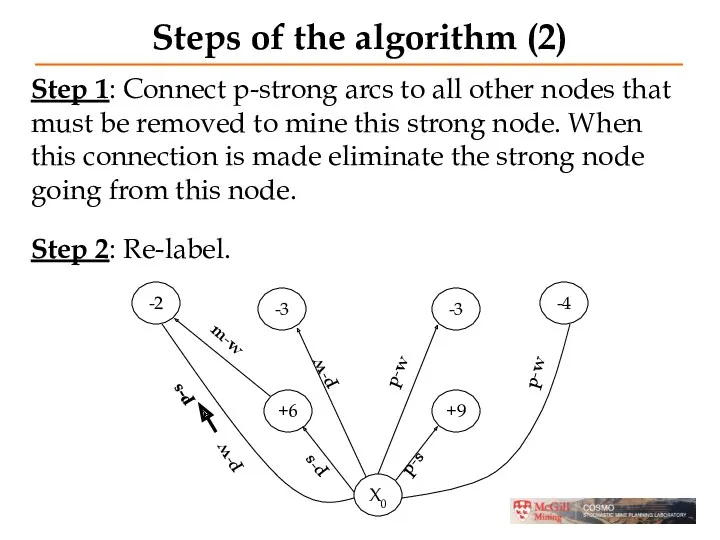
Steps of the algorithm (2)
-2
-3
-3
-4
+6
+9
X0
Step 1: Connect p-strong arcs to all other nodes that must be removed to mine this strong node. When this connection is made eliminate the strong node going from this node.
p-w
p-w
p-s
p-w
p-s
p-s
p-w
Step 2: Re-label.
m-w

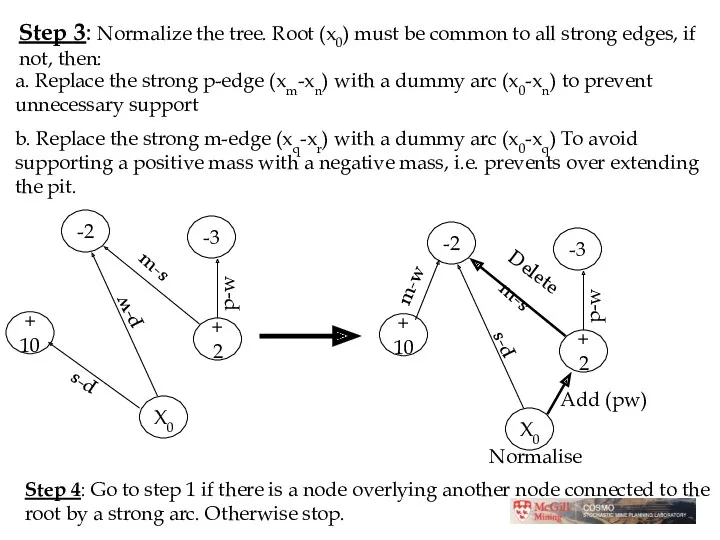
Step 3: Normalize the tree. Root (x0) must be common to all strong edges, if not, then:
a. Replace the strong p-edge (xm-xn) with a dummy arc (x0-xn) to prevent unnecessary support
b. Replace the strong m-edge (xq-xr) with a dummy arc (x0-xq) To avoid supporting a positive mass with a negative mass, i.e. prevents over extending the pit.
Step 4: Go to step 1 if there is a node overlying another node connected to the root by a strong arc. Otherwise stop.

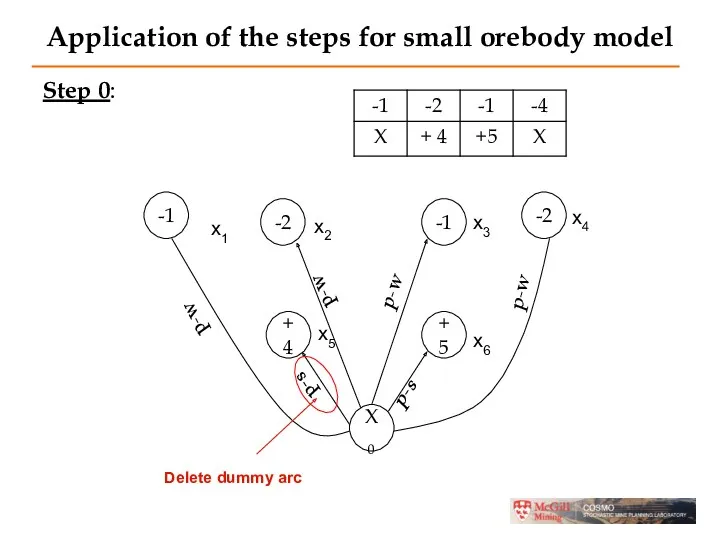
Application of the steps for small orebody model
Step 0:

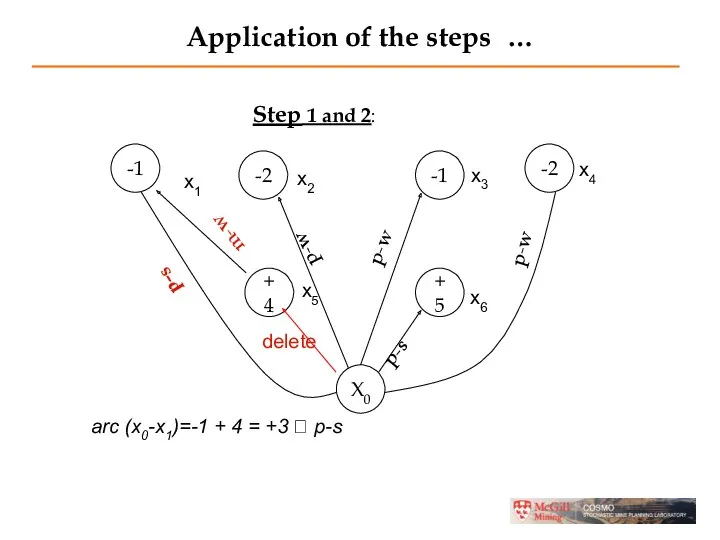
Application of the steps …
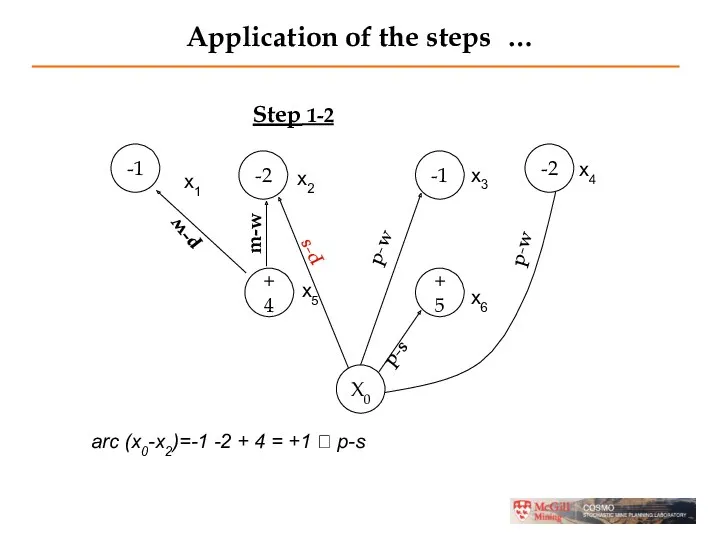
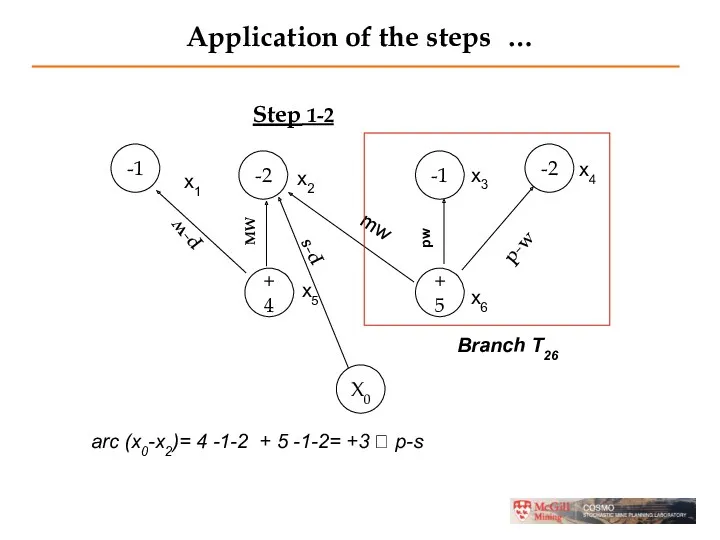
Step 1 and 2:

Application of the steps …
Step 1-2
-1
-2
-1
-2
+4
+5
X0
p-w
p-w
p-s
p-s
x2
x1
x3
x4
x5
x6
p-w
arc (x0-x2)=-1 -2 + 4 = +1 ? p-s
m-w

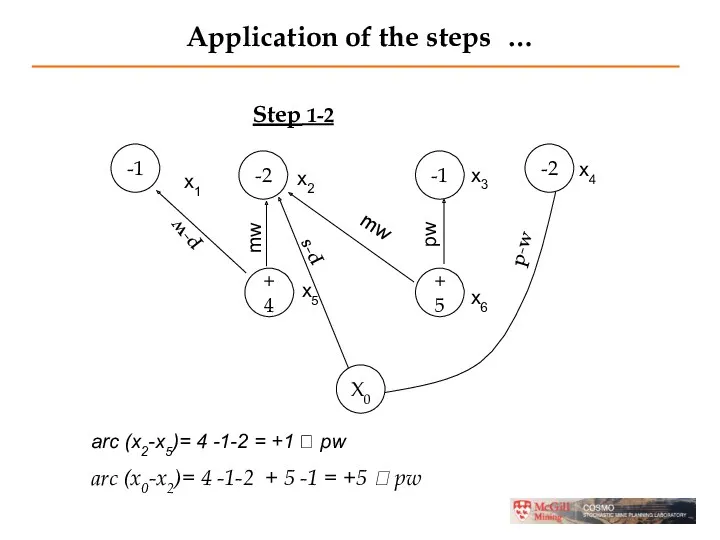
Application of the steps …
Step 1-2
-1
-2
-1
-2
+4
+5
X0
mw
p-w
p-s
x2
x1
x3
x4
x5
x6
p-w
arc (x2-x5)= 4 -1-2 = +1 ? pw
arc (x0-x2)= 4 -1-2 + 5 -1 = +5 ? pw
mw
pw

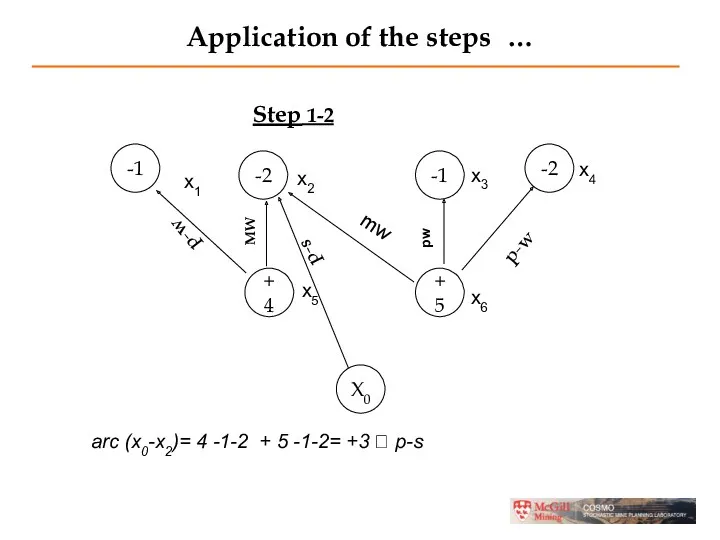
Application of the steps …
Step 1-2
arc (x0-x2)= 4 -1-2 + 5 -1-2= +3 ? p-s

Application of the steps …
Step 1-2
-1
-2
-1
-2
+4
+5
X0
mw
p-w
p-s
x2
x1
x3
x4
x5
x6
p-w
arc (x0-x2)= 4 -1-2 + 5 -1-2= +3 ? p-s
MW
pw
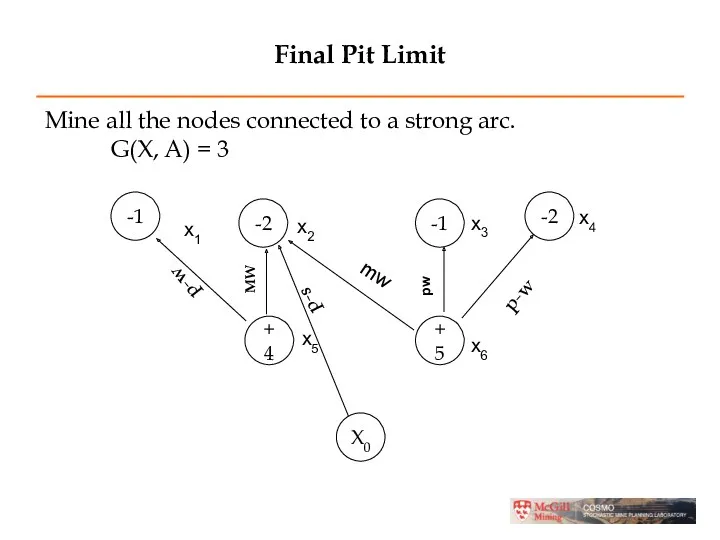
Branch T26

Final Pit Limit
Mine all the nodes connected to a strong arc.
G(X, A) = 3

Optimal Pit
The L-G algorithm will flag each block as being inside or outside the optimal pit outline
In the 3D algorithm, the optimal pit will be the pit with the highest net value
Revenue can be calculated from ore tonnages, grades, recoveries and product price.
Price is often the biggest unknown but, in order to design a pit, you must assume some price

Varying Slope Angles
It is possible to have different slope angles in different areas of the pit (different levels or different X, Y coordinates)
Results in an irregular pit wall (complete blocks being removed)
Bulges in the pit can lead to geotechnical concerns
Must be corrected before the pit is complete

3. Fundamental Tree Algorithm
Long-term production scheduling consists of determining an optimal sequence of extracting the mineralized material from the ground annualy.
MIP models are used to solve the problem for an open pit mine.
Assume that ultimate pit and pushbacks are given already.
Even optimizing the production schedule on a pushback using MIP can be too complex (too many blocks).

The Approach
To simplify the MIP we would like to decrease the number of blocks in our model so that the MIP model can be solved efficiently.
This is done by combining blocks that should be mined together as just one block.
We call the combined block a fundamental tree.

The Approach
A Fundamental Tree is defined as a combination of blocks such that:
The blocks can be profitably mined.
The blocks obey the slope constraints.
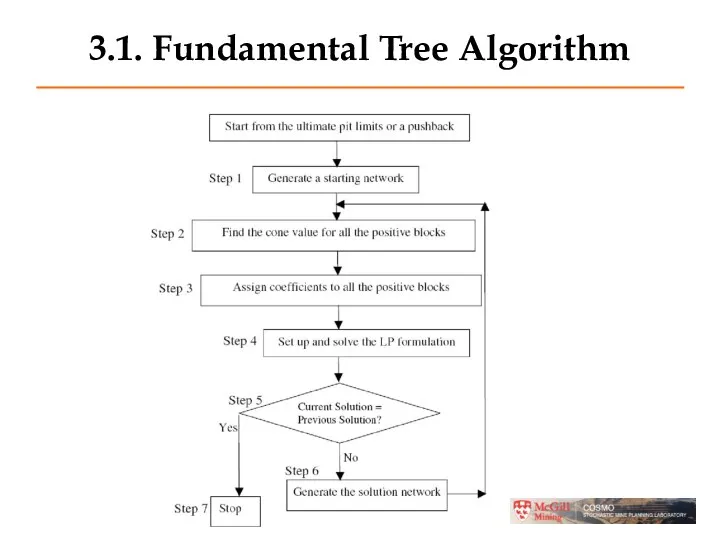
There is no proper subset of the chosen blocks that meets 1 and 2.

3.1. Fundamental Tree Algorithm

Step 1 - Generate a Starting Network
Given a our pushback block model represent blocks by nodes of a graph.
Arcs go from positive blocks to overlying negative blocks that must be removed before based on slope constraints.
We will use a network flow to find the fundamental trees.
To construct a network flow, we add a source node s and a sink node t.

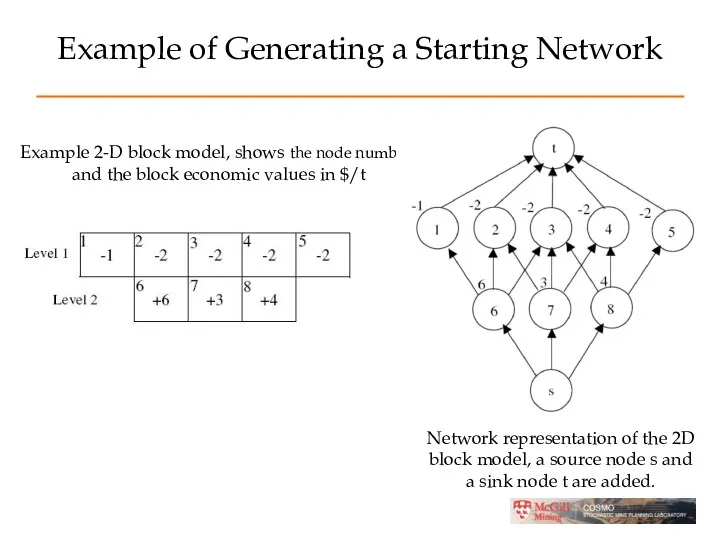
Example of Generating a Starting Network
Example 2-D block model, shows the node numbers and the block economic values in $/t
Network representation of the 2D block model, a source node s and a sink node t are added.

Step 2 - Find the Cone Value
The "cone" value of a block (CVi) is the sum of the block values of itself and all overlying blocks
We calculate the cone value of all positive nodes in our pushback (or pit), CVi
Example of step 2
CV6 = V6+V1+V2+V3
=+6 — 1 — 2 — 2 = +1
CV7 = —3,
CV8 = —2

Step 3 – Assign cofficients to the Positive Nodes
Each positive node will be assigned a cofficient, Ci which denotes the rank of node i.
Assign Ci to the nodes by ordering mining level firstly, then by cone value.
The maximum value on the top most level will be given size 1 for the highest cone, and the second highest cone value is 2 …
With tie condition, Cis are choosen randomly

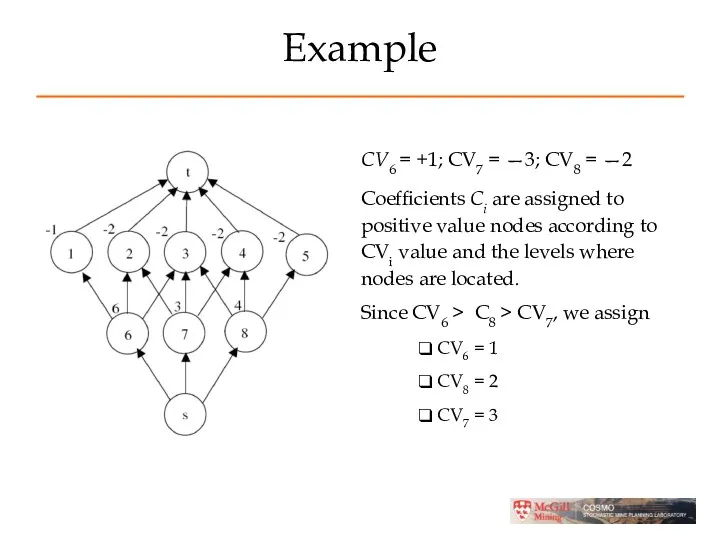
Example
CV6 = +1; CV7 = —3; CV8 = —2
Coefficients Ci are assigned to positive value nodes according to CVi value and the levels where nodes are located.
Since CV6 > C8 > CV7, we assign
CV6 = 1
CV8 = 2
CV7 = 3

Step 4 - Set up the LP
Set up a Linear Program to find the first iteration of Fundamental Trees.
The LP model can be solved using a commercially availble software such as CPLEX

Step 5 - Check if we are done
If the number of Fundamental Trees found is the same as the number of trees obtained from previous solution, go to Step 7.
Otherwise, go to Step 6 to reformulate the problem as a network flow and repeat. We do this by deleting arc with no flow from our network and resolving the new LP (go back Step 2).

3.2. Formulating the Linear Program
* The objective function:
Ci is the coefficient for node (block) i,
fi, j is the flow from block i to block j.
* The Flow Constraints:
fs, i < Vi ∀i where Vi > 0.
fj, t = -Vj +ξ

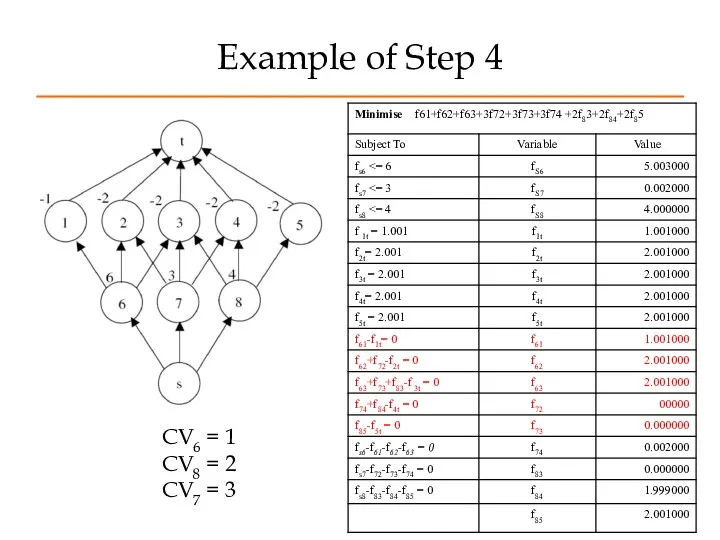
Example of Step 4

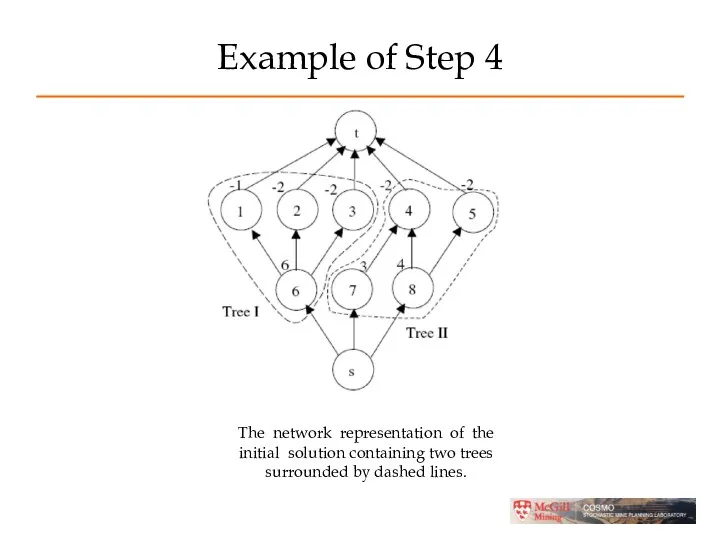
Example of Step 4
The network representation of the initial solution containing two trees surrounded by dashed lines.

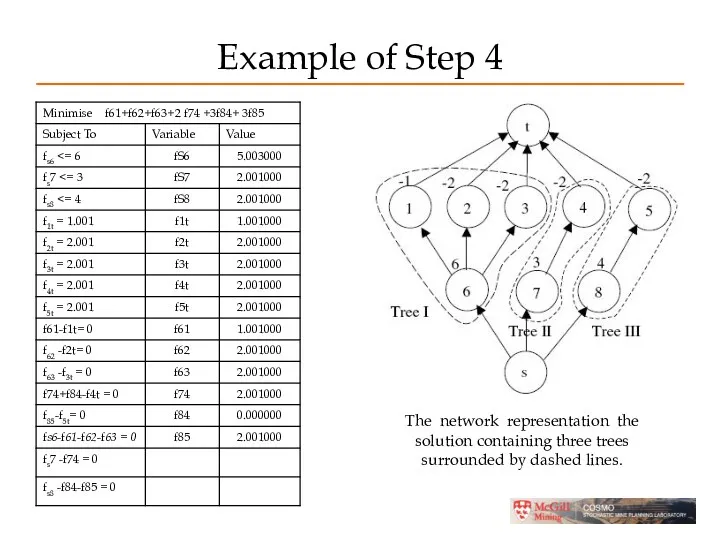
Example of Step 4
The network representation the solution containing three trees surrounded by dashed lines.

3.3. Properties of the fundamental trees
Property 1 - All fundamental trees have positive value is satisfied since:
and
Therefore,
The sum of all positive value nodes in a tree is greater than the sum of negative value nodes.

Property 2 of the fundamental trees
All fundamental trees obey the slope constraints if they are removed one at a time respecting the sequencing between them.
All overlying negative nodes must be supported by positive nodes by the LP constraints.

Property 3 of the fundamental trees
A tree found by FTcannot contain a subset of a fundamental tree that also can be a fundamental tree.
Base on the objective function,
Where i nodes are positive and j nodes are negative, if a smaller fundamental tree existed then our LP would have found it.

3.4. Optimization of annual production scheduling using fundamental trees
The optimization model is maximization of the NPV, or discounted economic value, to be generated from the mining operation
For scheduling N Fundamental Trees over Y years, the objective function can be expressed as:

using fundamental trees
Where:
DEVpi discounted economic value to be feberated from mining and processing all the ore tons in year, p from FTi, DEVpi = DEV0i*DFp (DFp = 1/(1.0 + d)p
DWCip discounted average cost of mining one ton waste from FTi in year p, DWCip = DWCi0*DFp
Wip is a linear variable representing the tons of the waste to be mined at period p from fundamental tree i
Oip is a binary variable, equal to 1 if the ore ton in FTi is scheduling for period p, 0 otherwise.

Subject to: ❶. Slope constraints:
If j is the index for the fundamental trees that have to be removed before being able to remove tree i in a period p:
If Ni is the number of overlying FTs for FT i:

❷. Sequencing of mining ore and waste
If mining the ore tonnages from a given FT, all the waste tonnages must be mined out in that FT.
Where:
- TWi is the total tons of waste material within tree i

❸. Grade blending constraints
Upper bound constraints: The average grade of the material sent to the mill has to be less than or equal to a certain grade value, Gmax, for each period, p
Lower bound constraints: The average grade of the material sent to the mill has to be greater than or equal to a certain value, Gmin, for each period, p
Where Gi is the average grade of FTi
TOi is the ore tonnage in FTi

❹. Processing capacity constraints
Upper bound: The total tonnage of ore processed cannot be more than the processing capacity (PCmax) in any period, p
Lower bound: The total tonnage of ore processed cannot be less than a certain amount (PCmin) in any period, p

❻. The limit on the stripping ratio in each period
Where
SRmax is the maximum stripping ratio allowed during any year
❺. Reserve constraints

❼. Mining capacity
The total amount of material mined during a year cannot be more than the total available equipment capacity (MCap) for each period, p
Where: Wip is the tonnage of waste material in FTi
❽ In some mining operation, the total tonnage of waste to be stripped out in a previod is not exceed a waste stripping amount (WCmax). For n-FTs and a given period, p,

3.5. Case Study: MIP Scheduling Formulation
One of the case studies is performed on a large copper mine in Southern Peru containing 1 million blocks
MIP formulations for mine scheduling treating fundamental trees as single blocks.
This algorithm reduced the number of blocks from 38457 to 5512 fundamental trees.
Therefore, large open pit production scheduling can be optimized by MIP modelling for any objective such as maximizing NPV of a given mine project, or to solve hard ore quality and grade blending problems

ASSIGNMENT 8
Consider the above 2D orebody model:
1. Show steps to determine the ultimate pit limits using:
a) Cone mining algorithm (if known)
b) LG algorithm (Dynamic Programming) (if known)
c) LG algorithm (Graph closure)
Describe the differences between the algorithms.
2. Write codes in C++ to solve the above problem using Graph closure (LG)