Содержание
- 2. ECE C03 Lecture 3 Outline CAD Tools for 2-level minimization Quine-McCluskey Method ESPRESSO Algorithm READING: Katz
- 3. ECE C03 Lecture 3 Two-Level Simplification Approaches Algebraic Simplification: not an algorithm/systematic procedure how do you
- 4. ECE C03 Lecture 3 Review of Karnaugh Map Method Algorithm: Minimum Sum of Products Expression from
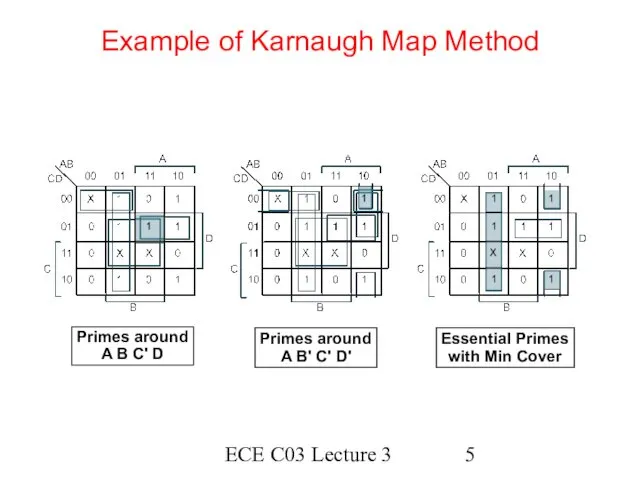
- 5. ECE C03 Lecture 3 Example of Karnaugh Map Method Primes around A B' C' D' Primes
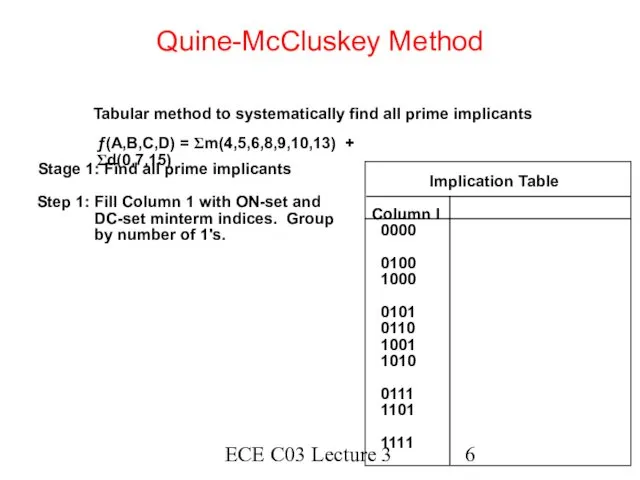
- 6. ECE C03 Lecture 3 Quine-McCluskey Method Tabular method to systematically find all prime implicants Implication Table
- 7. ECE C03 Lecture 3 Quine-McCluskey Method Tabular method to systematically find all prime implicants Implication Table
- 8. ECE C03 Lecture 3 Quine Mcluskey Method Tabular method to systematically find all prime implicants Implication
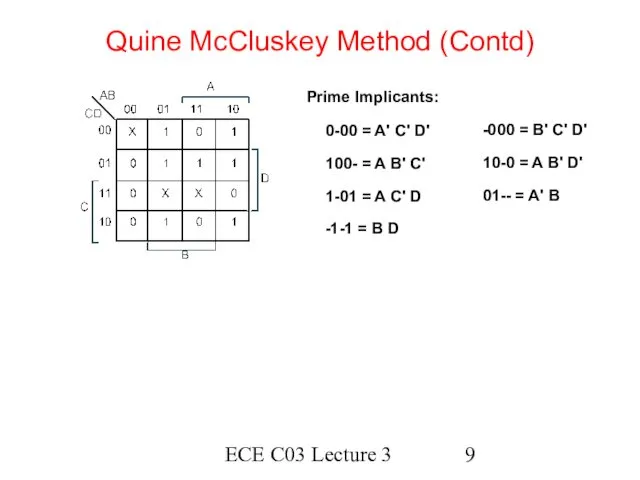
- 9. ECE C03 Lecture 3 Quine McCluskey Method (Contd) Prime Implicants: 0-00 = A' C' D' 100-
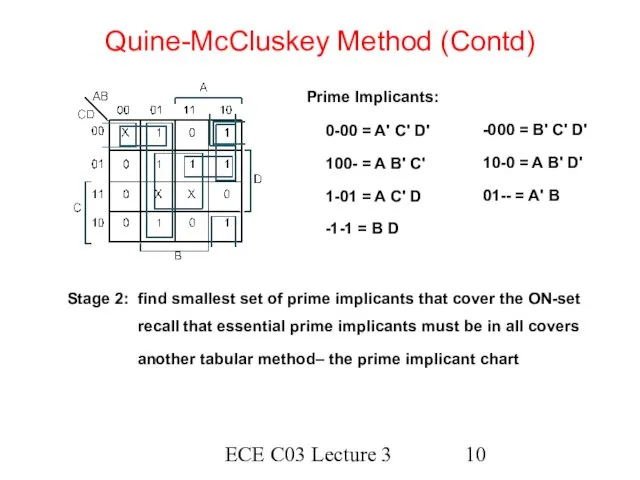
- 10. ECE C03 Lecture 3 Quine-McCluskey Method (Contd) Prime Implicants: 0-00 = A' C' D' 100- =
- 11. ECE C03 Lecture 3 Finding the Minimum Cover We have so far found all the prime
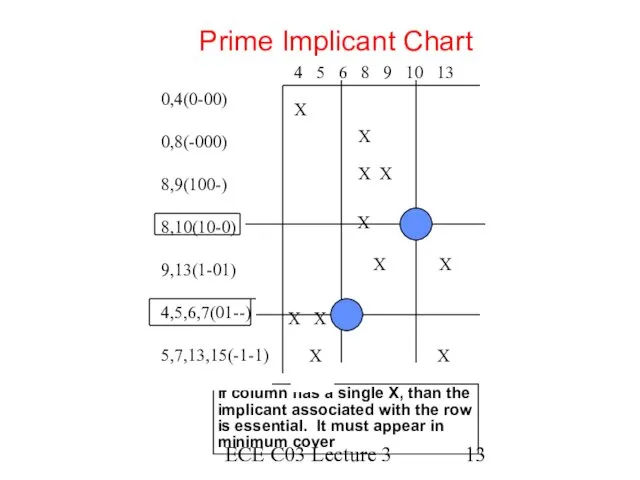
- 12. ECE C03 Lecture 3 Prime Implicant Chart rows = prime implicants columns = ON-set elements place
- 13. ECE C03 Lecture 3 Prime Implicant Chart If column has a single X, than the implicant
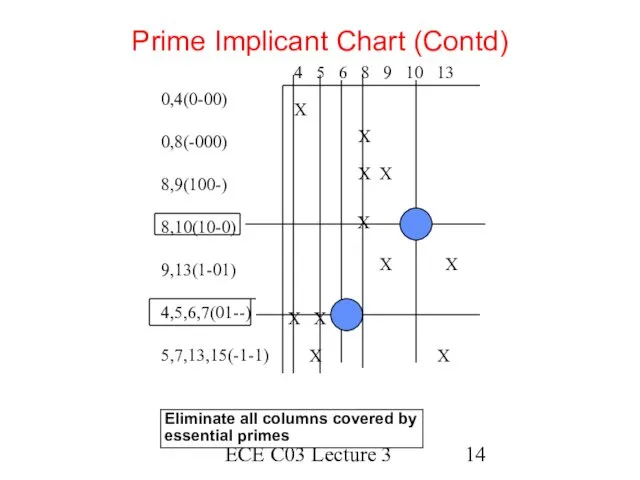
- 14. ECE C03 Lecture 3 Prime Implicant Chart (Contd) Eliminate all columns covered by essential primes 4
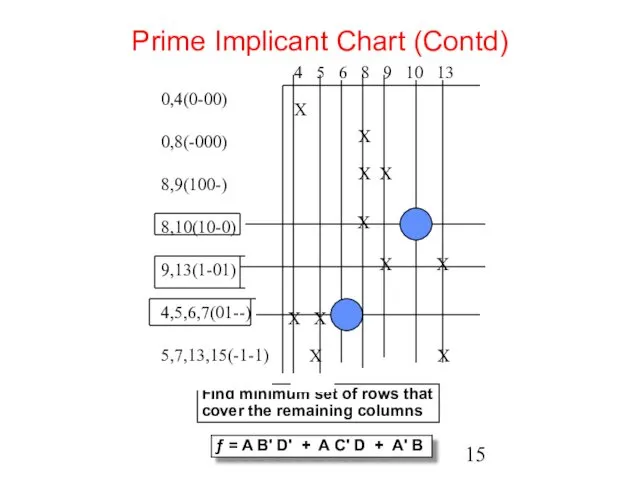
- 15. ECE C03 Lecture 3 Prime Implicant Chart (Contd) Find minimum set of rows that cover the
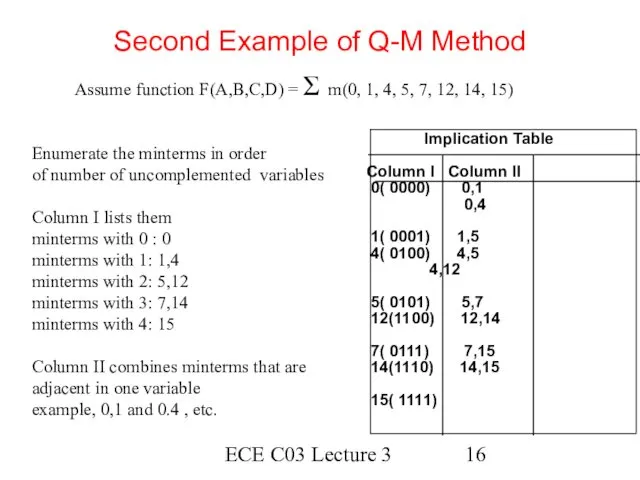
- 16. ECE C03 Lecture 3 Second Example of Q-M Method Assume function F(A,B,C,D) = Σ m(0, 1,
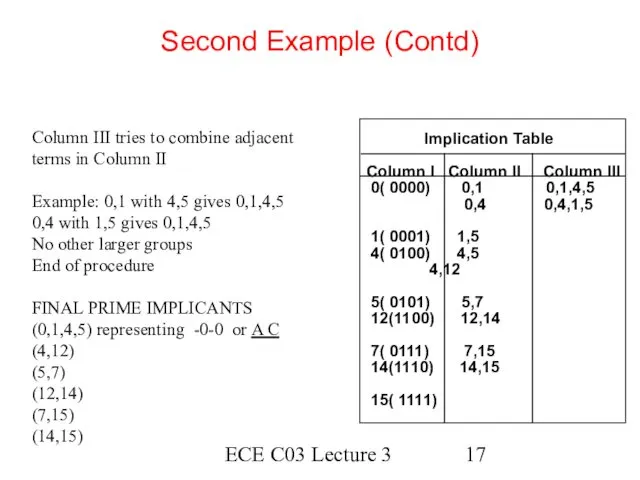
- 17. ECE C03 Lecture 3 Second Example (Contd) Implication Table Column I Column II Column III 0(
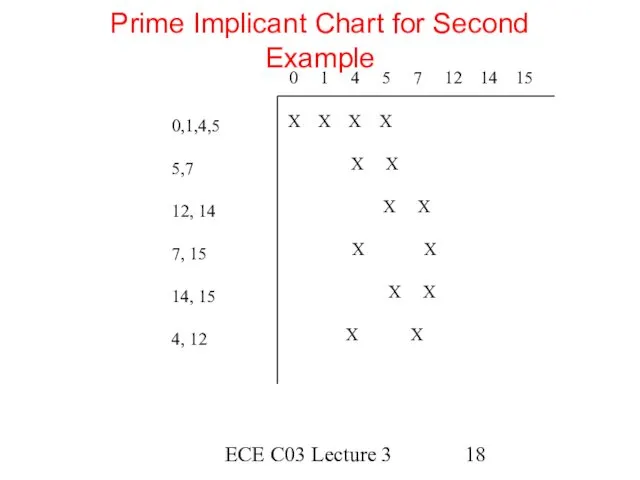
- 18. ECE C03 Lecture 3 Prime Implicant Chart for Second Example 0 1 4 5 7 12
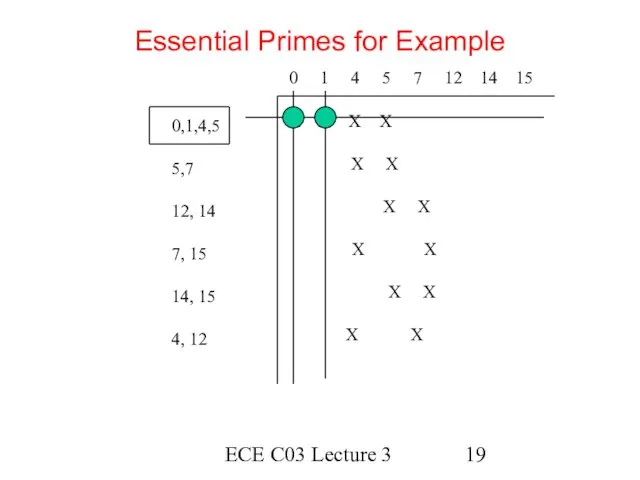
- 19. ECE C03 Lecture 3 Essential Primes for Example 0 1 4 5 7 12 14 15
- 20. ECE C03 Lecture 3 Delete Columns Covered by Essential Primes 0 1 4 5 7 12
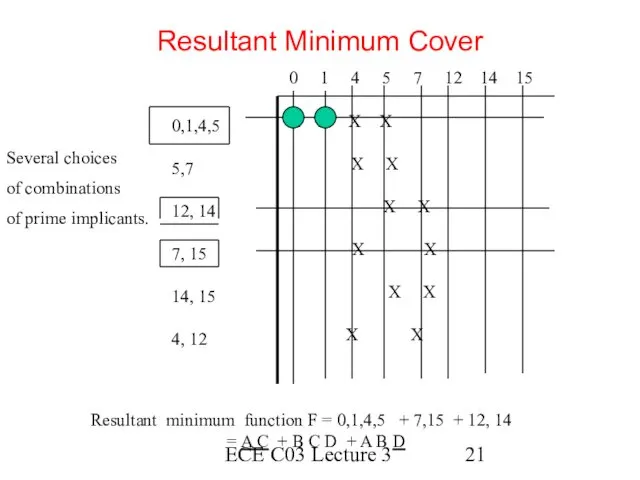
- 21. ECE C03 Lecture 3 Resultant Minimum Cover 0 1 4 5 7 12 14 15 0,1,4,5
- 22. ECE C03 Lecture 3 ESPRESSO Method Problem with Quine-McCluskey: the number of prime implicants grows rapidly
- 23. ECE C03 Lecture 3 Boolean Space The notion of redundancy can be formulated in Boolean space
- 24. ECE C03 Lecture 3 Boolean Space If g and h are two Boolean functions such that
- 25. ECE C03 Lecture 3 Redundancy in Boolean Space x1 x2 is said to cover x1 x2
- 26. ECE C03 Lecture 3 Minimizing Two Level Functions Sometimes just finding an irredundant cover may not
- 27. ECE C03 Lecture 3 Espresso Algorithm 1. Expands implicants to their maximum size Implicants covered by
- 28. ECE C03 Lecture 3 Details of ESPRESSO Algorithm Procedure ESPRESSO ( F, D, R) /* F
- 29. ECE C03 Lecture 3 Need for Iterations in ESPRESSO Espresso: Why Iterate on Reduce, Irredundant Cover,
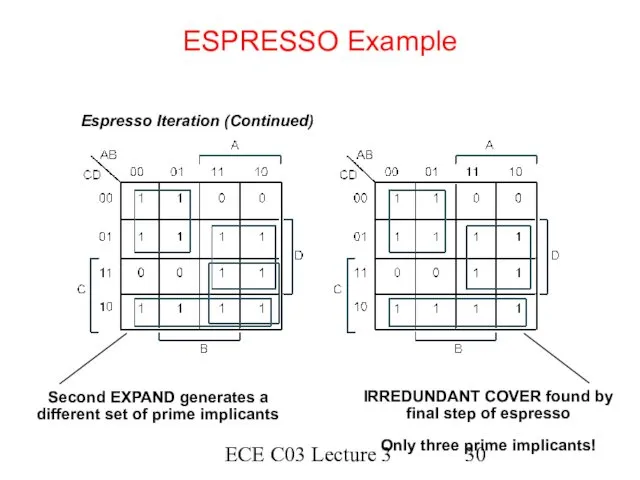
- 30. ECE C03 Lecture 3 ESPRESSO Example Espresso Iteration (Continued) Second EXPAND generates a different set of
- 31. ECE C03 Lecture 3 Example of ESPRESSO Input/Output .i 4 .o 1 .ilb a b c
- 32. ECE C03 Lecture 3 Two-Level Logic Design Approach Primitive logic building blocks INVERTER, AND, OR, NAND,
- 33. ECE C03 Lecture 3 SOP and POS Two-Level Logic Forms We have looked at two-level logic
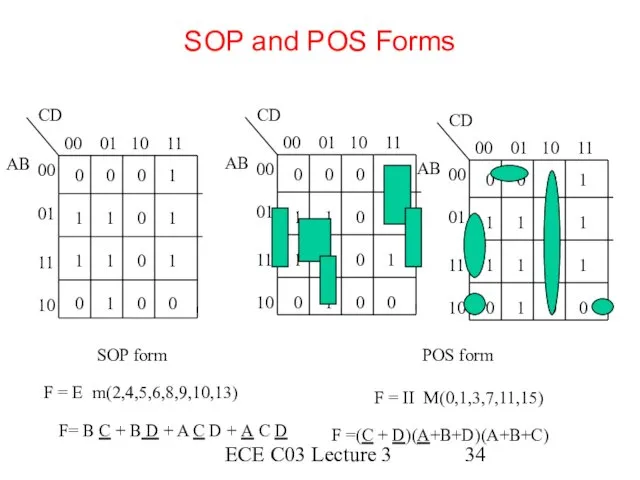
- 34. ECE C03 Lecture 3 SOP and POS Forms SOP form F = Ε m(2,4,5,6,8,9,10,13) POS form
- 35. ECE C03 Lecture 3 Product of Sums Minimization For a given function shown as a K-map,
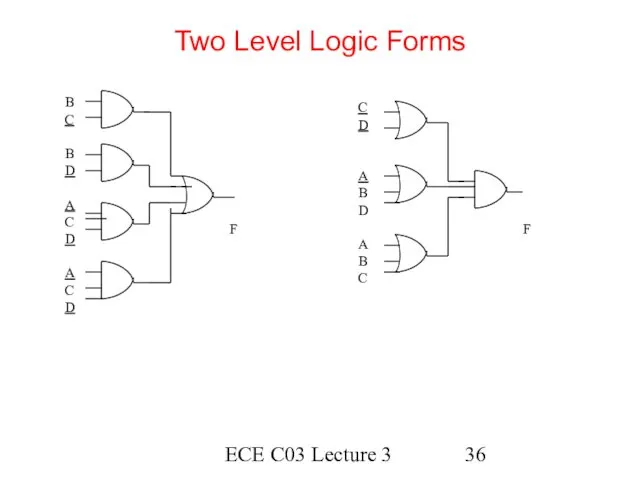
- 36. ECE C03 Lecture 3 Two Level Logic Forms B C B D A C D A
- 38. Скачать презентацию




















 Визуализация данных. Правила оформления таблиц
Визуализация данных. Правила оформления таблиц Элементы алгебры логики. Математические основы информатики
Элементы алгебры логики. Математические основы информатики Двовимірні масиви
Двовимірні масиви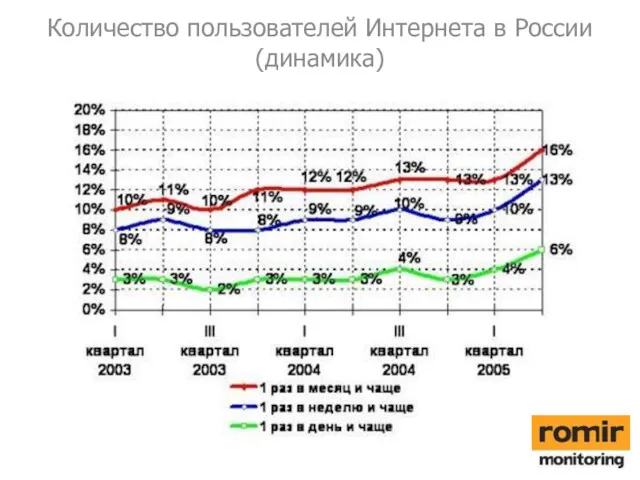 Количество пользователей Интернета в России (динамика)
Количество пользователей Интернета в России (динамика) Комплекс информационных систем, обеспечивающих автоматизированное ведение реестров маршрутов
Комплекс информационных систем, обеспечивающих автоматизированное ведение реестров маршрутов DS. Графический дизайн. Дизайн сайтов
DS. Графический дизайн. Дизайн сайтов Представление целых и вещественных чисел
Представление целых и вещественных чисел Понятие данных в информационных системах
Понятие данных в информационных системах Зачем человек приходит в этот мир?
Зачем человек приходит в этот мир? Информатика для детей
Информатика для детей Моделирование одежды в реальном времени
Моделирование одежды в реальном времени Текст для сайта. Сервис Shato
Текст для сайта. Сервис Shato Хранение и обработка информации в базах данных
Хранение и обработка информации в базах данных SDLC models and methodologies
SDLC models and methodologies Threads. Выполнение инструкций потоками
Threads. Выполнение инструкций потоками Прикладное программное обеспечение. (Тема 8)
Прикладное программное обеспечение. (Тема 8) Хранение информации
Хранение информации Программно-аппаратный комплекс для мониторинга и управления освещением в производственных помещениях
Программно-аппаратный комплекс для мониторинга и управления освещением в производственных помещениях Информационные технологии управления
Информационные технологии управления Системы управления базами данных. (Лекция 1)
Системы управления базами данных. (Лекция 1) Вводный урок по теме Создание и использование текстового редактора
Вводный урок по теме Создание и использование текстового редактора Безопасность банковской деятельности
Безопасность банковской деятельности Мозг и сеть. А где я?
Мозг и сеть. А где я? Общие правила оформления презентации информационных слайдов
Общие правила оформления презентации информационных слайдов Интерфейс Adobe Photoshop
Интерфейс Adobe Photoshop Логическая модель представления знаний
Логическая модель представления знаний Пользовательские типы данных
Пользовательские типы данных Текстовий процесор. 5 класс
Текстовий процесор. 5 класс