Содержание
- 2. Dynamic Programming
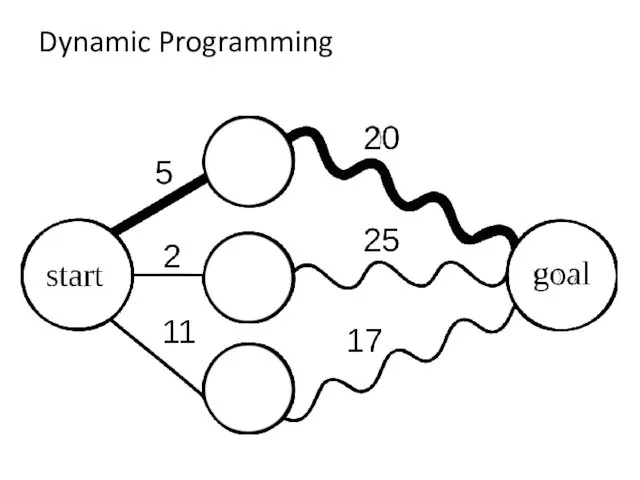
- 3. Dynamic Programming Dynamic Programming is mainly an optimization over plain recursion. Wherever we see a recursive
- 4. Dynamic Programming For example, if we write simple recursive solution for Fibonacci Numbers, we get exponential
- 5. Dynamic Programming 1 Introduction In this lecture we introduce dynamic programming, which is a high-level computational
- 6. Dynamic Programming In order to apply dynamic programming, we generally look for the following conditions: The
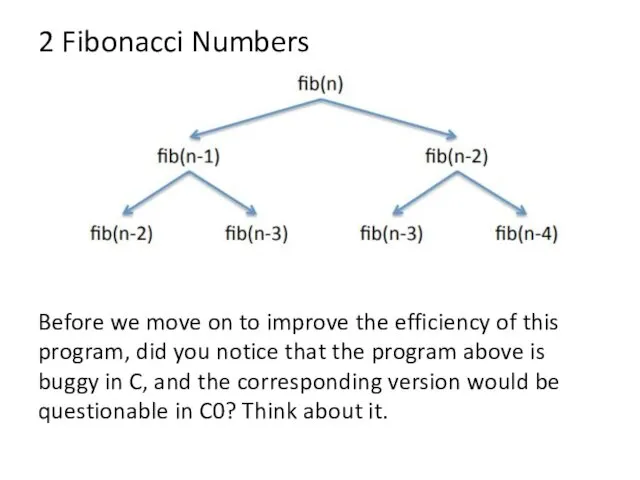
- 7. 2 Fibonacci Numbers As a very simple example, we consider the computation of the Fibonacci numbers.
- 8. 2 Fibonacci Numbers A direct (and very inefficient) implementation is a recursive function int fib0(int n)
- 9. 2 Fibonacci Numbers Before we move on to improve the efficiency of this program, did you
- 10. 2 Fibonacci Numbers The problem is that addition can overflow. In C, the result is undefined,
- 11. 2 Fibonacci Numbers #include int safe_plus(int x, int y) { if ( (x > 0 &&
- 12. 3 Top-Down Dynamic Programming In top-down dynamic programming we store the values as we compute them
- 13. 3 Top-Down Dynamic Programming int fib2_rec(int n, int* A) { REQUIRES(n >= 0); if (n ==
- 14. 3 Top-Down Dynamic Programming We also call this programming technique memoization. We might be tempted to
- 15. 4 Bottom-Up Dynamic Programming Top-down dynamic programming retains the structure of the original (inefficient) recursive function.
- 16. 4 Bottom-Up Dynamic Programming In our example, we would like to compute A[0], A[1], A[2], .
- 17. Program for Fibonacci numbers The Fibonacci numbers are the numbers in the following integer sequence. 0,
- 18. Method 1 ( Use recursion ) vs Method 2 ( Use Dynamic Programming ) Time Complexity:
- 19. Method 2 ( Use Dynamic Programming )
- 20. Method 3 ( Space Optimized Method 2 ) Time Complexity: linear O(n) Extra Space: O(1)
- 21. Method 4 ( Using power of the matrix {{1,1},{1,0}} ) This another O(n) which relies on
- 22. Method 4 ( Using power of the matrix {{1,1},{1,0}} ) #include /* Helper function that multiplies
- 23. Method 4 ( Using power of the matrix {{1,1},{1,0}} ) void multiply(int F[2][2], int M[2][2]) {
- 24. Method 4 ( Using power of the matrix {{1,1},{1,0}} ) /* Driver program to test above
- 25. Method 5 ( Optimized Method 4 ) The method 4 can be optimized to work in
- 26. Method 5 ( Optimized Method 4 ) void multiply(int F[2][2], int M[2][2]) { int x =
- 27. Method 6 (O(Log n) Time) Below is one more interesting recurrence formula that can be used
- 28. Method 6 (O(Log n) Time) Time complexity of this solution is O(Log n)
- 29. Method 7 Another approach:(Using formula) In this method we directly implement the formula for nth term
- 30. 5 BDD & ROBDD In computer science, a binary decision diagram (BDD) or branching program is
- 31. 5 Implementing ROBDDs In the implementation of ROBDDs, dynamic programming plays a pervasive role. Binary decision
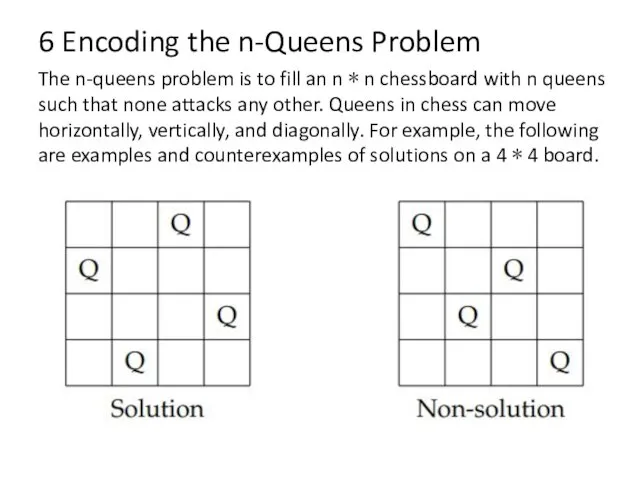
- 32. 6 Encoding the n-Queens Problem The n-queens problem is to fill an n ∗ n chessboard
- 33. 6 Encoding the n-Queens Problem We would like to encode n-queens problems as ROBDDS. The idea
- 34. 6 Encoding the n-Queens Problem For example, to encode that the column 0 has at least
- 35. 6 Encoding the n-Queens Problem typedef struct bdd* bdd; typedef int bdd_node; bdd bdd_new(int k); /*
- 36. 6 Encoding the n-Queens Problem The crucial functions here are make and apply. make(B, x, u,
- 37. 6 Encoding the n-Queens Problem apply(B, op, u, v) takes two BDD nodes u and v
- 38. 6 Encoding the n-Queens Problem bdd B = bdd_new(4*4); int x00 = make(B, 1, 0, 1);
- 40. Скачать презентацию






















![Method 5 ( Optimized Method 4 ) void multiply(int F[2][2],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/21015/slide-25.jpg)











 Позиционные системы счисления
Позиционные системы счисления Локальные сети. Параметры сетей и их стандарты
Локальные сети. Параметры сетей и их стандарты Сбор и подготовка данных
Сбор и подготовка данных Современные накопители информации, используемые в вычислительной технике
Современные накопители информации, используемые в вычислительной технике Использование технологии веб-квест как средство развития познавательных и творческих способностей учащихся
Использование технологии веб-квест как средство развития познавательных и творческих способностей учащихся Блочные алгоритмы. Блочное шифрование. Сравнение блочных и поточных шифров. Предпосылки создания шифра Фейстеля
Блочные алгоритмы. Блочное шифрование. Сравнение блочных и поточных шифров. Предпосылки создания шифра Фейстеля Параллельное программирование. С++. Thread Support Library. Atomic Operations Library
Параллельное программирование. С++. Thread Support Library. Atomic Operations Library Функции в Excel
Функции в Excel Организация и средства информационных технологий обеспечения управленческой деятельности
Организация и средства информационных технологий обеспечения управленческой деятельности Поиск публикаций и показатели деятельности ученого в Web of Science
Поиск публикаций и показатели деятельности ученого в Web of Science Бездротові мережі
Бездротові мережі Занятие 1. Знакомство с программой Adobe Photoshop
Занятие 1. Знакомство с программой Adobe Photoshop Microsoft Visual Studio — линейка продуктов компании Microsoft
Microsoft Visual Studio — линейка продуктов компании Microsoft Операторы цикла
Операторы цикла Понятие об информации. Представление информации. Информационная деятельность человека.
Понятие об информации. Представление информации. Информационная деятельность человека. Автоматизоване створення запитів у базі даних
Автоматизоване створення запитів у базі даних Архітектура операційних систем
Архітектура операційних систем Windows System Programming
Windows System Programming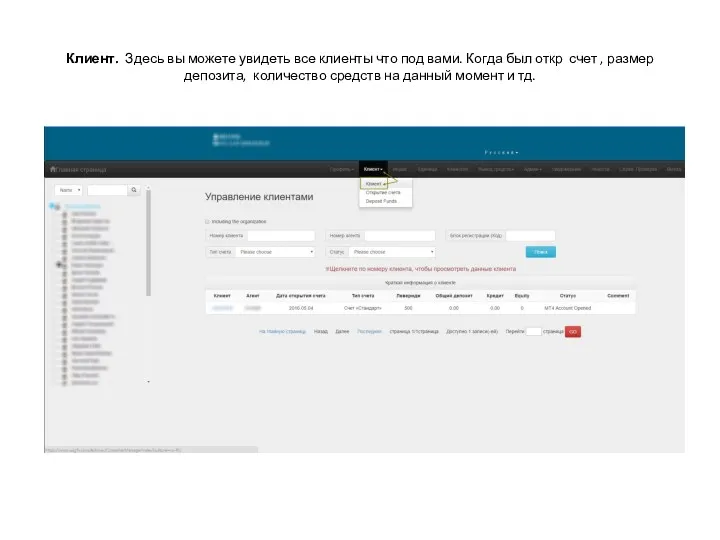 Личный кабинет
Личный кабинет Мир станочника. Аддитивные технологии и 3D-сканирование
Мир станочника. Аддитивные технологии и 3D-сканирование Методы и средства защиты программ от компьютерных вирусов
Методы и средства защиты программ от компьютерных вирусов 46_Yaroslavskaya_Sasha
46_Yaroslavskaya_Sasha Локальные и глобальные сети ЭВМ. Защита информации в сетях. (Тема 6)
Локальные и глобальные сети ЭВМ. Защита информации в сетях. (Тема 6) Godseeker. Игра
Godseeker. Игра Рабочий стол. Управление компьютером с помощью мыши
Рабочий стол. Управление компьютером с помощью мыши Проектирование изделий из листового металла в NX
Проектирование изделий из листового металла в NX Эти люди изменили мир
Эти люди изменили мир Электронные ресурсы для детей и юношества в общедоступных библиотеках: создание и использование
Электронные ресурсы для детей и юношества в общедоступных библиотеках: создание и использование