Содержание
- 2. Содержание Определение структуры Связь АА-деревьев с другими деревьями поиска История структуры Свойства АА-деревьев Основные операции для
- 3. Определение структуры АА-дерево – это форма сбалансированного дерева, которое используется для хранения и эффективного извлечения упорядоченных
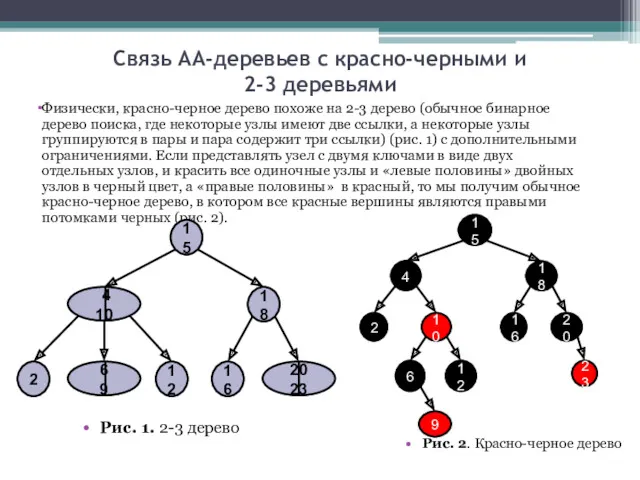
- 4. Связь АА-деревьев с красно-черными и 2-3 деревьями Физически, красно-черное дерево похоже на 2-3 дерево (обычное бинарное
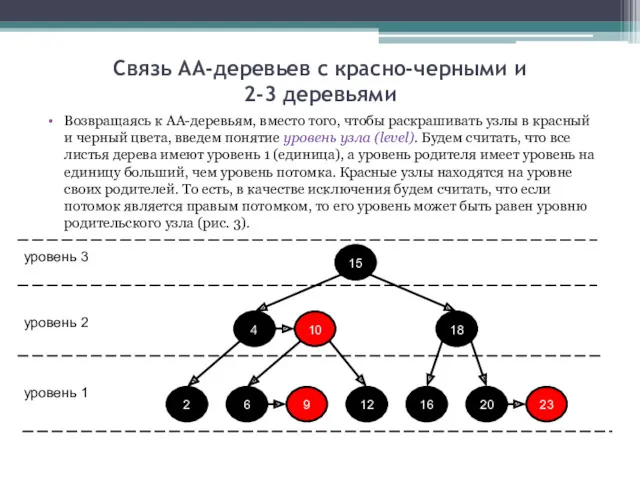
- 5. Связь АА-деревьев с красно-черными и 2-3 деревьями Возвращаясь к АА-деревьям, вместо того, чтобы раскрашивать узлы в
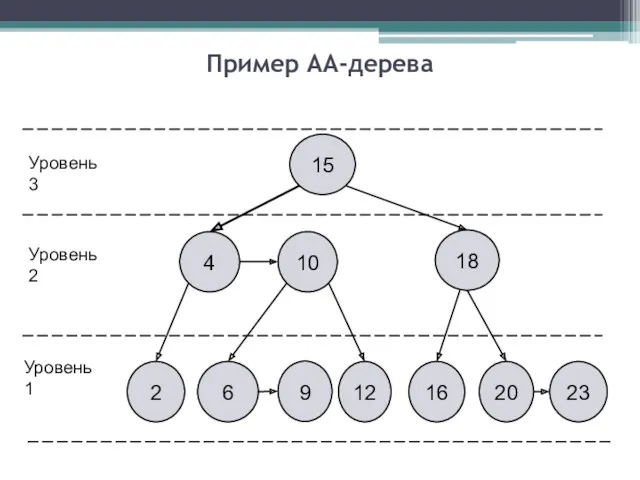
- 6. Пример АА-дерева
- 7. История структуры AA-дерево было придумано Арне Андерссоном в 1993 году, который первым решил, что для упрощения
- 8. Свойства АА-дерева Уровень листа равен 1. Уровень левого потомка строго меньше уровня узла. Уровень правого потомка
- 9. Описание структуры АА-дерева : type pl_tree = ^el_tree; el_tree = record key : integer; level :
- 10. ОСНОВНЫЕ ОПЕРАЦИИ ДЛЯ РАБОТЫ С АА-ДЕРЕВОМ И АЛГОРИТМЫ ИХ РЕАЛИЗАЦИИ Для балансировки АА-дерева нужно всего 2
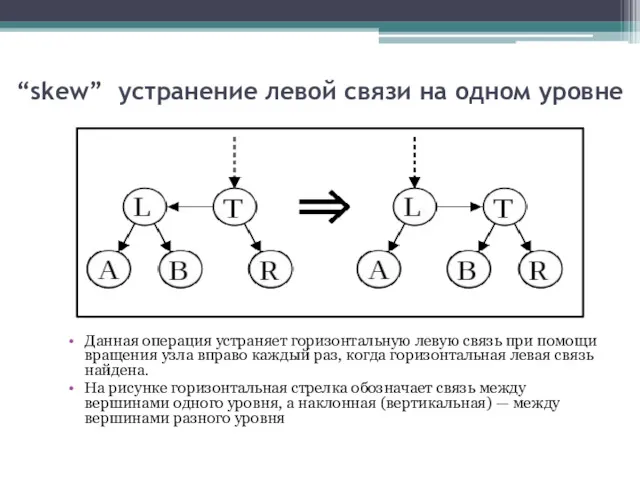
- 11. “skew” устранение левой связи на одном уровне Данная операция устраняет горизонтальную левую связь при помощи
- 12. Код процедуры “skew” procedure Skew_t (var t : pl_tree); var tmp : pl_tree; begin if t
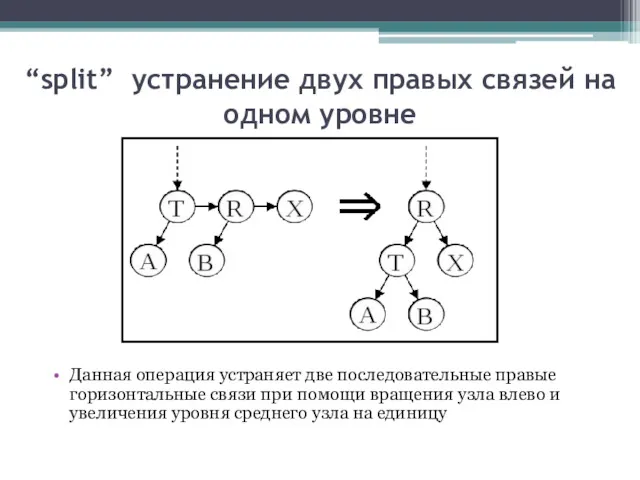
- 13. “split” устранение двух правых связей на одном уровне Данная операция устраняет две последовательные правые горизонтальные
- 14. Код процедуры “split” procedure Split_t (var t : pl_tree); var tmp : pl_tree; begin if t
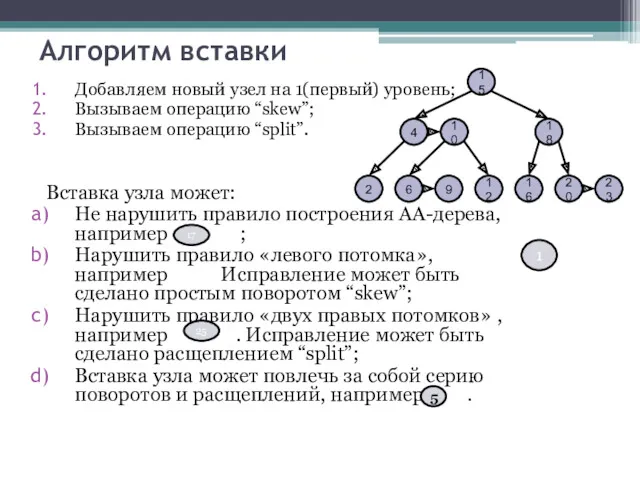
- 15. Алгоритм вставки Добавляем новый узел на 1(первый) уровень; Вызываем операцию “skew”; Вызываем операцию “split”. Вставка узла
- 16. Вставка элемента в дерево procedure Insert_Node (var root_f : pl_tree; x : integer); begin if root_f
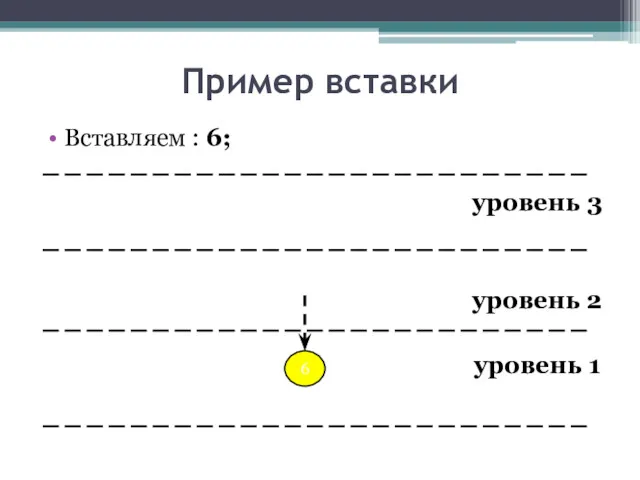
- 17. Пример вставки Вставляем : 6; уровень 3 уровень 2 уровень 1 6
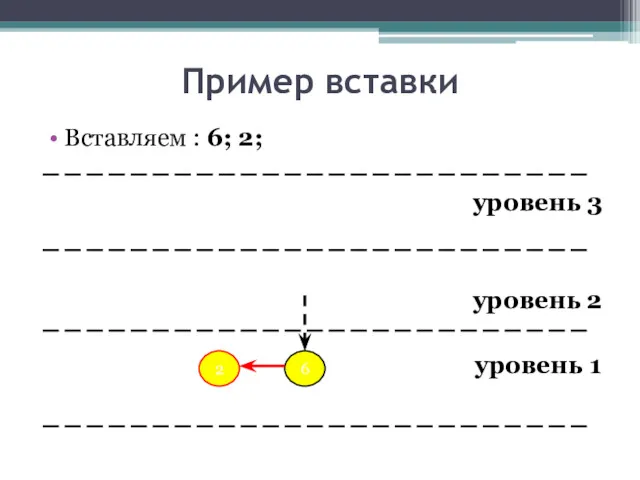
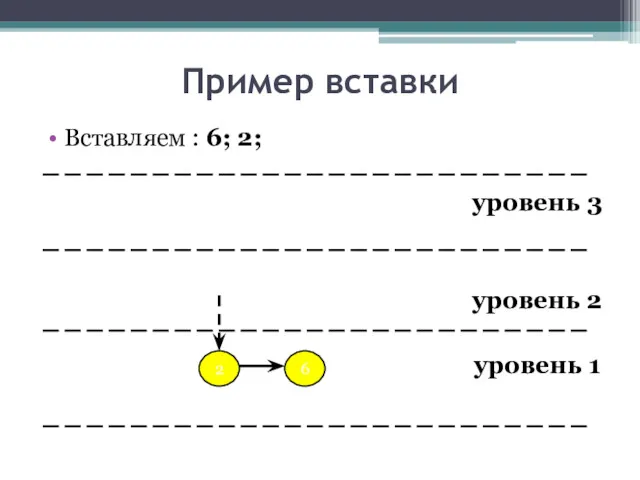
- 18. Пример вставки Вставляем : 6; 2; уровень 3 уровень 2 уровень 1 6 2
- 19. Пример вставки Вставляем : 6; 2; уровень 3 уровень 2 уровень 1 6 2
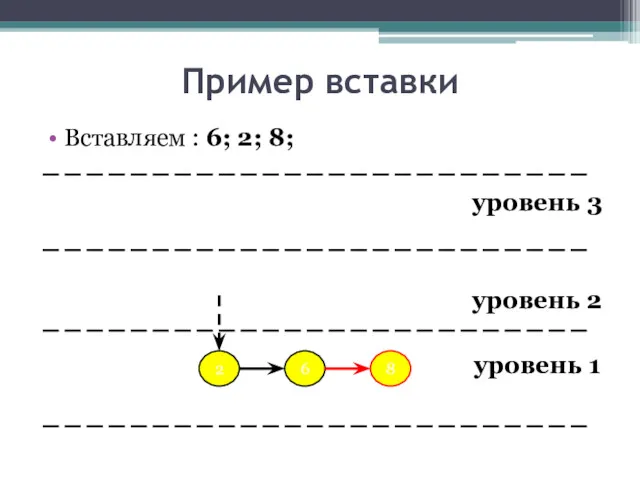
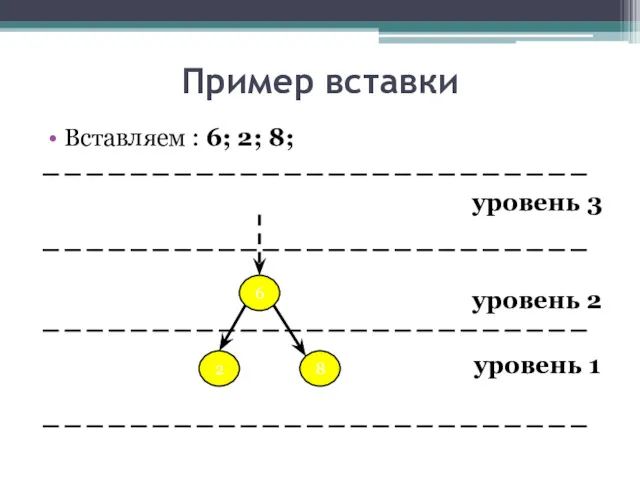
- 20. Пример вставки Вставляем : 6; 2; 8; уровень 3 уровень 2 уровень 1 6 2 8
- 21. Пример вставки Вставляем : 6; 2; 8; уровень 3 уровень 2 уровень 1 6 2 8
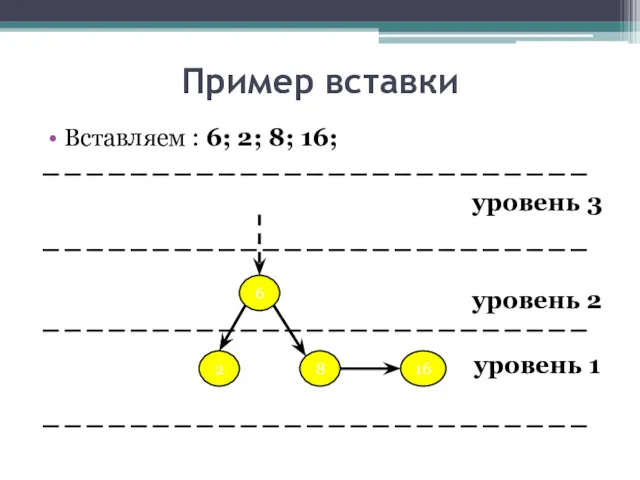
- 22. Пример вставки Вставляем : 6; 2; 8; 16; уровень 3 уровень 2 уровень 1 6 2
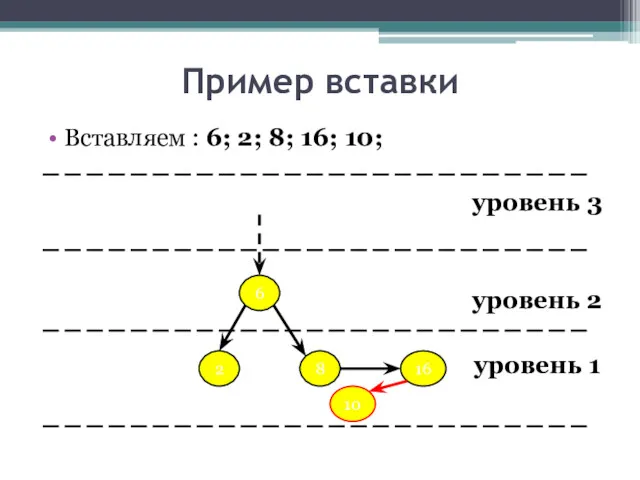
- 23. Пример вставки Вставляем : 6; 2; 8; 16; 10; уровень 3 уровень 2 уровень 1 6
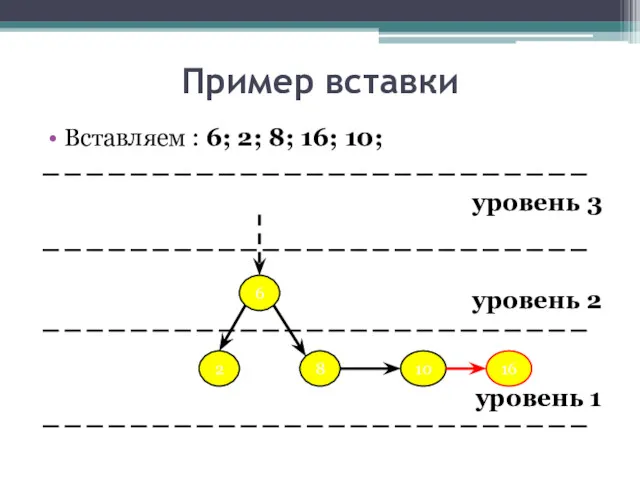
- 24. Пример вставки Вставляем : 6; 2; 8; 16; 10; уровень 3 уровень 2 уровень 1 6
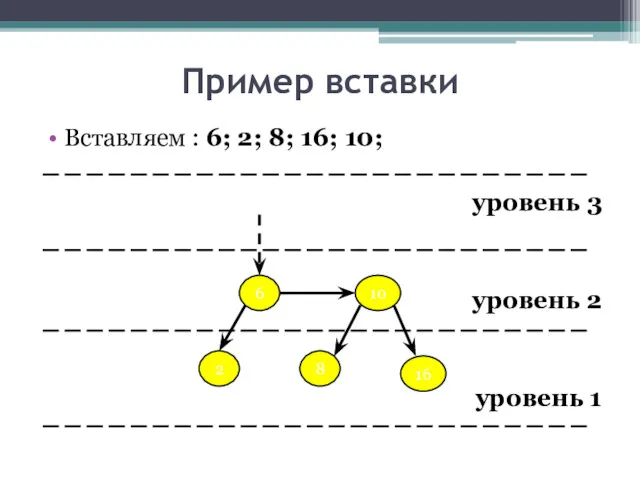
- 25. Пример вставки Вставляем : 6; 2; 8; 16; 10; уровень 3 уровень 2 уровень 1 6
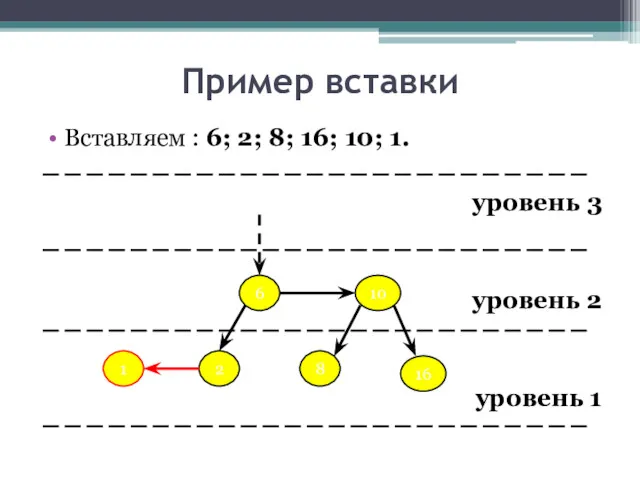
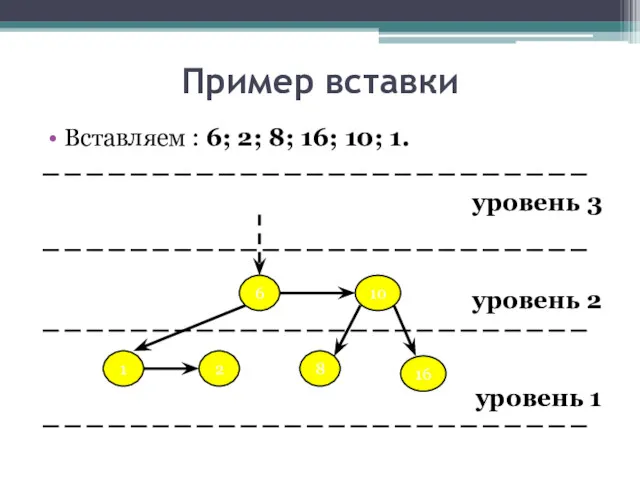
- 26. Пример вставки Вставляем : 6; 2; 8; 16; 10; 1. уровень 3 уровень 2 уровень 1
- 27. Пример вставки Вставляем : 6; 2; 8; 16; 10; 1. уровень 3 уровень 2 уровень 1
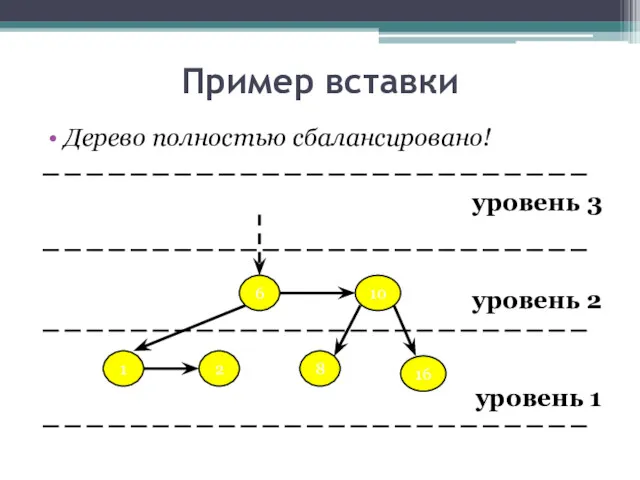
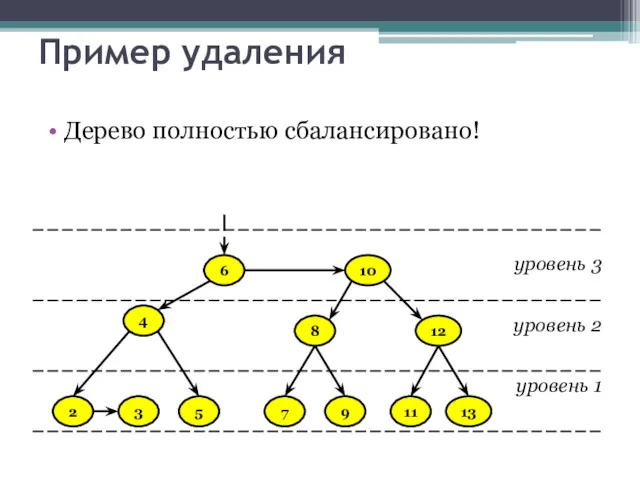
- 28. Пример вставки Дерево полностью сбалансировано! уровень 3 уровень 2 уровень 1 6 2 8 16 10
- 29. Алгоритм удаления Удаление элемента также производится по правилам удаления из обычного двоичного дерева поиска с последующей
- 30. Удаление элемента procedure Delete_Node (var root_f : pl_tree; newkey : integer); begin if root_f nil then
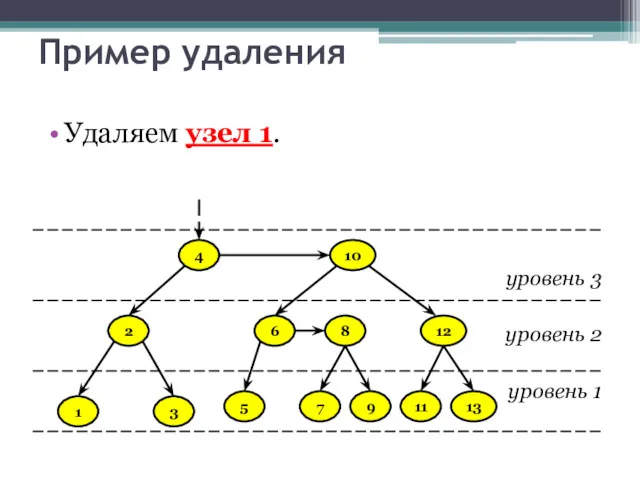
- 31. Пример удаления Удаляем узел 1. уровень 3 уровень 2 уровень 1 10 8 6 9 7
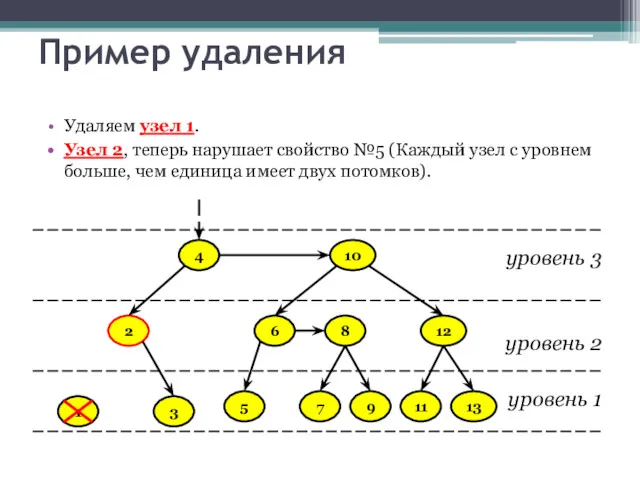
- 32. Пример удаления Удаляем узел 1. Узел 2, теперь нарушает свойство №5 (Каждый узел с уровнем больше,
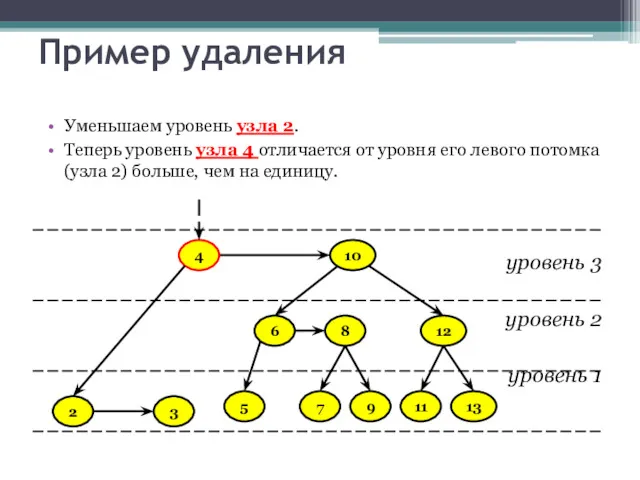
- 33. Пример удаления Уменьшаем уровень узла 2. Теперь уровень узла 4 отличается от уровня его левого потомка(узла
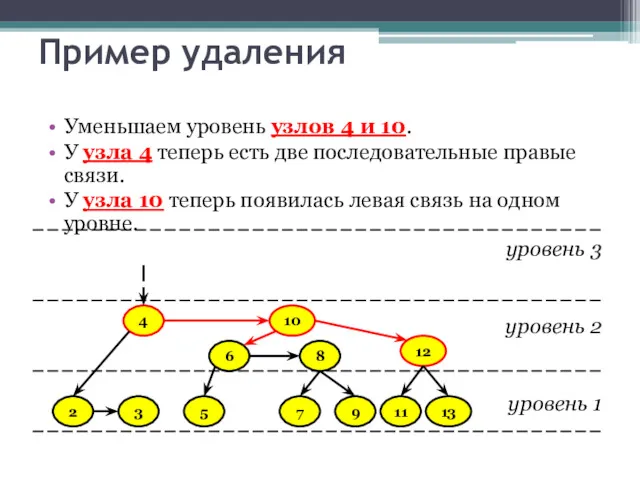
- 34. Пример удаления Уменьшаем уровень узлов 4 и 10. У узла 4 теперь есть две последовательные правые
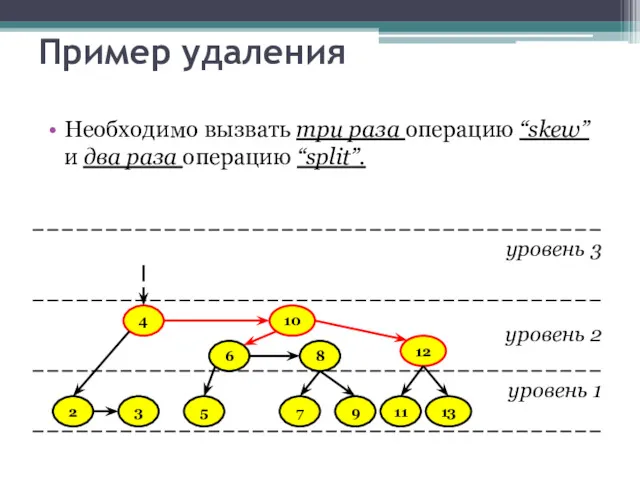
- 35. Пример удаления Необходимо вызвать три раза операцию “skew” и два раза операцию “split”. уровень 3 уровень
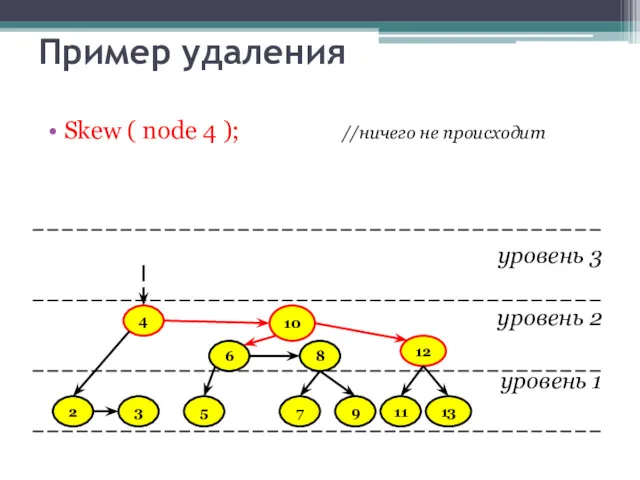
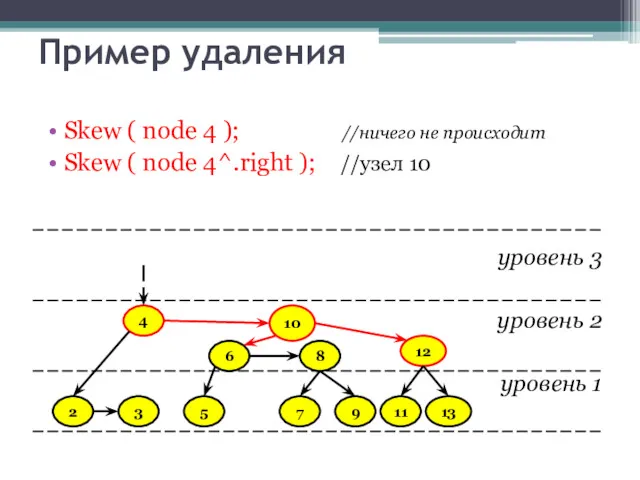
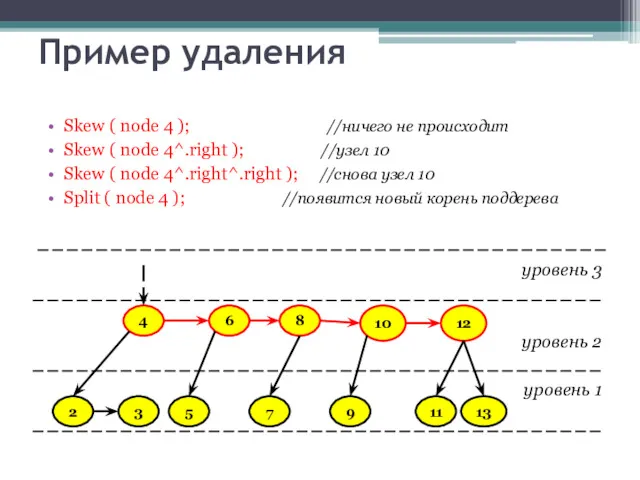
- 36. Пример удаления Skew ( node 4 ); //ничего не происходит уровень 3 уровень 2 уровень 1
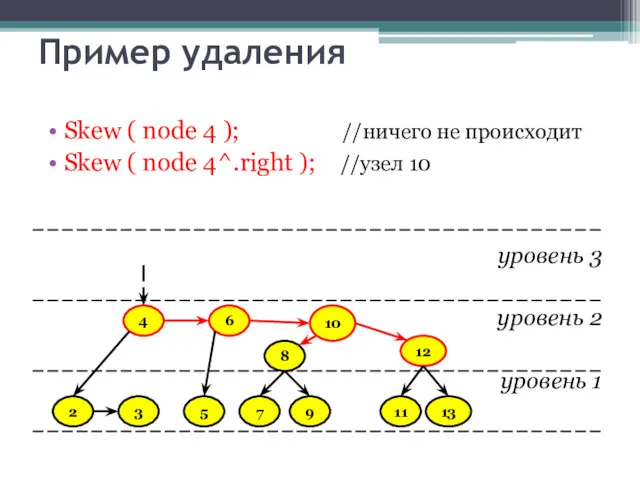
- 37. Пример удаления Skew ( node 4 ); //ничего не происходит Skew ( node 4^.right ); //узел
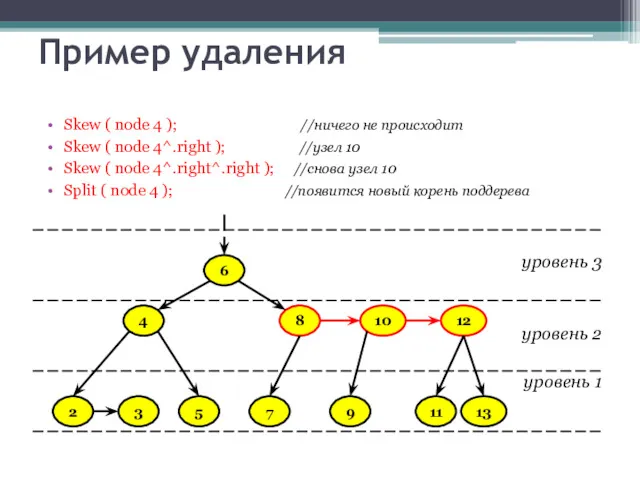
- 38. Пример удаления Skew ( node 4 ); //ничего не происходит Skew ( node 4^.right ); //узел
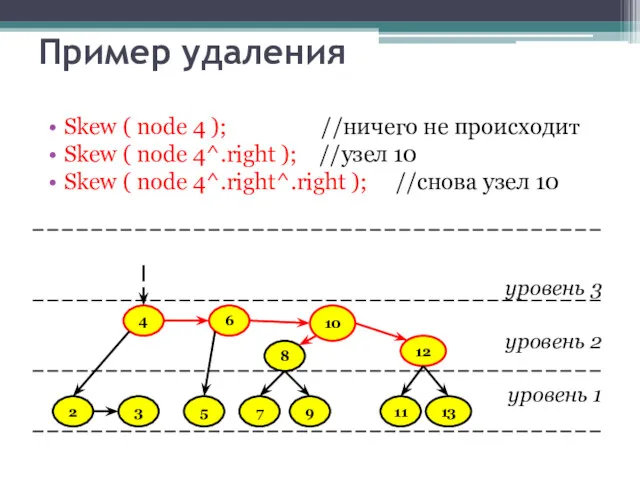
- 39. Пример удаления Skew ( node 4 ); //ничего не происходит Skew ( node 4^.right ); //узел
- 40. Пример удаления Skew ( node 4 ); //ничего не происходит Skew ( node 4^.right ); //узел
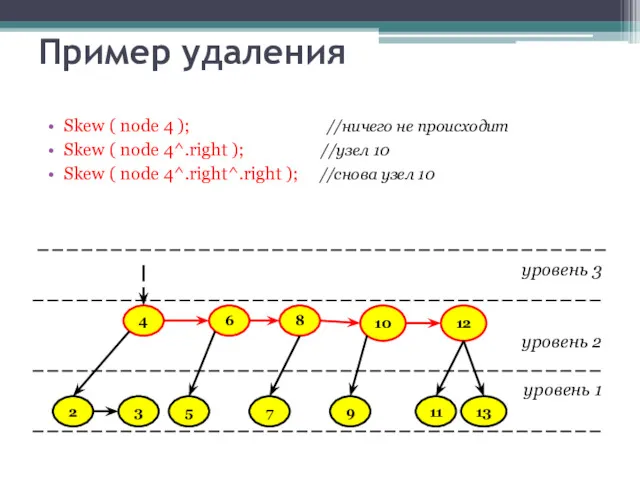
- 41. Пример удаления Skew ( node 4 ); //ничего не происходит Skew ( node 4^.right ); //узел
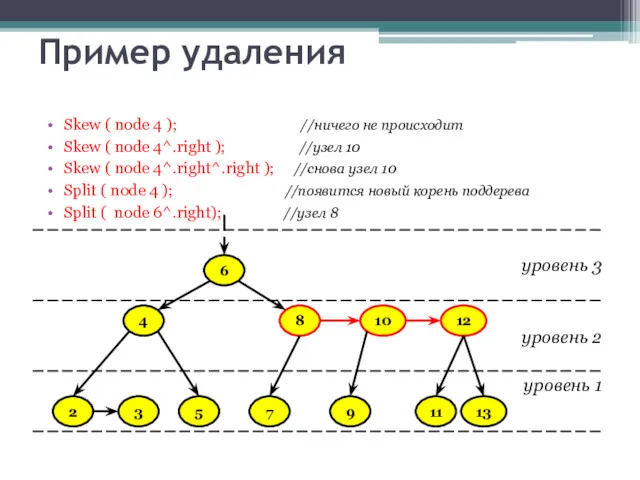
- 42. Пример удаления Skew ( node 4 ); //ничего не происходит Skew ( node 4^.right ); //узел
- 43. Пример удаления Skew ( node 4 ); //ничего не происходит Skew ( node 4^.right ); //узел
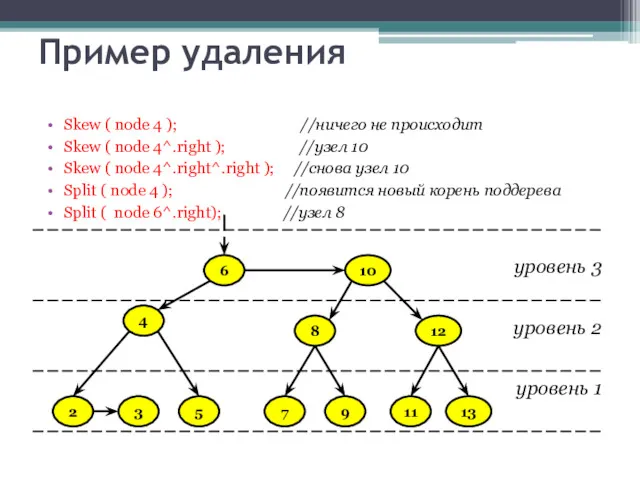
- 44. Пример удаления Skew ( node 4 ); //ничего не происходит Skew ( node 4^.right ); //узел
- 45. Пример удаления Дерево полностью сбалансировано! уровень 3 уровень 2 уровень 1 10 8 6 9 7
- 46. Заключение В своей работе Арне Андерссон делает вывод, что если сравнивать по производительности четыре типа двоичных
- 47. СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ И ИСТОЧНИКОВ AA-Tree – http://en.wikipedia.org/wiki/AA_tree. AA-Tree или простое бинарное дерево – http://habrahabr.ru/post/110212 .
- 49. Скачать презентацию













 Математика в повседневной жизни
Математика в повседневной жизни Умножение
Умножение Взаимное расположение прямой и окружности. 8 класс
Взаимное расположение прямой и окружности. 8 класс Квадратичная функция и её свойства
Квадратичная функция и её свойства S и p фигуры
S и p фигуры Урок математики во 2 классе Решение задач
Урок математики во 2 классе Решение задач Метод координат. Геометрия 9 класс
Метод координат. Геометрия 9 класс Презентация к уроку математики во 2 классе по теме: Час.Минута. Определение времени по часам
Презентация к уроку математики во 2 классе по теме: Час.Минута. Определение времени по часам Математик уеннар
Математик уеннар Метрические свойства проекций. (Лекция 3)
Метрические свойства проекций. (Лекция 3) Тождественные преобразования тригонометрических выражений
Тождественные преобразования тригонометрических выражений Теория вероятностей; геометрическая вероятность; неравенство Чебышева
Теория вероятностей; геометрическая вероятность; неравенство Чебышева Решение задач разными способами
Решение задач разными способами Пути в графе. Связные графы
Пути в графе. Связные графы Угол. Виды углов. 4 класс
Угол. Виды углов. 4 класс Solving linear recurrence relations
Solving linear recurrence relations Многокутник та його елементи. 8 клас
Многокутник та його елементи. 8 клас Решение заданий В10 по материалам открытого банка задач ЕГЭ по математике 2013 года
Решение заданий В10 по материалам открытого банка задач ЕГЭ по математике 2013 года урок математики 4 класс Решение задач на одновременное движение двух объектов в противоположных направлениях
урок математики 4 класс Решение задач на одновременное движение двух объектов в противоположных направлениях урок математики в 3 классе Умножение многозначного на однозначное число по программе Начальная школа 21 век
урок математики в 3 классе Умножение многозначного на однозначное число по программе Начальная школа 21 век Виды углов. Измерение углов
Виды углов. Измерение углов Понятие процента. Правило чтения процента. Нахождение процента от числа. Нахождение числа по его процентам
Понятие процента. Правило чтения процента. Нахождение процента от числа. Нахождение числа по его процентам Второй признак равенства треугольников
Второй признак равенства треугольников Смежные и вертикальные углы
Смежные и вертикальные углы Теорема Пифагора
Теорема Пифагора Foundation Year Program NUFYP Mathematics
Foundation Year Program NUFYP Mathematics Трапеция. Свойства
Трапеция. Свойства Исследовательская работа на тему Изопериметрические задачи
Исследовательская работа на тему Изопериметрические задачи