Содержание
- 2. Запишите в виде математического выражения: х на 5 больше y х в пять раз больше y
- 3. х больше, чем у на 5 Разница между ними равна пяти. Значит, чтобы получить бóльшую величину,
- 4. х больше, чем у, в пять раз Значит, если у умножить на 5, получим х. х
- 5. z меньше x в 3,5 раза z = или х = 3,5z * Повторим терминологию Сумма
- 6. частное от деления a на b в полтора раза больше b a : b больше, чем
- 7. (х + у)2 = 7 квадрат суммы x и y равен 7 * x составляет 60
- 8. m больше n на 15 процентов Если n принять за 100%, то m на 15 процентов
- 9. Задачи на движение. Два правила: Все эти задачи решаются по одной-единственной формуле: s=vt, то есть расстояние
- 10. 1. Из пункта А в пункт В, расстояние между которыми 50 км, одновременно выехали автомобилист и
- 11. Решаем уравнение * Для первой дроби дополнительный множитель х+4, для второй - х Разделим обе части
- 12. Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 70
- 13. * X2 + 3x - 70 = 0 D = 9 + 4 ∙70 = 289
- 14. * Следующий тип задач — когда что-нибудь плавает по речке, в которой есть течение. Например, теплоход,
- 15. Моторная лодка прошла против течения реки 255 км и вернулась в пункт отправления, затратив на обратный
- 16. Решите уравнение! * Приводим дроби в левой части к одному знаменателю Раскрываем скобки Делим обе части
- 17. Теплоход проходит по течению реки до пункта назначения 200 км и после стоянки возвращается в пункт
- 18. * Прежде всего разделим обе части уравнения на 10. Оно станет проще! Не будем подробно останавливаться
- 19. Баржа в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А.
- 20. Получаем уравнение: * Число 4 в правой части представим в виде неправильной дроби: 4 = Приведем
- 21. * Задачи на работу решаются с помощью одной-единственной формулы: A =p ⋅ t A — работа,
- 22. Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в
- 23. Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в
- 24. Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит
- 25. * (х + у) ⋅ 12 = 1 2х = 3у 2х = 3у, у =
- 26. Всевозможные задачи про две трубы, которые наполняют какой-либо резервуар для воды — это тоже задачи на
- 28. Скачать презентацию

























 Вычитание удобным способом
Вычитание удобным способом Признаки деления на 3, на 9
Признаки деления на 3, на 9 Физкультминутка(презентация)
Физкультминутка(презентация) Транспортная задача
Транспортная задача Некоторые свойства прямоугольного треугольника. Урок 47
Некоторые свойства прямоугольного треугольника. Урок 47 Равные треугольники. Высота, биссектриса, медиана. 7 класс
Равные треугольники. Высота, биссектриса, медиана. 7 класс Формулы сокращенного умножения
Формулы сокращенного умножения устный счет
устный счет Сумматор
Сумматор Презентация Ох, уж эта математика
Презентация Ох, уж эта математика Свойства функции. 10 класс
Свойства функции. 10 класс Геометрический смысл производной. Подготовка к ЕГЭ
Геометрический смысл производной. Подготовка к ЕГЭ Сложение и вычитание в пределах 20
Сложение и вычитание в пределах 20 Счастливый случай. Игра
Счастливый случай. Игра Инновационный опыт
Инновационный опыт Задачи на нахождение значений параметра
Задачи на нахождение значений параметра Урок Чему я научился: умножать и делить во 2 классе. Обобщающий урок по математике, УМК Перспектива.
Урок Чему я научился: умножать и делить во 2 классе. Обобщающий урок по математике, УМК Перспектива. Прямоугольная система координат на плоскости. 6 класс
Прямоугольная система координат на плоскости. 6 класс Ряд натуральных чисел
Ряд натуральных чисел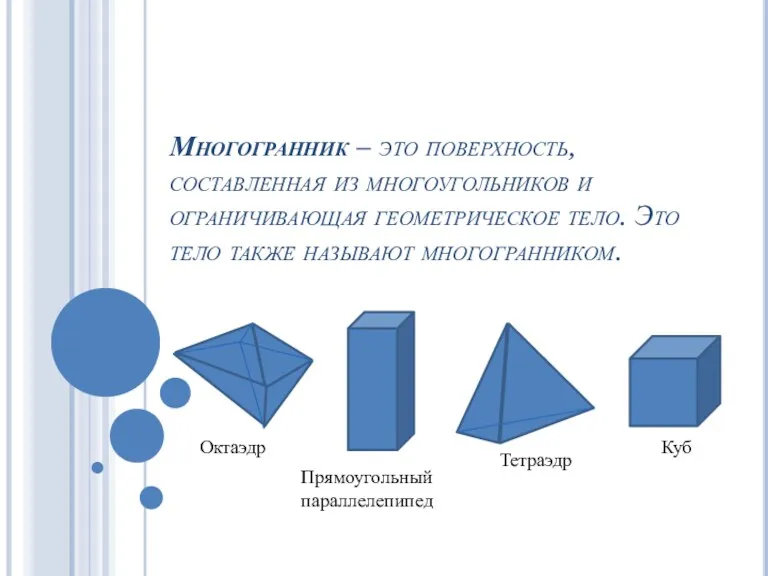 Многогранники и их виды
Многогранники и их виды Понятие движения в геометрии
Понятие движения в геометрии Системы двух уравнений с двумя неизвестными. 7 класс
Системы двух уравнений с двумя неизвестными. 7 класс Треугольники. Виды треугольников. Основные свойства треугольников
Треугольники. Виды треугольников. Основные свойства треугольников Decimals
Decimals Взаимно простые числа. Признак делимости на произведение
Взаимно простые числа. Признак делимости на произведение Сложение и вычитание векторов
Сложение и вычитание векторов устный счёт в виде теста 2 класс Табличное умножение
устный счёт в виде теста 2 класс Табличное умножение Перпендикулярные прямые. Решение задач
Перпендикулярные прямые. Решение задач