Содержание
- 2. Цель лекции – изучить основные положения теории булевых функций для использования точных методов анализа и синтеза
- 3. Горбатов В.А. Основы дискретной математики. М.: Высш. шк., 1986. 32-61с. Савельев А.Я. Прикладная теория цифровых автоматов.
- 4. Базовые понятия: множество законы (ассоциативный, коммутативный, элиминации, др.), бинарные и унарные операции, алгебра, двоичная система счисления
- 5. Родился в Линкольне 1849 – профессор математики Куинс-Колледжа в Корке (Ирландия) За работы в области высшего
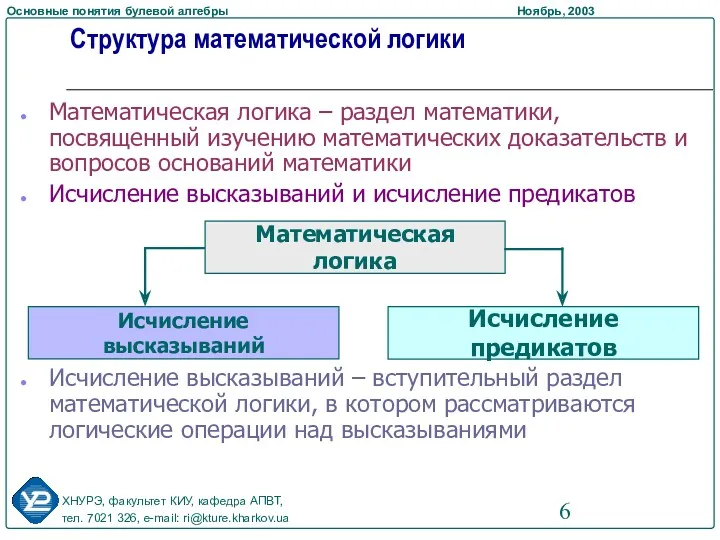
- 6. Структура математической логики Математическая логика – раздел математики, посвященный изучению математических доказательств и вопросов оснований математики
- 7. Булевы переменные и булевы функции В алгебре логики интересуются лишь истинностным значением высказываний Обозначения: 1 (истина)
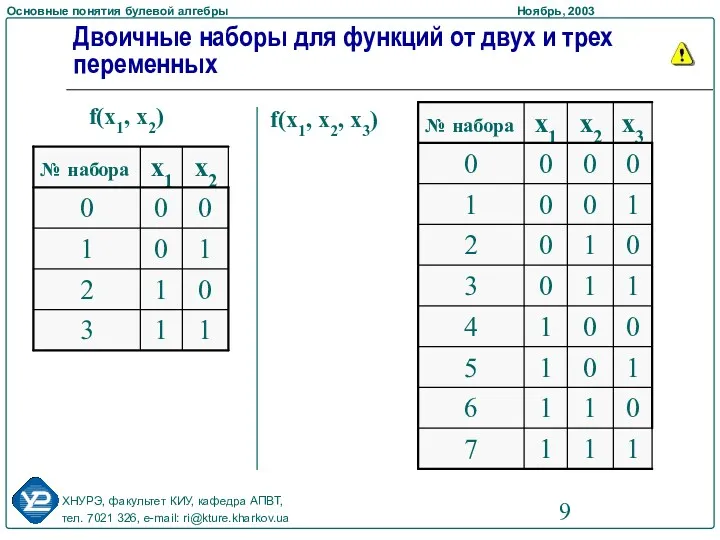
- 8. Двоичные наборы Переменные булевой функции образуют наборы из нулей и единиц. Такие наборы называют двоичными Сколько
- 9. Двоичные наборы для функций от двух и трех переменных f(x1, x2) f(x1, x2, x3)
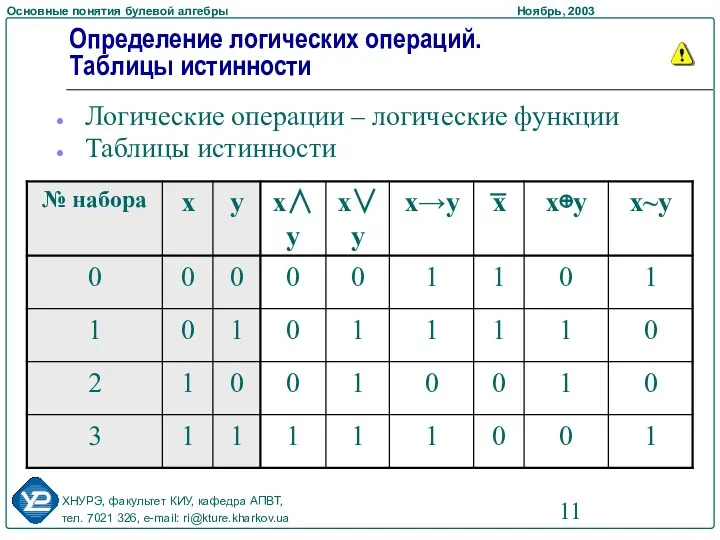
- 10. Логические операции
- 11. Определение логических операций. Таблицы истинности Логические операции – логические функции Таблицы истинности
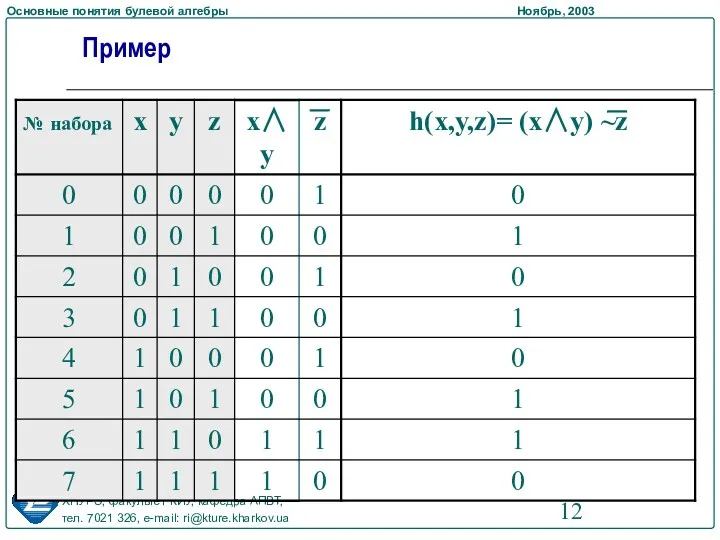
- 12. Пример
- 13. Time-Out
- 14. Законы и тождества алгебры логики. 1
- 15. Законы и тождества алгебры логики Связь эквивалентности ~ с дизъюнкцией, конъюнкцией и отрицанием: x~y=xy ∨ x
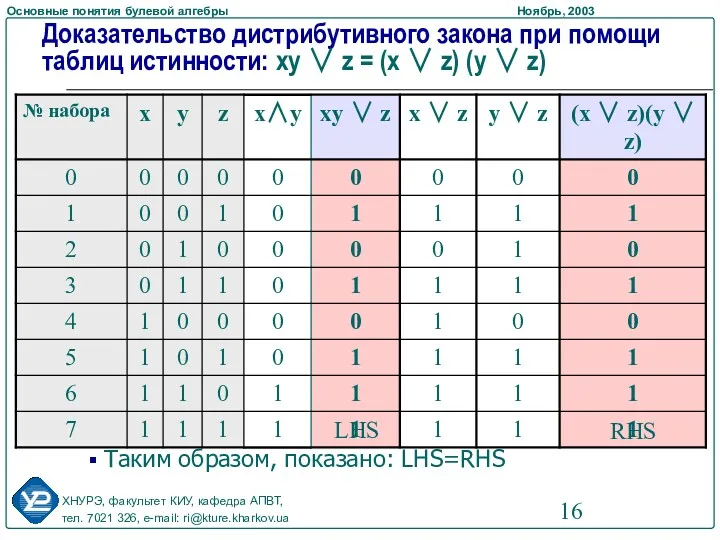
- 16. Доказательство дистрибутивного закона при помощи таблиц истинности: xy ∨ z = (x ∨ z) (y ∨
- 17. ДНФ и КНФ
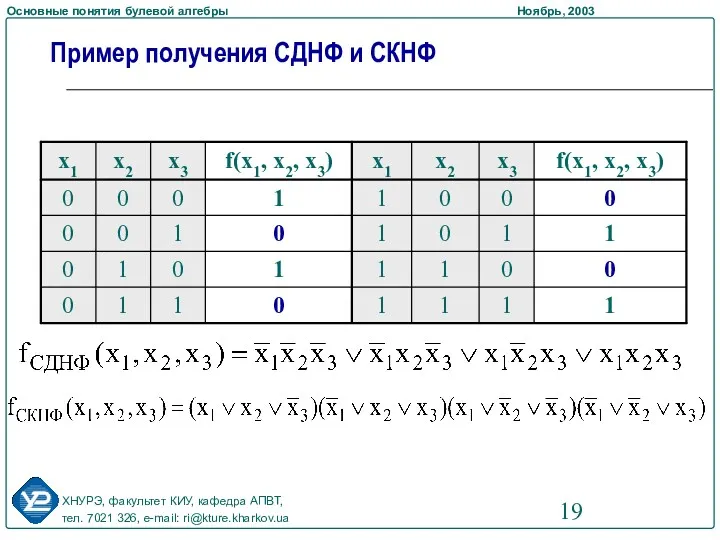
- 18. Def: Совершенной ДНФ (СДНФ) называется ДНФ, в которой нет равных элементарных конъюнкций и все элементарные конъюнкции
- 19. Пример получения СДНФ и СКНФ
- 20. Теорема Шеннона Любая булева функция f≠0 представима в виде разложения Шеннона: Следствие Предельное разложение Шеннона (k=n)
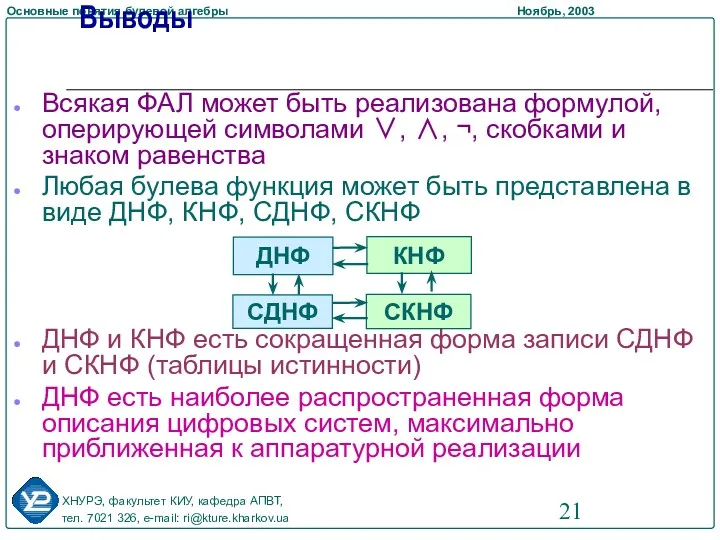
- 21. Выводы Всякая ФАЛ может быть реализована формулой, оперирующей символами ∨, ∧, ¬, скобками и знаком равенства
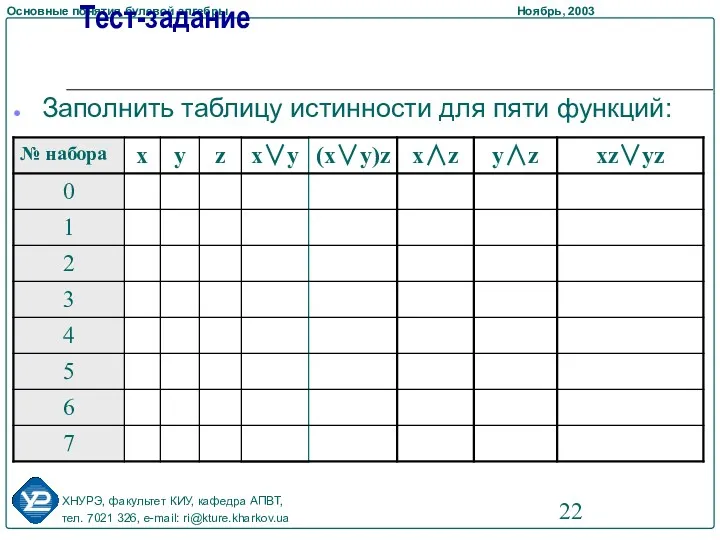
- 22. Тест-задание Заполнить таблицу истинности для пяти функций:
- 24. Скачать презентацию













 Презентация для викторины по геометрии 4 класс
Презентация для викторины по геометрии 4 класс Виды стохастических задач на уроках математики
Виды стохастических задач на уроках математики Алгоритм сложения трёхзначных чисел
Алгоритм сложения трёхзначных чисел Построение графика квадратичной функции
Построение графика квадратичной функции Элементы алгебры логики. Математические основы информатики. Таблицы истинности
Элементы алгебры логики. Математические основы информатики. Таблицы истинности Величины.
Величины. Презентация к уроку по математике для 2 класса. Тема:Чтение и запись трехзначных чисел. Решение задач.
Презентация к уроку по математике для 2 класса. Тема:Чтение и запись трехзначных чисел. Решение задач. Основные понятия в области метрологии
Основные понятия в области метрологии 1,2,3,4,5 ...
1,2,3,4,5 ... Высшая математика. Вебинар для студентов заочной формы обучения (дистанционная)
Высшая математика. Вебинар для студентов заочной формы обучения (дистанционная) Деление обыкновенных дробей. Устная работа
Деление обыкновенных дробей. Устная работа Теорема о площади треугольника
Теорема о площади треугольника Число 0.
Число 0. Масштаб. 6 класс
Масштаб. 6 класс Алгебраическая сумма и её свойства
Алгебраическая сумма и её свойства Арифметикалық және геометриялық прогрессияларды есептер шығаруда қолдану
Арифметикалық және геометриялық прогрессияларды есептер шығаруда қолдану Свойства степени с рациональным показателем
Свойства степени с рациональным показателем Урок математики в 3 классе (урок с применением ЭОР)
Урок математики в 3 классе (урок с применением ЭОР) Основные понятия и термины метрологии
Основные понятия и термины метрологии Угол между плоскостями
Угол между плоскостями Веселый счет
Веселый счет Действия с дробями. Задание для устного счета. Упражнение 15. 6 класс
Действия с дробями. Задание для устного счета. Упражнение 15. 6 класс Подобие. Подобные треугольники
Подобие. Подобные треугольники Множества. Эквивалентные множества
Множества. Эквивалентные множества Дисперсия и ее свойства
Дисперсия и ее свойства Замечательные точки треугольника. 8 класс
Замечательные точки треугольника. 8 класс Все действия с дробями. Урок математики в 5 классе
Все действия с дробями. Урок математики в 5 классе Сложение и вычитание векторов
Сложение и вычитание векторов