Содержание
- 2. Общий вид СНУ где F – функции нескольких переменных, х – неизвестные n –порядок системы
- 3. Методы решения СНУ: 1. Прямых методов для решения СНУ не существует. 2. Итерационные методы. Методы являются
- 4. Метод Зейделя (метод простых итераций) Ограниченный круг СНУ Исходные данные: Fi(x1, x2,…, xn) Х(0) Е
- 5. Требование Функции Fi(x1, x2,…, xn) должны быть непрерывны в окрестности точки истинного решения Х и точки
- 6. Метод Зейделя на примере СНУ 3-го порядка Из 1-го уравнения выражаем неизвестное х1. Из 2-го уравнения
- 7. Получим новую систему: 2. В правую часть 1-го уравнения подставляем начальные приближения неизвестных х2(0) и х3(0).
- 8. 5. Далее рассчитывается разность между значениями начальных приближений и уточненными значениями неизвестных. Если то считается, что
- 9. ЗАМЕЧАНИЕ Метод Зейделя применим, если неизвестные из соответствующих уравнений можно выразить в явном виде. Метод Зейделя
- 10. Примеры:
- 11. Метод Ньютона для решения СНУ Основа: разложение функций в ряд Тейлора относительно значений начальных приближений неизвестных.
- 12. Для реализации метода Ньютона необходимо задать следующие данные: 1. Выражения для функций F1, F2 ,…, Fn
- 13. Требование Функции Fi(x1, x2,…, xn) должны быть непрерывны и дифференцируемы в окрестности точки истинного решения Х
- 14. Метод Ньютона на примере СНУ 3-го порядка Задано: x10, x20 и x30. Истинное решение системы: x1,
- 15. F1, F2 и F3 разлагаются в ряд Тейлора. Члены, содержащие производные старше первого порядка отбрасываются. Преобразуем
- 16. Получим систему линейных алгебраических уравнений: Неизвестные - Δx1, Δx2 и Δx3, Вектор-столбец свободных членов – F1,
- 17. СЛАУ решается любым известным методом (метод Гаусса, метод Крамера), получаем значения неизвестных Δx1, Δx2 и Δx3
- 18. Если полученные значения Δx1 и Δx2 и Δx3 по модулю оказались менее заданной точности Е, то
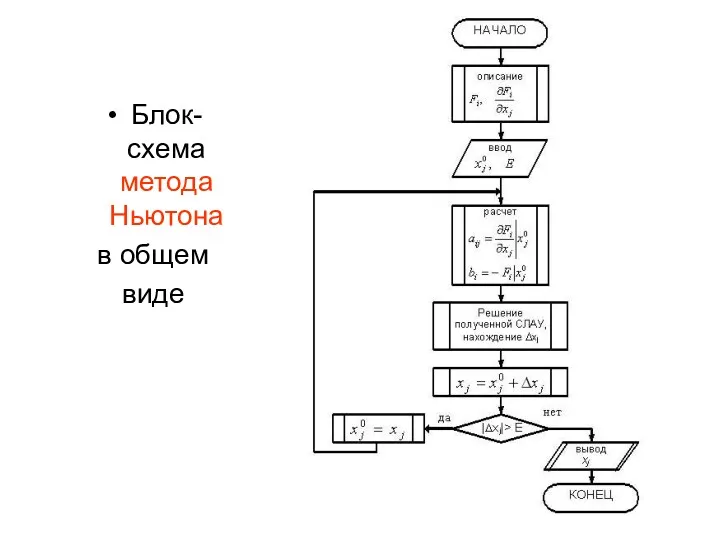
- 19. Блок-схема метода Ньютона в общем виде
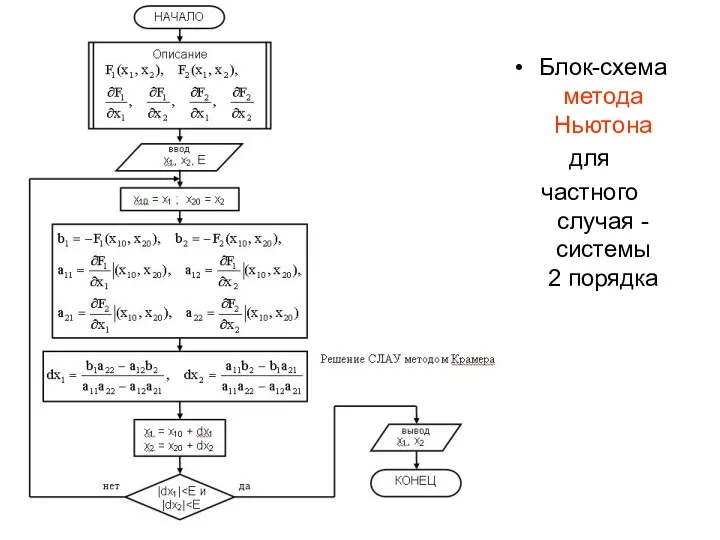
- 20. Блок-схема метода Ньютона для частного случая - системы 2 порядка
- 22. Скачать презентацию

















 Устный счет
Устный счет Координатна пряма. Поняття
Координатна пряма. Поняття Округление чисел. Чем похожи числа?
Округление чисел. Чем похожи числа? Математика. Решение задач
Математика. Решение задач Путешествие в мир математики
Путешествие в мир математики Решение обыкновенных дифференциальных уравнений
Решение обыкновенных дифференциальных уравнений Математика. 1 класс. Урок 73. Длина. Сантиметр - Презентация
Математика. 1 класс. Урок 73. Длина. Сантиметр - Презентация Системы линейных уравнений
Системы линейных уравнений Приближение десятичных дробей. 6 класс
Приближение десятичных дробей. 6 класс Решение уравнений. 5 класс
Решение уравнений. 5 класс Случайные величины. Определение случайной величины (лекция 6)
Случайные величины. Определение случайной величины (лекция 6) Математические основы анализа свойств систем и наблюдения их состояния (лекция № 17)
Математические основы анализа свойств систем и наблюдения их состояния (лекция № 17) Средняя линия треугольника
Средняя линия треугольника Задачи по математике
Задачи по математике презентация к пресс-конференции Великие математики
презентация к пресс-конференции Великие математики Развитие устных вычислительных навыков
Развитие устных вычислительных навыков Вычитание числа с переходом через десяток, вида 13-
Вычитание числа с переходом через десяток, вида 13- Математика в различных сферах жизнедеятельности
Математика в различных сферах жизнедеятельности Призма және оның элементтері
Призма және оның элементтері Теорема Пифагора
Теорема Пифагора Проект Математика вокруг нас. Числа в загадках, пословицах и поговорках. Обобщение опыта освоения новых форм работы, применения новой технологии позволит педагогу повысить эффективность образовательной системы
Проект Математика вокруг нас. Числа в загадках, пословицах и поговорках. Обобщение опыта освоения новых форм работы, применения новой технологии позволит педагогу повысить эффективность образовательной системы Смешанные числа
Смешанные числа Отношения и пропорции
Отношения и пропорции Конспект урока по математике по теме Таблица умножения. Закрепление. Решение задач+презентация
Конспект урока по математике по теме Таблица умножения. Закрепление. Решение задач+презентация Формирование познавательных ууд на уроках математики в начальной школе.
Формирование познавательных ууд на уроках математики в начальной школе. Понятие и значение статистического наблюдения
Понятие и значение статистического наблюдения Тренажёр табличное умножение
Тренажёр табличное умножение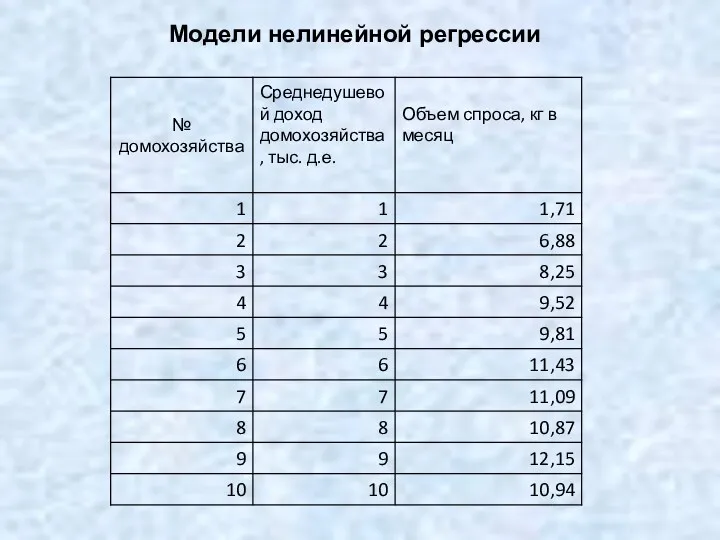 Модель парной нелинейной регрессии
Модель парной нелинейной регрессии