Содержание
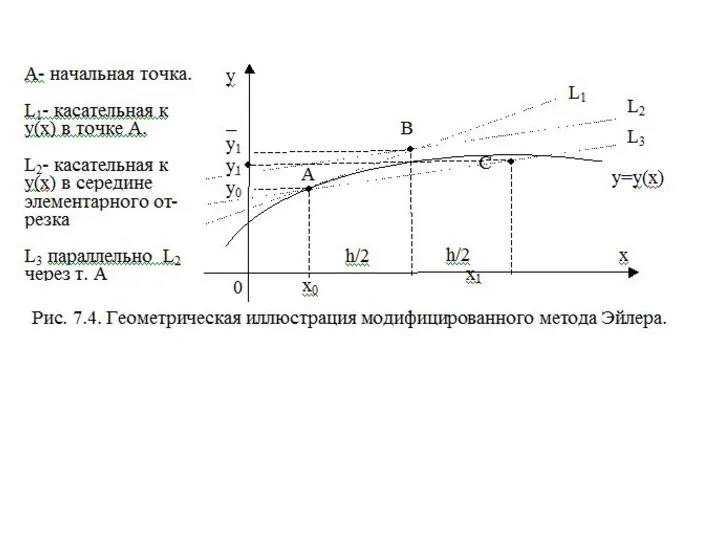
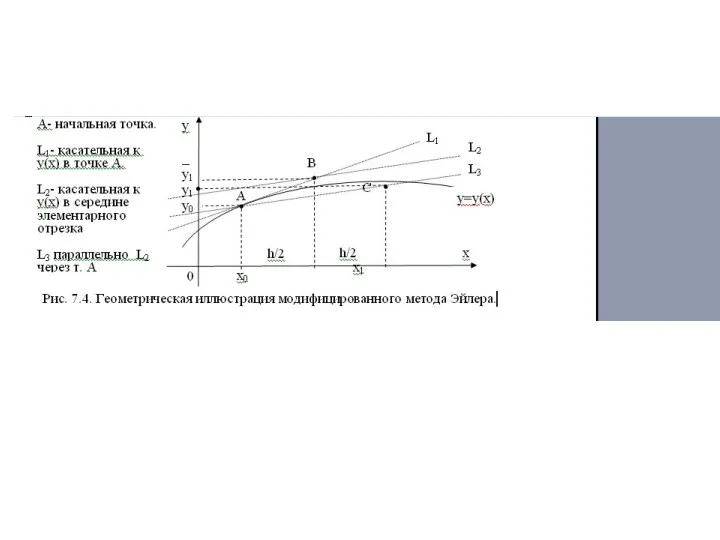
- 27. 7.2. Модифицированный метод Эйлера (метод Рунге-Кутта 2-го порядка). Для повышения точности формула Эйлера применяется дважды на
- 29. Расчётные формулы: - значение функции в середине отрезка [x0,x1]. - значение функции в конце отрезка [x0,x1].
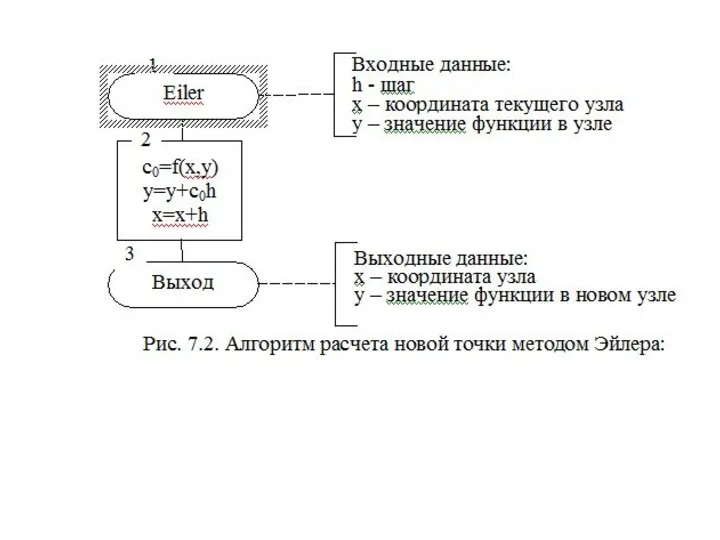
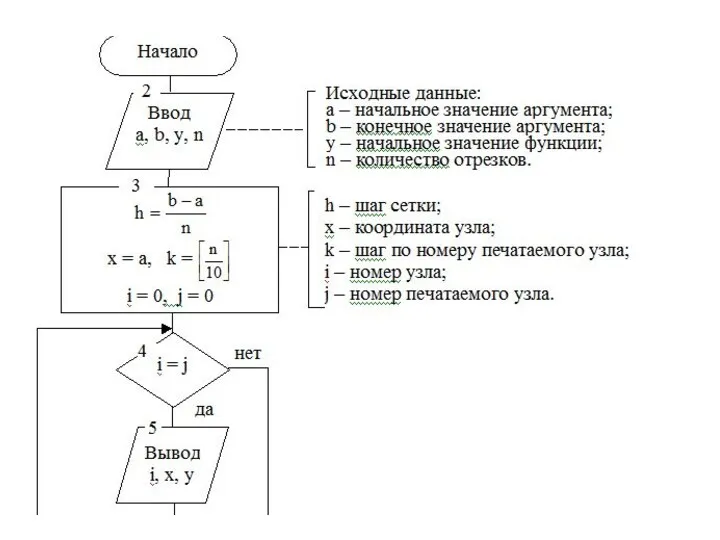
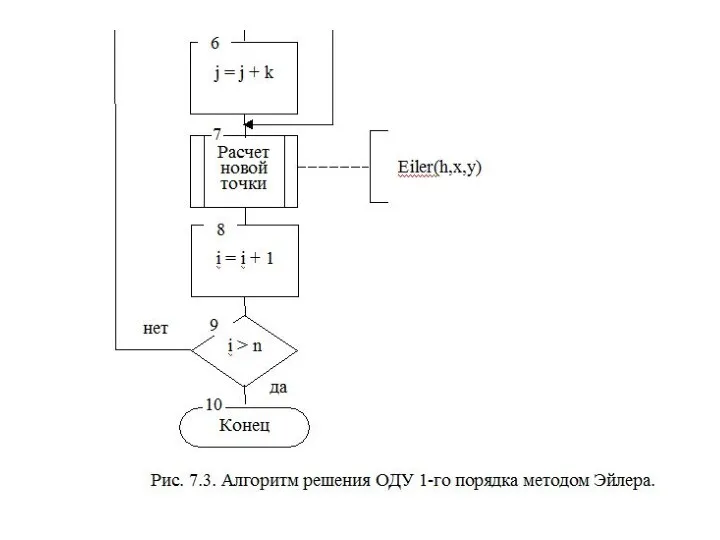
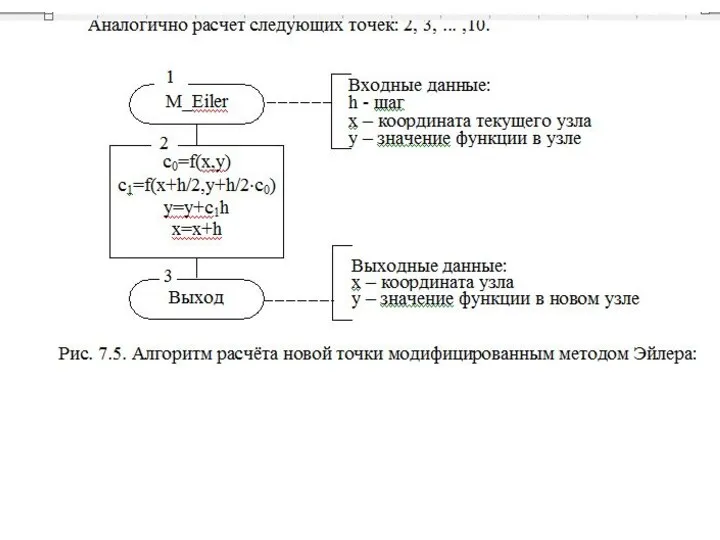
- 30. Алгоритм решения ОДУ отличается от описанного ранее алгоритма метода Эйлера (рис 7.3) только алгоритмом расчета новой
- 31. Пример 7.2. Решение ранее рассмотренного уравнения (пример 7.1) модифицированным методом Эйлера. y’ - 2⋅y + x2
- 32. Расчёт первой точки. Аналогично расчёт следующих точек: 2, 3, ... ,10.
- 34. Скачать презентацию



















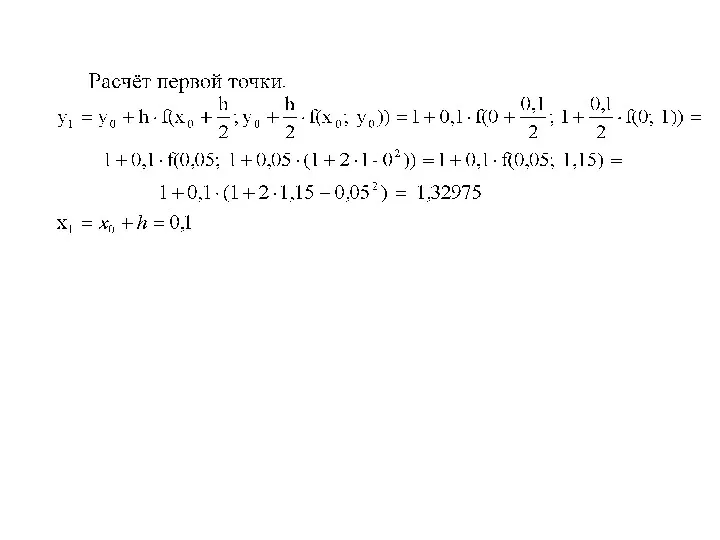

![Расчётные формулы: - значение функции в середине отрезка [x0,x1]. -](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/296813/slide-28.jpg)



 Интеллектуальная игра: Морской бой
Интеллектуальная игра: Морской бой Размещения, сочетания, перестановки. 11 класс
Размещения, сочетания, перестановки. 11 класс Натуральні числа і дії з ними. Геометричні фігури і величини
Натуральні числа і дії з ними. Геометричні фігури і величини Математическое обеспечение САПР. Основные понятия и определения
Математическое обеспечение САПР. Основные понятия и определения Примитивно-рекурсивные операторы. Частично-рекурсивные функции
Примитивно-рекурсивные операторы. Частично-рекурсивные функции Дисперсия числового набора. 8 класс
Дисперсия числового набора. 8 класс Основы теории вероятностей
Основы теории вероятностей Вычитание рациональных чисел. 6 класс
Вычитание рациональных чисел. 6 класс Сфера. Уравнение сферы
Сфера. Уравнение сферы Деление многозначного на трёхзначное.
Деление многозначного на трёхзначное. Подготовка к введению задач в 2 действия
Подготовка к введению задач в 2 действия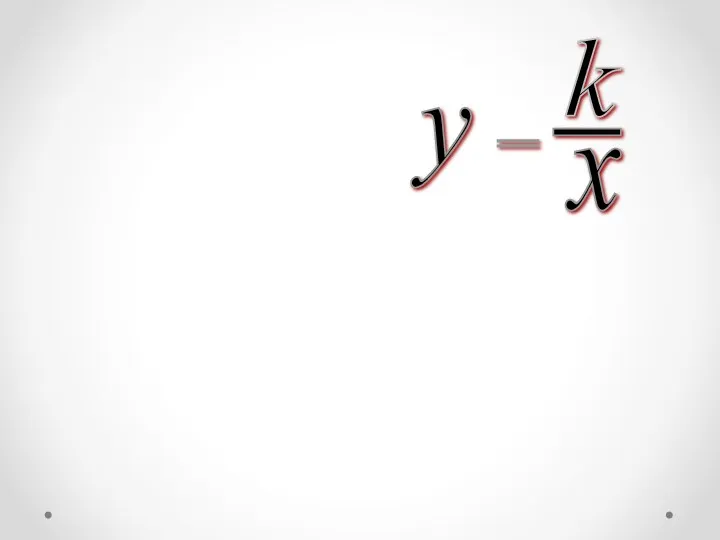 Функция обратной пропорциональности и её график
Функция обратной пропорциональности и её график Многогранники
Многогранники Математический досуг
Математический досуг Устный счёт 2 класс
Устный счёт 2 класс Сумма первых n-членов арифметической прогрессии
Сумма первых n-членов арифметической прогрессии Случаи сложения вида +4
Случаи сложения вида +4 Решение задач с помощью уравнений
Решение задач с помощью уравнений Презентация по математике Знакомство с умножением, 2 класс
Презентация по математике Знакомство с умножением, 2 класс Задачи на проценты: научился решать сам, научи друга. Практико–ориентированный проект
Задачи на проценты: научился решать сам, научи друга. Практико–ориентированный проект Задачи на сложение и вычитание десятичных дробей
Задачи на сложение и вычитание десятичных дробей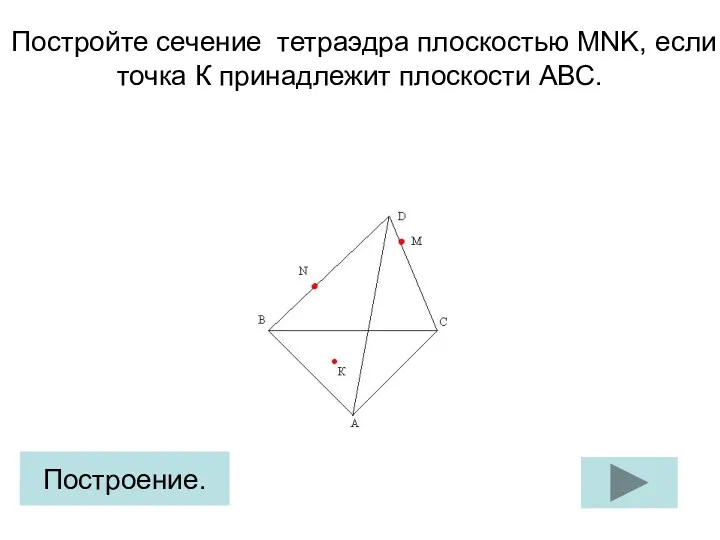 Тетраэдр. Построение сечения (задание 5)
Тетраэдр. Построение сечения (задание 5) Аксонометрические построения. (Лекция 7)
Аксонометрические построения. (Лекция 7) Практикум № 7 по решению стереометрических задач
Практикум № 7 по решению стереометрических задач Решение квадратных уравнений. Урок обобщения и систематизации знаний
Решение квадратных уравнений. Урок обобщения и систематизации знаний Решение задач на перпендикулярность прямой и плоскости. (10 класс)
Решение задач на перпендикулярность прямой и плоскости. (10 класс) Методика формирования навыков устного счета на уроках математики у обучающихся с нарушением интеллектуального развития
Методика формирования навыков устного счета на уроках математики у обучающихся с нарушением интеллектуального развития Презентация к уроку математики в 1 классе Треугольник
Презентация к уроку математики в 1 классе Треугольник