Содержание
- 2. Пусть даны две переменные x и y с областями изменения X и Y. Предположим, что переменной
- 3. Определение понятия функции Можно в определении понятия функции стать на более общую точку зрения, допуская, чтобы
- 4. Основные ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ линейная функция y=kx+b показательная (0 логарифмическая x (0 степенная y=xⁿ; тригонометрические sin x,
- 5. Пример 1.1. Найти область определения функции Решение. Известно, что корень четной степени определен только при неотрицательном
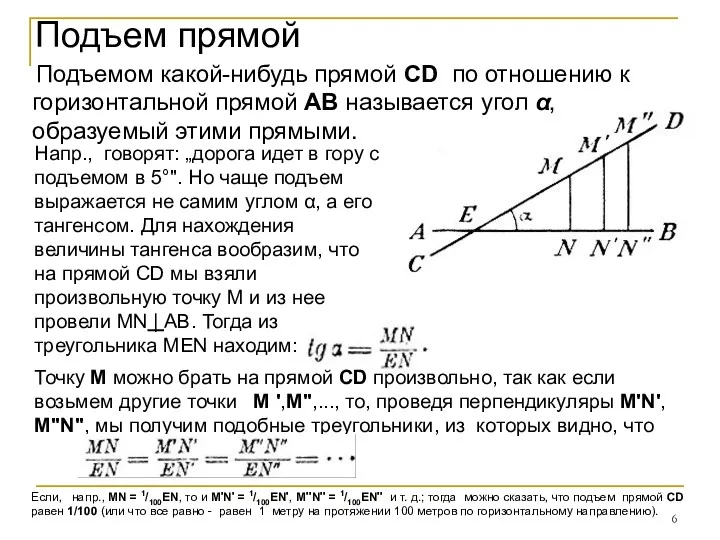
- 6. Подъем прямой Подъемом какой-нибудь прямой CD по отношению к горизонтальной прямой АВ называется угол α, образуемый
- 7. Уклон этот тоже измеряется чаще всего тангенсом угла α , образованного CD с AВ, так что
- 8. Для этого возьмем две какие-нибудь точки на прямой CD , напр.. М и M', проведем их
- 9. Общее определение касательной к кривой Если допустим, что точка В приближается к А неограниченно близко, то
- 10. Вспомним, что когда в геометрии говорилось о касательной к окружности, то там она определялась как такая
- 11. подъем
- 12. Определение производной как предела отношения приращений Предел этого среднего подъема, когда Δх —> 0, есть подъем
- 13. Пример вычисления производной по определению f‛ Решение
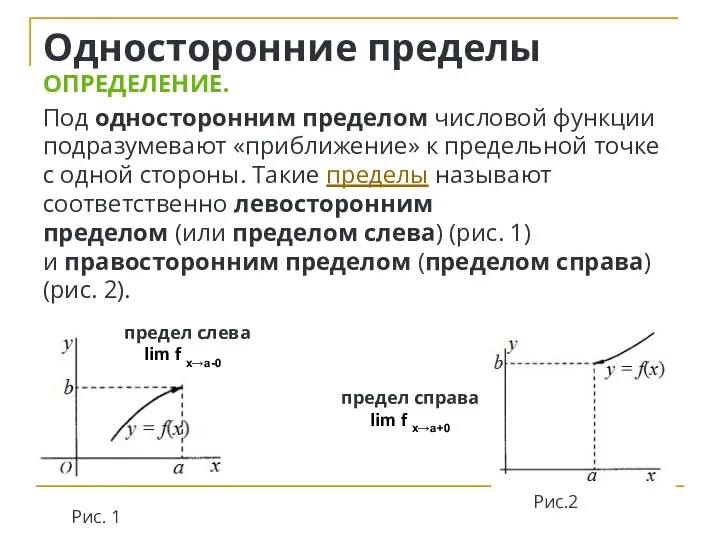
- 14. Односторонние пределы ОПРЕДЕЛЕНИЕ. Под односторонним пределом числовой функции подразумевают «приближение» к предельной точке с одной стороны.
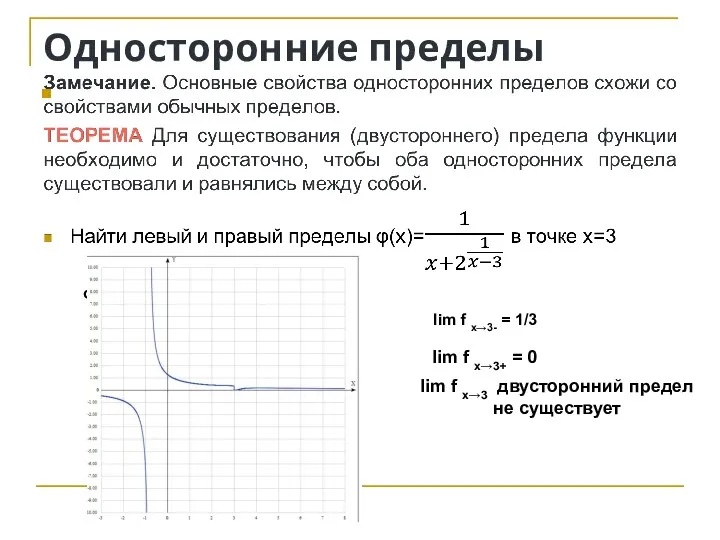
- 15. Односторонние пределы lim f x→3 двусторонний предел не существует
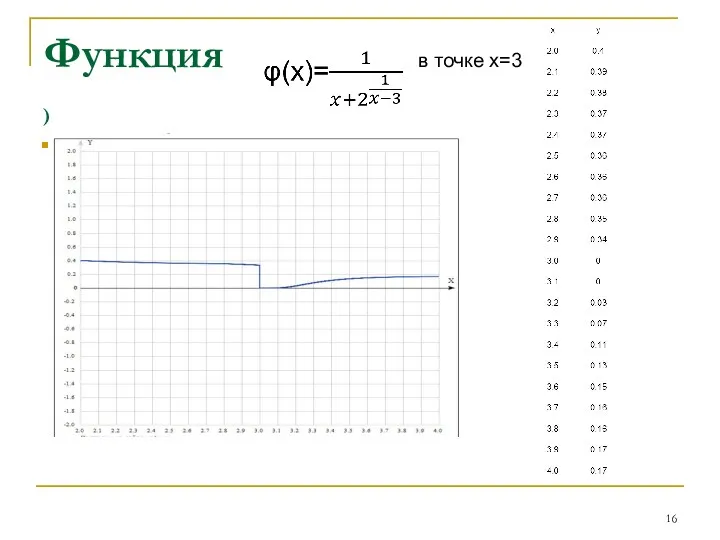
- 16. Функция в точке х=3 ) в точке х=3
- 17. Производная от функции у = ах2 Эта функция геометрически выражается параболой. Чтобы найти подъем этой параболы
- 18. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ Функция, имеющая производную в некоторой точке, называется дифференцируемой в этой точке. Операция нахождения производной
- 19. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ Функции одного переменного. При нахождении производных применяются правила дифференцирования: (2.1) (2.2) (2.3) (2.4)
- 20. Сложная функция Опред. Если у зависит от х через посредство промежуточного аргумента u, то у называется
- 21. Найти производную функции по определенпю y=sinx
- 22. Таблица основных производных
- 23. сайт для заочников http://www.mathprofi.ru/proizvodnaya_slozhnoi_funkcii.html
- 24. Пример 2.1. Найти производную функции Решение. Применим формулы (2.4), (2.1) и (дважды) формулу производной степенной функции:
- 25. Пример 2.2. Найти производную функции Решение. Сначала воспользуемся формулой (2.2) и табличной производной косинуса для сложной
- 26. Пример 2.3. Найти в точке производную функции Решение. Предварительно «подготовим» функцию к дифференцированию Теперь воспользуемся формулами
- 27. Подставляем значение и получаем:
- 28. Пример 2.4. Для найти вторую производную ( ). Решение. Сначала найдем первую производную: Далее воспользуемся тем,
- 29. Найти производные функций
- 30. ЭЛЕМЕНТЫ ТЕОРИИ ОПТИМИЗАЦИИ ЭКСТРЕМУМЫ функции одного переменного Пусть D(f) – область определения функции и Если для
- 31. При поиске экстремумов и точек экстремума функции придерживаются следующей схемы рассуждений. 1) Установить область определения функции
- 32. При поиске экстремумов и точек экстремума функции придерживаются следующей схемы рассуждений. 5) Проверить достаточное условие экстремума:
- 33. Пример 8.2. Найти экстремумы функции Данная функция определена для всех действительных чисел, ее производная имеет вид
- 34. Наибольшее и наименьшее значение функции одного переменного на числовом интервале Теорема 8.1. Если функция определена и
- 35. Теорема 8.1 позволяет построить алгоритм решения задачи на поиск наибольшего и наименьшего значения функции , определенной
- 36. Найти наибольшее и наименьшее значения функции у=х3-2х2+х-2 на заданном отрезке [0,5;2].
- 37. Асимптоты
- 38. Найти асимптоты функции у=1/(х-2)
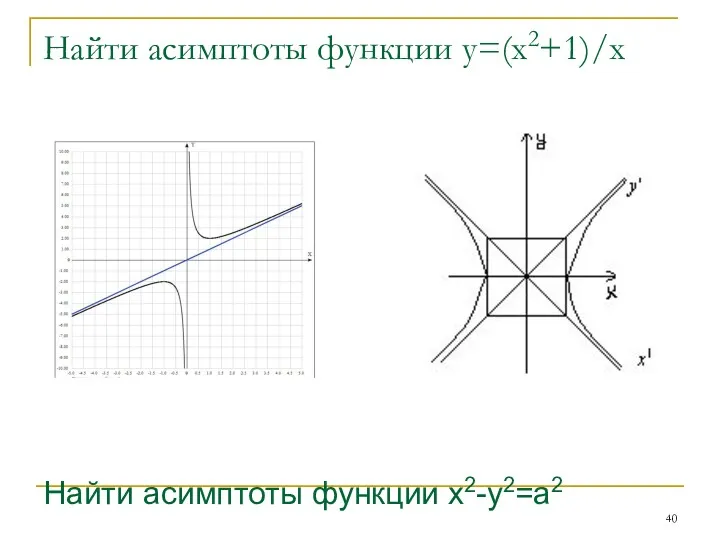
- 39. Найти асимптоты функции у=(х2+1)/х Найти асимптоты функции x2-y2=a2
- 40. Найти асимптоты функции у=(х2+1)/х Найти асимптоты функции x2-y2=a2
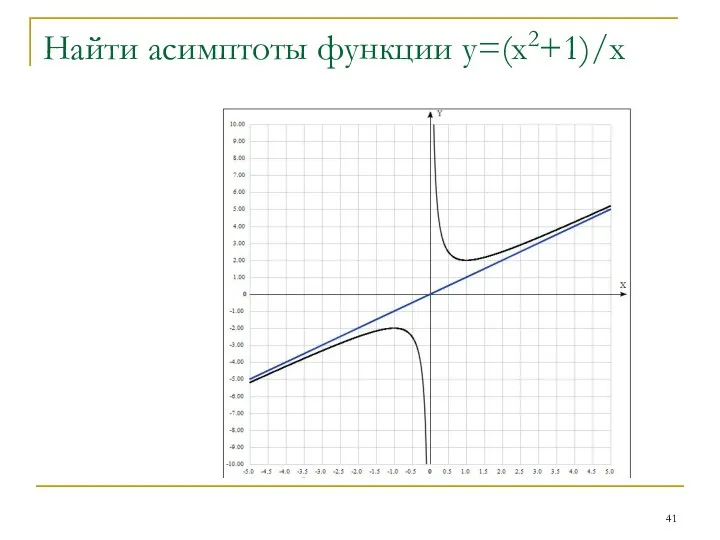
- 41. Найти асимптоты функции у=(х2+1)/х
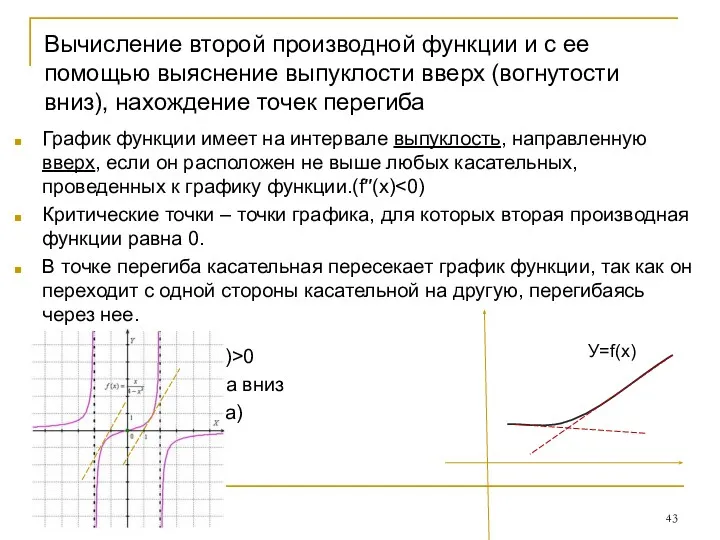
- 43. Вычисление второй производной функции и с ее помощью выяснение выпуклости вверх (вогнутости вниз), нахождение точек перегиба
- 44. Исследование функции производится по схеме: 1) Область определения. 2) Область значений функции. 3) Нули функции. 4)
- 45. max min
- 46. y y′′ x -1 - +
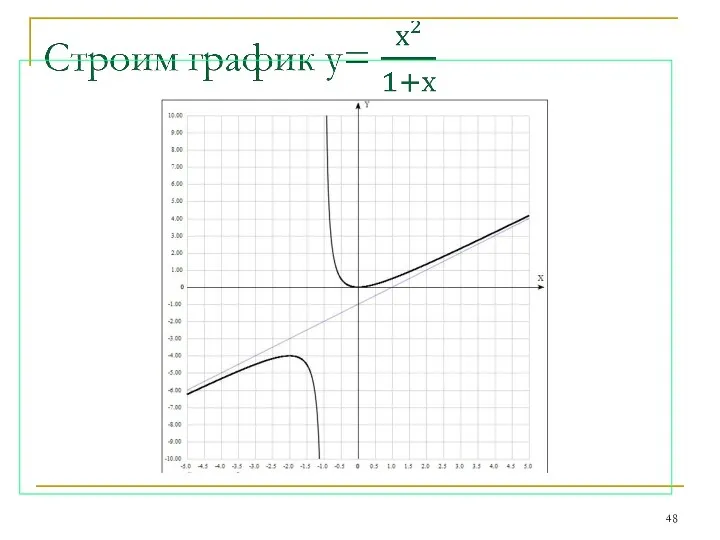
- 47. 7) Ищем наклонную асимптоту: k= y y′′ x -1 - + Итак, у=kx+b=х-1 наклонная асимптота
- 49. Дз:
- 51. Скачать презентацию






























![Найти наибольшее и наименьшее значения функции у=х3-2х2+х-2 на заданном отрезке [0,5;2].](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/296812/slide-35.jpg)









 ОГЭ 2020-21. Задание №14. Арифметическая прогрессия
ОГЭ 2020-21. Задание №14. Арифметическая прогрессия Линейное уравнение с одной переменной. Что называется уравнением?
Линейное уравнение с одной переменной. Что называется уравнением? График функции
График функции Десятичные дроби : сложение , вычитание , сравнение, округление, умножение на натуральное число
Десятичные дроби : сложение , вычитание , сравнение, округление, умножение на натуральное число Центральная симметрия
Центральная симметрия урок математики 1класс Число и цифра 10
урок математики 1класс Число и цифра 10 Математический кружок. Занятие 3. Инварианты
Математический кружок. Занятие 3. Инварианты Теорема Виета
Теорема Виета Информатика в задачах теплоэнергетики
Информатика в задачах теплоэнергетики Понятие многогранника, призмы и их элементов
Понятие многогранника, призмы и их элементов Игра Счастливый случай. Общие вопросы по математике (5 класс)
Игра Счастливый случай. Общие вопросы по математике (5 класс) XIX ғасырдағы математиканың алпауыттары
XIX ғасырдағы математиканың алпауыттары Урок математики
Урок математики Математика Путешествие к Робинзону Крузо
Математика Путешествие к Робинзону Крузо Неопределенный и определенный интеграл
Неопределенный и определенный интеграл Вводное повторение. Геометрия 9 класс
Вводное повторение. Геометрия 9 класс Деление с остатком
Деление с остатком Арифметическая прогрессия. 9 класс
Арифметическая прогрессия. 9 класс Презентация к уроку математики в 4 классе.
Презентация к уроку математики в 4 классе. Прямокутна система координат
Прямокутна система координат Комбинаторные задачи. Комбинаторика
Комбинаторные задачи. Комбинаторика Задачи по теме Призма и пирамида
Задачи по теме Призма и пирамида Математическая раскраска
Математическая раскраска Столбчатые диаграммы, графики. Задание 8, ОГЭ
Столбчатые диаграммы, графики. Задание 8, ОГЭ Преобразование графиков тригонометрических функций
Преобразование графиков тригонометрических функций Обобщающий урок по теме: Признаки равенства треугольников
Обобщающий урок по теме: Признаки равенства треугольников Умножение дробей. Нахождение дроби от числа. 6 класс
Умножение дробей. Нахождение дроби от числа. 6 класс Неравенства. Знаки < , >
Неравенства. Знаки < , >