Содержание
- 2. Интерполяция Слово интерполяция (interpolatio) переводится с латинского, как изменение или обновление. С точки зрения математики, это
- 3. Интерполяция Если задана функция y(x), то это означает, что любому допустимому значению х сопоставлено значение y.
- 4. интерполяция При интерполировании рассматриваются три основные проблемы: выбор интерполяционной функции y(x); оценка погрешности интерполяции R(x); размещение
- 5. Интерполяция
- 6. Интерполяция Практически все интерполяционные методы базирующиеся на использовании в качестве интерполяционной функции полиномов, дают одни и
- 7. Интерполяция Следует отметить, что существует очевидный способ построения интерполяционной функции: из условия прохождения функции через все
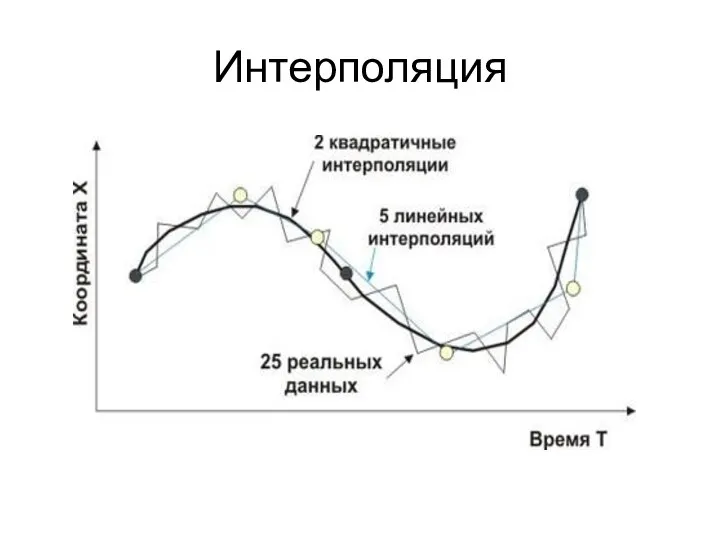
- 8. Локальная интерполяция Кусочно-постоянная интерполяция. На каждом локальном отрезке [xi–1, xi], i = 1, 2,…, N, интерполирующая
- 9. Кусочно-постоянная интерполяция При кусочно-постоянной интерполяции интерполяционный многочлен на каждом отрезке равен константе, а именно, левому или
- 10. Кусочно-постоянная интерполяция
- 11. Локальная интерполяция Кусочно-линейная интерполяция. На каждом интервале [xi–1, xi] функция является линейной Fi(z) = kiz+li. Значения
- 12. Кусочно-линейная интерполяция если Т.е. При использовании линейной интерполяции сначала нужно определить интервал, в который попадает искомое
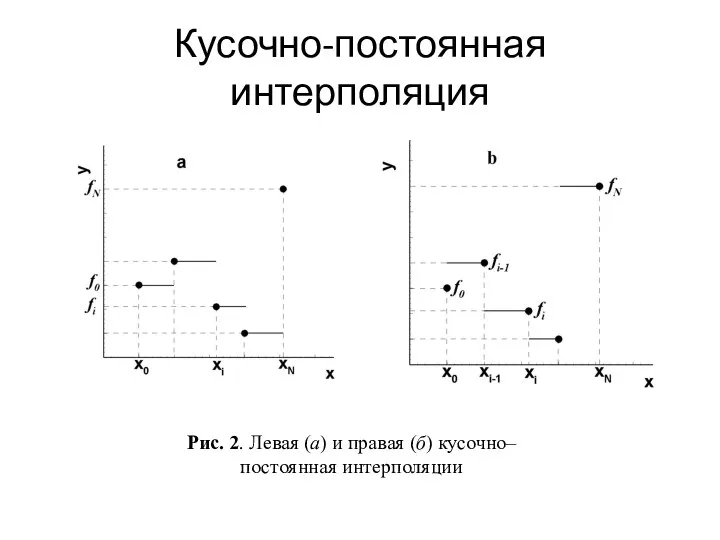
- 13. Локальная интерполяция Рис. 1. Левая кусочно-постоянная (а) и кусочно-линейная (б) интерполяции
- 14. Пример вычисления кусочно-постоянной и кусочно-линейной интерполяции
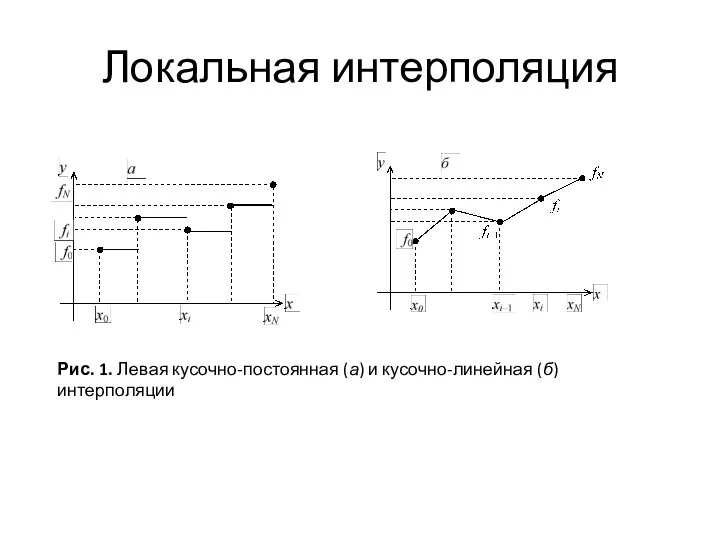
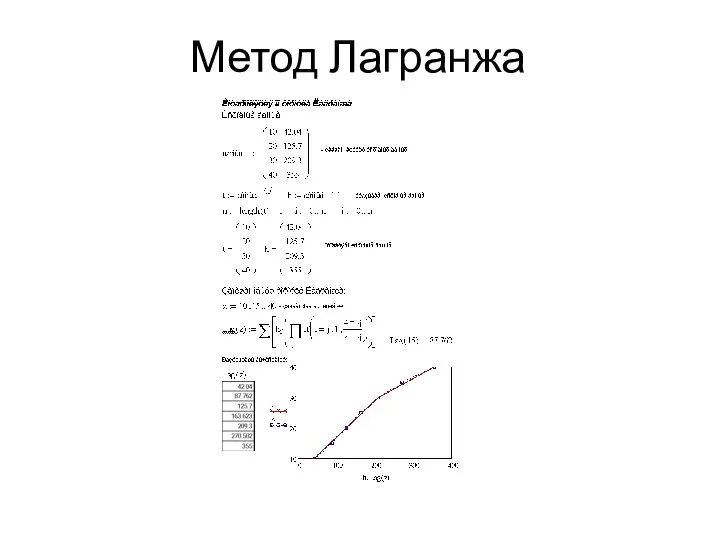
- 15. Метод Лагранжа ЛАГРАНЖ, ЖОЗЕФ ЛУИ (Lagrange, Joseph Louis) (1736–1813) (рис.1.2), французский математик и механик. Родился 25
- 16. Метод Лагранжа Пусть известны значения некоторой функции f(х) в n+1 различных произвольных точках yi=f(xi), i=0,…n. Для
- 17. Метод Лагранжа Если раскрыть произведение всех скобок в числителе, то получим полином n-го порядка от х,
- 18. Метод Лагранжа Дана таблично заданная функция (табл. 1.1.). Требуется найти h(t) при t=15оС. В нашем случае
- 19. Метод Лагранжа Решение: Запишем функцию Лагранжа в развернутом виде:
- 20. Метод Лагранжа Попробуем найти значение функции h(t) при t=15оС при n=2. Для интерполяции выберем точки 0,
- 21. Метод Лагранжа
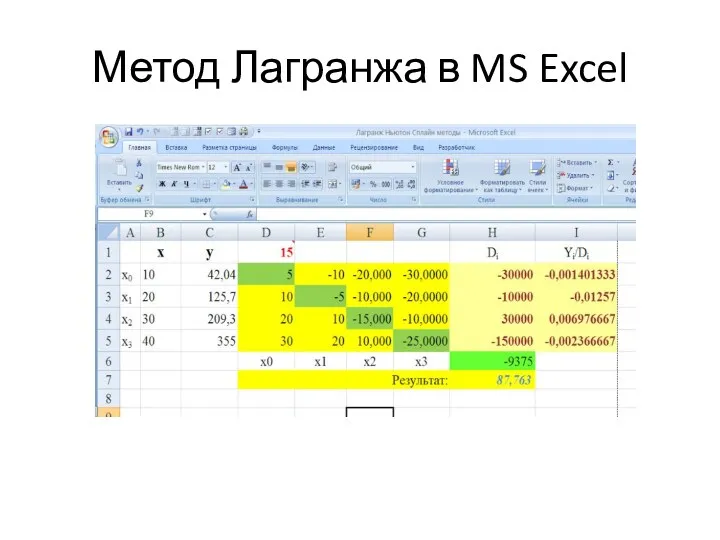
- 22. Метод Лагранжа в MS Excel
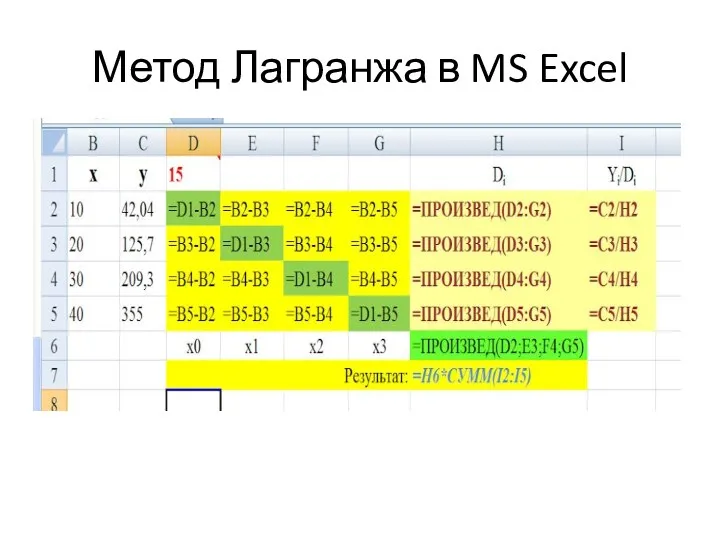
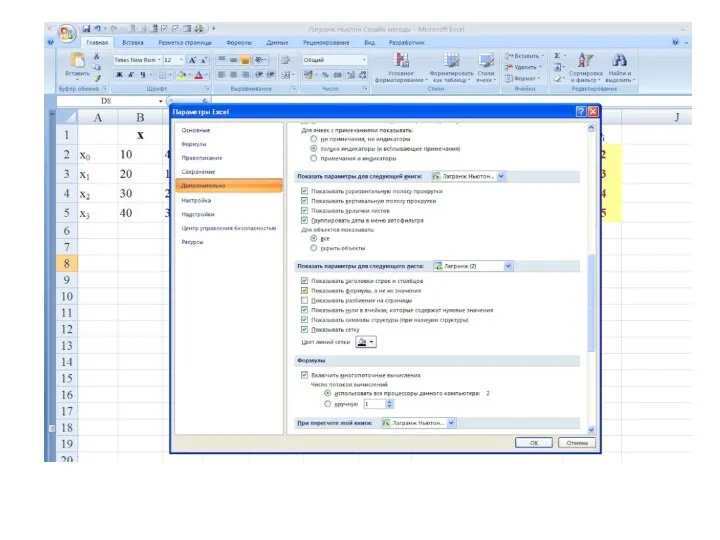
- 23. Метод Лагранжа в MS Excel
- 25. Метод Ньютона Английский математик, физик, алхимик и историк Исаак Ньютон родился в местечке Вулсторп в Линкольншире
- 26. Метод Ньютона Интерполяция может производится для произвольно и равномерно расположенных узлов интерполяции Интерполяционный многочлен Ньютона записывается
- 27. Метод Ньютона Часто вводят безразмерную переменную q, показывающую сколько содержится шагов от x0 до заданной точки
- 28. Метод Ньютона Существует и вторая интерполяционная формула Ньютона (1687 год): Погрешность интерполяции можно оценить по выражению:
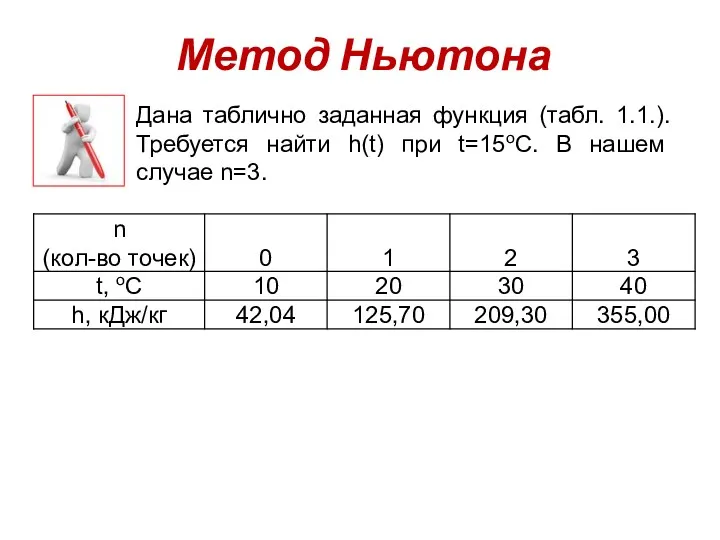
- 29. Дана таблично заданная функция (табл. 1.1.). Требуется найти h(t) при t=15оС. В нашем случае n=3. Метод
- 30. Метод Ньютона Для интерполяции будем использовать только первые три точки, а остальные для оценки погрешности. В
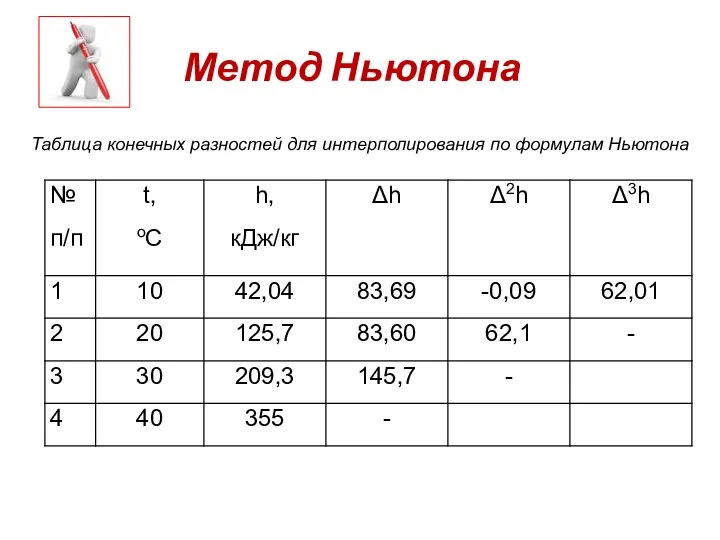
- 31. Метод Ньютона Таблица конечных разностей для интерполирования по формулам Ньютона
- 32. Метод Ньютона Подставляем все необходимые значения в формулу Ньютона из нашей таблицы (лист 19), получим:
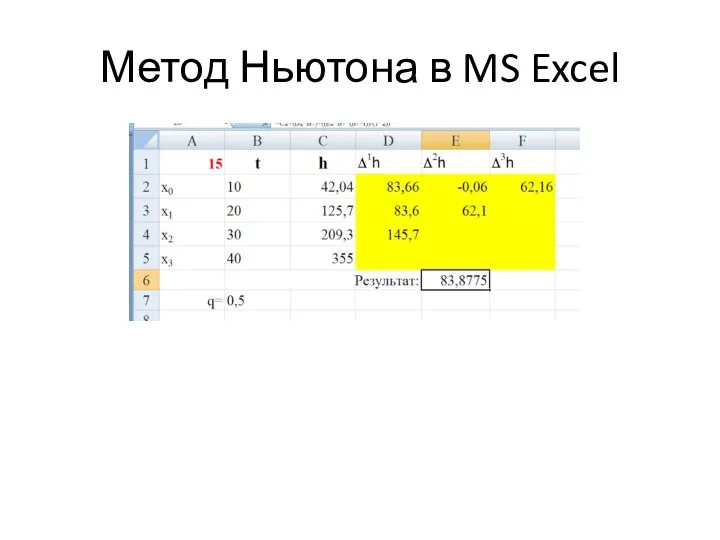
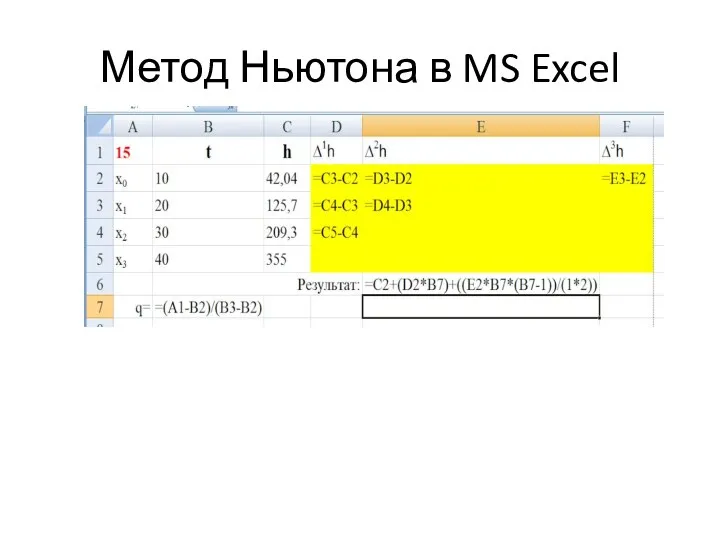
- 33. Метод Ньютона в MS Excel
- 34. Метод Ньютона в MS Excel
- 35. Пример Интерполирование по формулам Ньютона в программе Mathcad.
- 36. Метод сплайнов Слово сплайн, происходящее от английского слова spline, означает гибкую линейку, используемую для проведения гладких
- 37. Метод сплайнов На каждом отрезке [xi-1, xi], i=1,2,…N будем искать функцию S(x)= Si(x) в виде полинома
- 38. Метод сплайнов Неизвестные коэффициенты , находим из: условий интерполяции: непрерывности функции непрерывности первой и второй производной:
- 39. Метод сплайнов Для определения неизвестных получаем систему уравнений: , ; Недостающие два уравнения выводятся из дополнительных
- 40. Метод сплайнов Можно показать, что при этом . Из системы можно исключить неизвестные , получив систему
- 41. Метод сплайнов В случае постоянной сетки система уравнений упрощается:
- 42. Для вычисления значения в произвольной точке отрезка необходимо решить систему уравнений на коэффициенты сi, , затем
- 43. Метод сплайнов
- 44. Пример сплайн интерполяции ручной способ
- 45. Пример сплайн интерполяции
- 46. Пример сплайн интерполяции MS Excel
- 47. Интерполяция в MathCAD Функции интерполяции определяют кривую, точно проходящую через заданные точки. Из-за этого результат очень
- 49. Скачать презентацию





![Локальная интерполяция Кусочно-постоянная интерполяция. На каждом локальном отрезке [xi–1, xi],](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/443434/slide-7.jpg)

![Локальная интерполяция Кусочно-линейная интерполяция. На каждом интервале [xi–1, xi] функция](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/443434/slide-10.jpg)















![Метод сплайнов На каждом отрезке [xi-1, xi], i=1,2,…N будем искать](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/443434/slide-36.jpg)







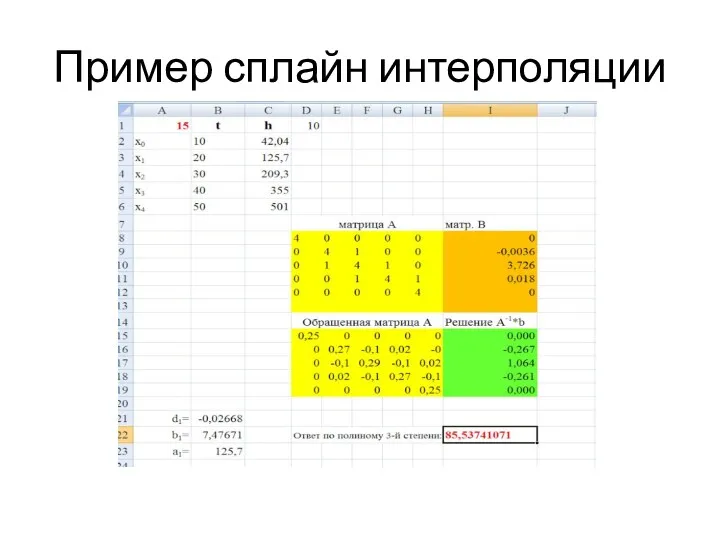
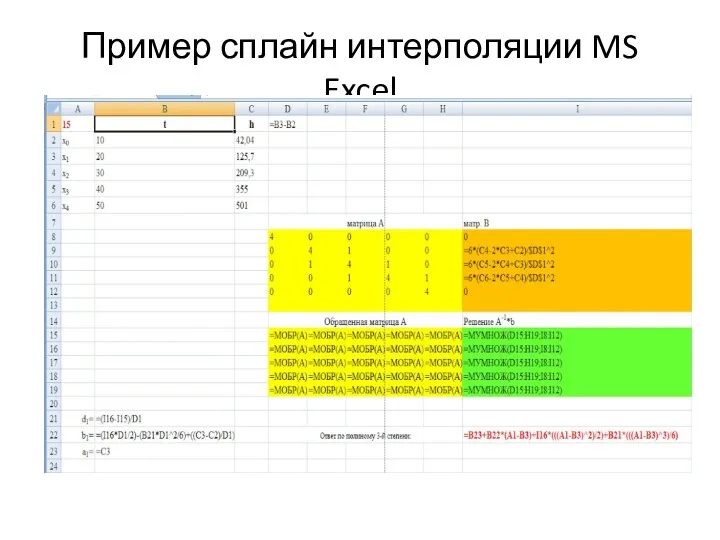

 Таблица сложения в пределах 20.
Таблица сложения в пределах 20. Деление многозначного на трёхзначное число. Решение задач.
Деление многозначного на трёхзначное число. Решение задач. Дифференцирование показательной и логарифмической функции. 11 класс
Дифференцирование показательной и логарифмической функции. 11 класс Углы и многоугольники. 5 класс
Углы и многоугольники. 5 класс Абсолютные и относительные статистические показатели
Абсолютные и относительные статистические показатели Система подготовки к ОГЭ и ЕГЭ по математике
Система подготовки к ОГЭ и ЕГЭ по математике Теория множеств
Теория множеств Экономические задачи. Подготовка к ОГЭ по математике
Экономические задачи. Подготовка к ОГЭ по математике Одночлены. Арифметические операции над одночленами
Одночлены. Арифметические операции над одночленами Логические законы и правила преобразования логических выражений
Логические законы и правила преобразования логических выражений Считаем и играем
Считаем и играем Формулы сокращенного умножения. Квадрат суммы
Формулы сокращенного умножения. Квадрат суммы Слайды к уроку математики в 1 классе.
Слайды к уроку математики в 1 классе. Масштаб. Практическое применение масштаба
Масштаб. Практическое применение масштаба Сбор и группировка статистических данных
Сбор и группировка статистических данных Неравенства с одной переменной
Неравенства с одной переменной Как построить график функции
Как построить график функции Приключение принцессы Софии
Приключение принцессы Софии Представьте числа в виде суммы разрядных слагаемых
Представьте числа в виде суммы разрядных слагаемых Решение задач на смеси и сплавы
Решение задач на смеси и сплавы Решение заданий В8 ЕГЭ по математике
Решение заданий В8 ЕГЭ по математике Двугранный угол
Двугранный угол Элементы комбинаторики
Элементы комбинаторики Основные теоремы о пределах. Способы вычисления пределов функций. (Семинар 5)
Основные теоремы о пределах. Способы вычисления пределов функций. (Семинар 5) Статистика бюджета. Экономические модели
Статистика бюджета. Экономические модели Читання і запис чисел. Додавання та віднімання 1. Задача, яка містить два запитання
Читання і запис чисел. Додавання та віднімання 1. Задача, яка містить два запитання Методика навчання нумерації в межах 1000 та багатоцифрових чисел (7 клас)
Методика навчання нумерації в межах 1000 та багатоцифрових чисел (7 клас) Определение многогранника
Определение многогранника