Содержание
- 2. Понятие множества Под множеством понимается некоторая, вполне определенная совокупность объектов или элементов. Георг Кант: объединение в
- 3. Определение Если a есть один из объектов множества А, то a есть элемент А, или принадлежит
- 4. Определение Пусть А и В – некоторые множества. А равно В (А = В), если для
- 5. Операции над множествами Определение. Пересечением множеств А и В называется множество, состоящее из всех тех и
- 6. Объединением множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат хотя бы
- 7. Определение Пусть А и В множества. Разностью множеств А – В называется множество всех тех и
- 8. Теорема Для произвольных множеств А и В справедливо равенство А – В = А ∩ В'
- 9. Теорема Для произвольных множеств А и В имеет место а) (А ∩ В)' = А' ∪
- 10. Теорема Для произвольных множеств А, В и С справедливы равенства а) А ∩ (В ∪ С)
- 11. Определение Множество всех подмножеств множества А, или булеан множества А, обозначается P (A), есть множество, состоящее
- 12. Пусть А = {1, 2, 3}, и В = {r, s}. Тогда A × B =
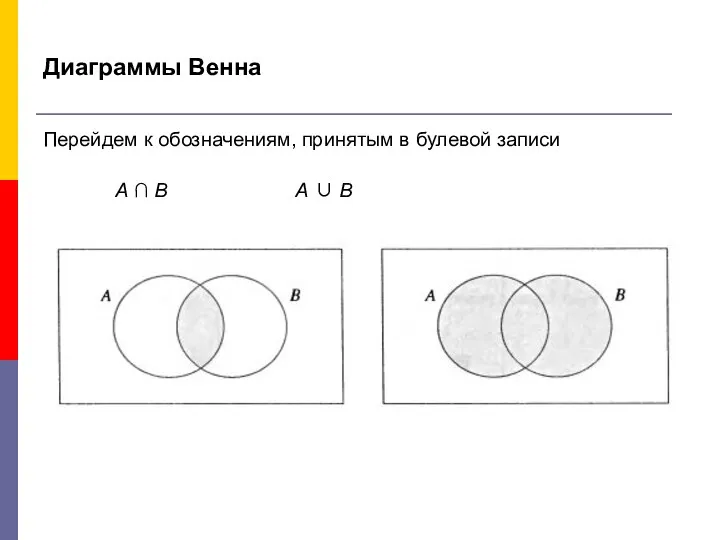
- 13. Диаграммы Венна Перейдем к обозначениям, принятым в булевой записи А ∩ В А ∪ В
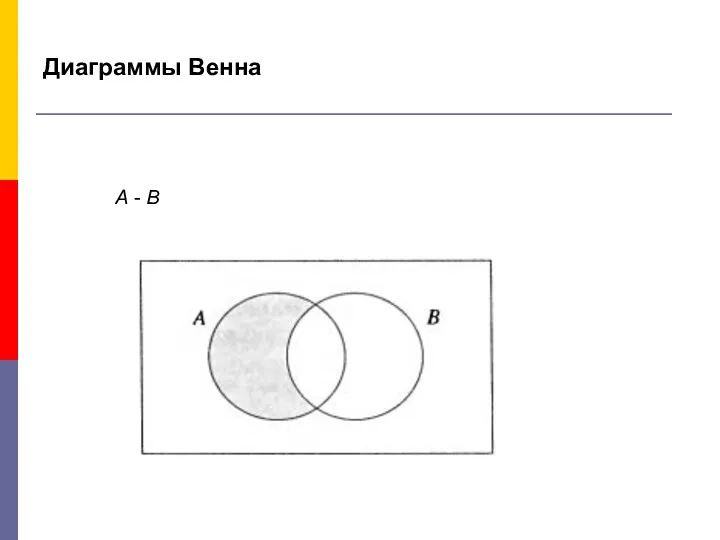
- 14. Диаграммы Венна А - В
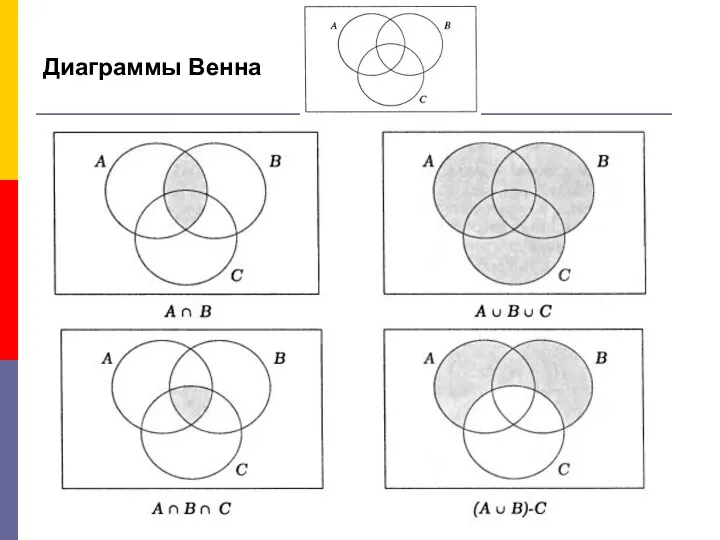
- 15. Диаграммы Венна
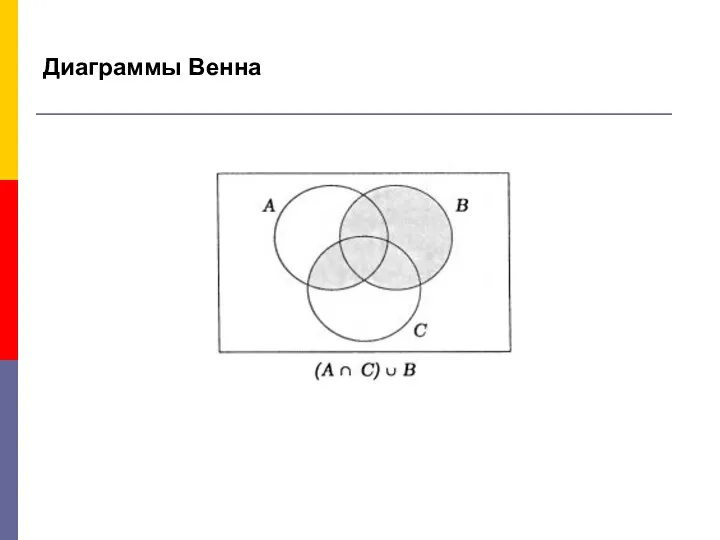
- 16. Диаграммы Венна
- 17. Теорема Пусть А, В и С – подмножества универсального множества U . Тогда справедливы
- 20. Мощность
- 21. Определение Мощность множества есть просто количество содержащихся в нем элементов. Пустое множество есть конечное множество мощности
- 22. Теорема а) Пусть А и В – непересекающиеся конечные множества. Тогда множество А ∪ В конечно.
- 23. Теорема. Пусть S – счетно бесконечное множество, тогда множество S×S также счетно бесконечное. Доказательство: Если N
- 24. По диагональным стрелкам определяют соотношение φ: φ(1)=(1, 1), φ(2)=(1, 2), φ(3)=(2, 1), φ(4)=(1, 3), φ(5)=(2, 3)…
- 25. Теорема. Множество Q+ положительных рациональных чисел является счетно бесконечным. Доказательство: Рассмотрим подмножество М множества N ×
- 26. Теорема. Если А и В – счетные множества, то А ∪ В также счетно. Доказательство: Множество
- 27. Теорема. Пусть R – множество действительных чисел. Множество I = {x : x ∈ R и
- 28. Теорема. Множество действительных R несчетно. Доказательство: Если бы R было счетным, то множество I ⊆ R
- 29. Теорема. Не существует взаимно однозначного соответствия между множеством S и его булеаном P(S).
- 30. Пример (Парадокс Рассела) Пусть S – множество всех множеств. Пусть W = {x : x ∉x
- 32. Скачать презентацию

























 математика Петерсон 2 класс Таблица умножения и деления с презентацией
математика Петерсон 2 класс Таблица умножения и деления с презентацией Прикладная статистика. Меры центральной тенденции. Меры разброса. Нормальное распределение
Прикладная статистика. Меры центральной тенденции. Меры разброса. Нормальное распределение Случайная величина (СВ) и закон ее распределения
Случайная величина (СВ) и закон ее распределения Геометрические преобразования пространства
Геометрические преобразования пространства ИКТ при изучении темы Разные задачи на многогранники, цилиндр, конус и шар
ИКТ при изучении темы Разные задачи на многогранники, цилиндр, конус и шар Взаємне розміщення площини і кулі у просторі
Взаємне розміщення площини і кулі у просторі Презентация Счёт в пределах 1000
Презентация Счёт в пределах 1000 Формы организации учебной деятельности учащихся на уроке математики
Формы организации учебной деятельности учащихся на уроке математики Обыкновенные дроби. Деление дробей
Обыкновенные дроби. Деление дробей Методическое пособие по математике Состав числа 6
Методическое пособие по математике Состав числа 6 Математический турнир знатоков, 8 класс
Математический турнир знатоков, 8 класс Повторение теоретического материала по геометрии 7 класс
Повторение теоретического материала по геометрии 7 класс Математический анализ
Математический анализ Параллелепипед. Грани, ребра, диагональ параллелепипеда
Параллелепипед. Грани, ребра, диагональ параллелепипеда Сумма углов треугольника. Тренировочные упражнения
Сумма углов треугольника. Тренировочные упражнения Матрицы. Метод Гаусса. Формулы Крамера
Матрицы. Метод Гаусса. Формулы Крамера Некоторые следствия из аксиом
Некоторые следствия из аксиом Числа-иероглифы в Древнем Египте
Числа-иероглифы в Древнем Египте Скалярное произведение векторов. Вычисление углов между прямыми
Скалярное произведение векторов. Вычисление углов между прямыми Неравенство треугольника
Неравенство треугольника Тренажёр по математике (2 класс)
Тренажёр по математике (2 класс) Метод координат
Метод координат Формула корней квадратного уравнения
Формула корней квадратного уравнения Прямая и обратная пропорциональные зависимости
Прямая и обратная пропорциональные зависимости Арифметический квадратный корень
Арифметический квадратный корень История комплексных чисел от Кардано до Гамильтона
История комплексных чисел от Кардано до Гамильтона Внеурочное мероприятие по математике В гостях у Квадратика в специальном классе школы 8 вида
Внеурочное мероприятие по математике В гостях у Квадратика в специальном классе школы 8 вида Деление с остатком
Деление с остатком