Задание 2. Упростите логическое выражение
F= (A v B)→ (B v
C).
Избавимся от импликации и отрицания. Воспользуемся (¬(A→B)=A& ¬ B). Получится: ¬((AvB)→ ¬(BvC))= (AvB)& ¬ (¬(BvC)).
Применим закон двойного отрицания, получим:
(A v В) & ¬(¬(В v С)) = (A v В) & (B v С).
Применим правило дистрибутивности ((A∙B) +(A∙C) = A∙(B+C)). Получим: (AvВ)& (B v С)= (AvB)&Bv(AvB)&C
Применим закон коммутативности (A&B=B&A ) и дистрибутивности (16). Получим: (AvB)&Bv(AvB)&C = A&BvB&BvA&CvB&C.
Применим (А& A= A) и получим: A&BvB&BvA&CvB&C= A&BvBvA&CvB&C
Применим ((A&B) v(A&C) = A&(BvC) ), т.е. вынесем за скобки В.
Получим:A&BvBvA&CvB&C= B& (Av1)vA&CvB&C.
Применим (Аv 1= 1 ). Получим:B& (Av1) vA&CvB&C= BvA&CvB&C.
Переставим местами слагаемые, сгруппируем и вынесем В за скобки. Получим:BvA&CvB&C = B& (1vC)vA&C.
Применим (Аv 1= 1 ) и получим ответ: B&(1vC)vA&C=BvA&C.












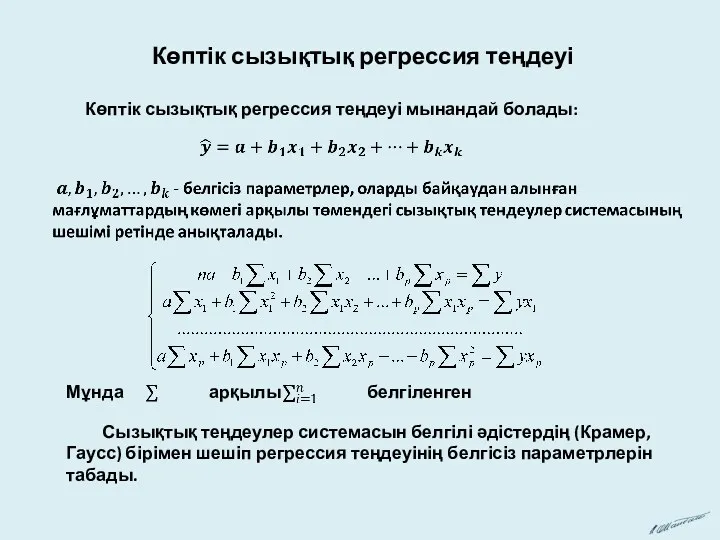 Көптік сызықтық регрессия теңдеуі
Көптік сызықтық регрессия теңдеуі Умножение.
Умножение. Некоторые сведения из теории множеств
Некоторые сведения из теории множеств Усеченная пирамида
Усеченная пирамида Графическое решение квадратных уравнений
Графическое решение квадратных уравнений Касательная к окружности. Свойство отрезков касательных
Касательная к окружности. Свойство отрезков касательных Конспект и презентация к уроку-путешествию в лес, математика 1 класс Закрепление навыков сложения и вычитания в пределах 20
Конспект и презентация к уроку-путешествию в лес, математика 1 класс Закрепление навыков сложения и вычитания в пределах 20 Математикалық ойын
Математикалық ойын Конспект урока по математике 2 класс УМК Петерсон Л.Г. Свойства сложения + презентация
Конспект урока по математике 2 класс УМК Петерсон Л.Г. Свойства сложения + презентация Симметрия - математический закон красоты
Симметрия - математический закон красоты Trigonometric Identities. Lesson 7.1
Trigonometric Identities. Lesson 7.1 Свойства степени с натуральным показателем
Свойства степени с натуральным показателем Линейная алгебра. Ранг матрицы. (Тема 2)
Линейная алгебра. Ранг матрицы. (Тема 2) Признаки делимости на 9 и на 3
Признаки делимости на 9 и на 3 Множественная линейная регрессия
Множественная линейная регрессия Математика. 1 класс. Урок 3. Размер
Математика. 1 класс. Урок 3. Размер Рациональные уравнения, как математические модели реальных ситуаций
Рациональные уравнения, как математические модели реальных ситуаций Геометрические фигуры. Занятие для дошкольников
Геометрические фигуры. Занятие для дошкольников Понятие переменной.
Понятие переменной. Сумма и разность синусов. Сумма и разность косинусов. 10 класс (алгебра)
Сумма и разность синусов. Сумма и разность косинусов. 10 класс (алгебра) Պյութագորասի թեորեմը և հակադարձ թեորեմը
Պյութագորասի թեորեմը և հակադարձ թեորեմը Прямая и отрезок. Провешивание прямой на местности
Прямая и отрезок. Провешивание прямой на местности Игра-тренажер по математике.
Игра-тренажер по математике. Пересечение поверхностей, одна из которых проецирующая. Пересечение полусферы и проецирующего цилиндра
Пересечение поверхностей, одна из которых проецирующая. Пересечение полусферы и проецирующего цилиндра Дискретная математика. Часть 2 Отношения на множествах и элементы комбинаторики
Дискретная математика. Часть 2 Отношения на множествах и элементы комбинаторики Решение систем рациональных неравенств. 9 класс
Решение систем рациональных неравенств. 9 класс Производная. Устные упражнения
Производная. Устные упражнения Деление с остатком
Деление с остатком