Содержание
- 2. Численные методы Тема 1. Решение уравнений © К.Ю. Поляков, 2008
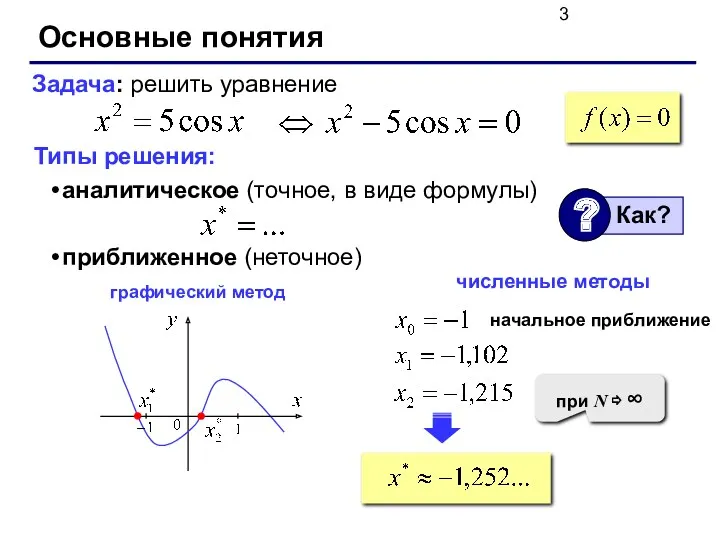
- 3. Основные понятия Типы решения: аналитическое (точное, в виде формулы) приближенное (неточное) Задача: решить уравнение численные методы
- 4. Численные методы Идея: последовательное уточнение решения с помощью некоторого алгоритма. Область применения: когда найти точное решение
- 5. Есть ли решение на [a, b]? есть решение нет решения нет решения
- 6. Метод дихотомии (деление пополам) Найти середину отрезка [a,b]: c = (a + b) / 2; Если
- 7. Метод дихотомии (деления пополам) простота можно получить решение с заданной точностью (в пределах точности машинных вычислений)
- 8. Метод деления отрезка пополам //---------------------------------------------- // BinSolve находит решение на [a,b] // методом деления отрезка пополам
- 9. Как подсчитать число шагов? float BinSolve ( float a, float b, float eps, int &n )
- 10. Метод итераций (повторений) Задача: Эквивалентные преобразования: имеет те же решения при Идея решения: – начальное приближение
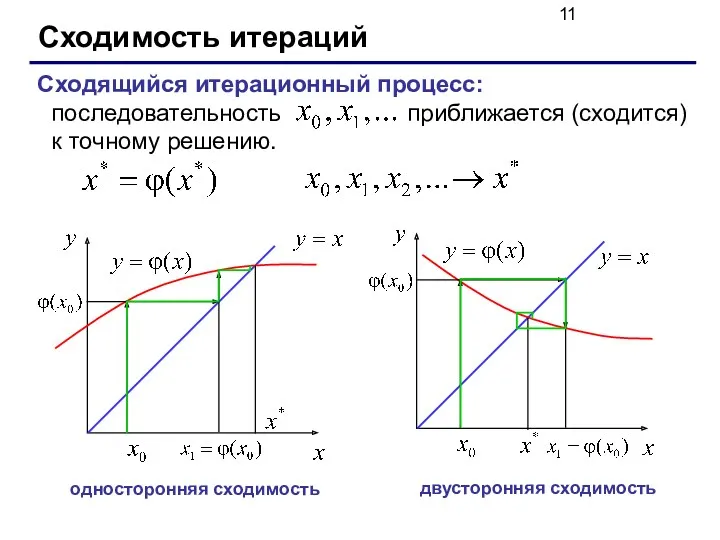
- 11. Сходимость итераций Сходящийся итерационный процесс: последовательность приближается (сходится) к точному решению. односторонняя сходимость двусторонняя сходимость
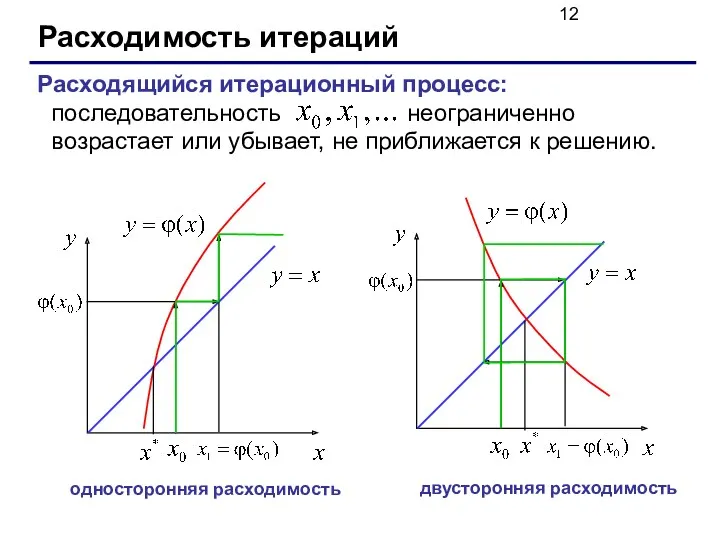
- 12. Расходимость итераций Расходящийся итерационный процесс: последовательность неограниченно возрастает или убывает, не приближается к решению. односторонняя расходимость
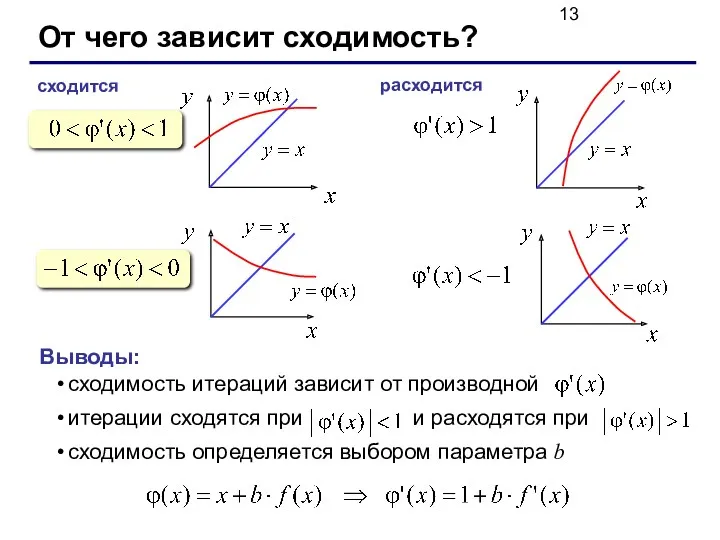
- 13. От чего зависит сходимость? сходится расходится Выводы: сходимость итераций зависит от производной итерации сходятся при и
- 14. Как выбрать b? наугад, пробовать разные варианты для начального приближения x0 пересчитывать на каждом шаге, например:
- 15. Метод итераций (программа) //---------------------------------------------- // Iter решение уравнения методом итераций // Вход: x – начальное приближение
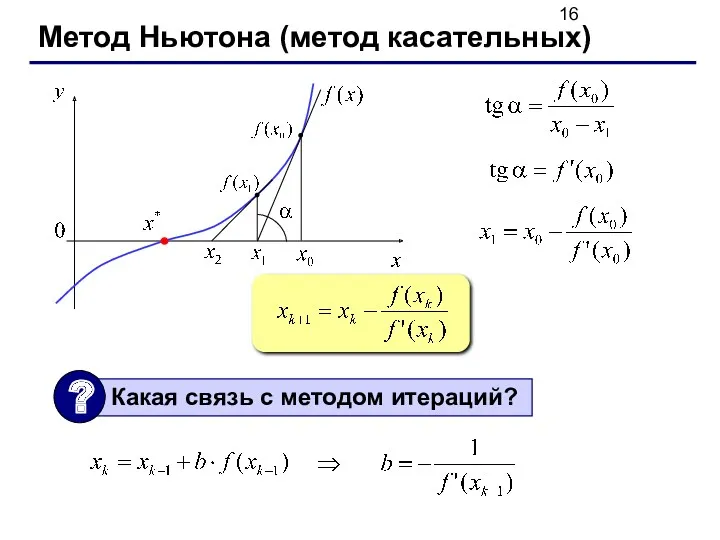
- 16. Метод Ньютона (метод касательных)
- 17. Метод Ньютона (программа) //---------------------------------------------- // Newton решение уравнения методом Ньютона // Вход: x – начальное приближение
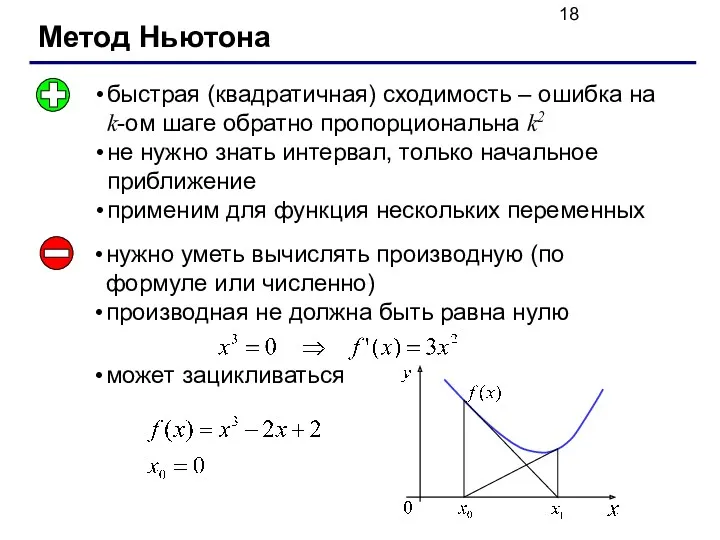
- 18. Метод Ньютона быстрая (квадратичная) сходимость – ошибка на k-ом шаге обратно пропорциональна k2 не нужно знать
- 19. Численные методы Тема 2. Вычисление площади (интеграла) © К.Ю. Поляков, 2008
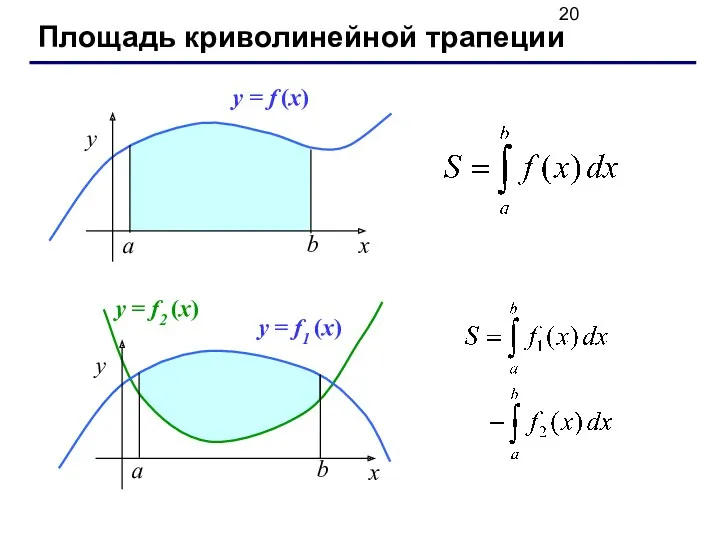
- 20. Площадь криволинейной трапеции
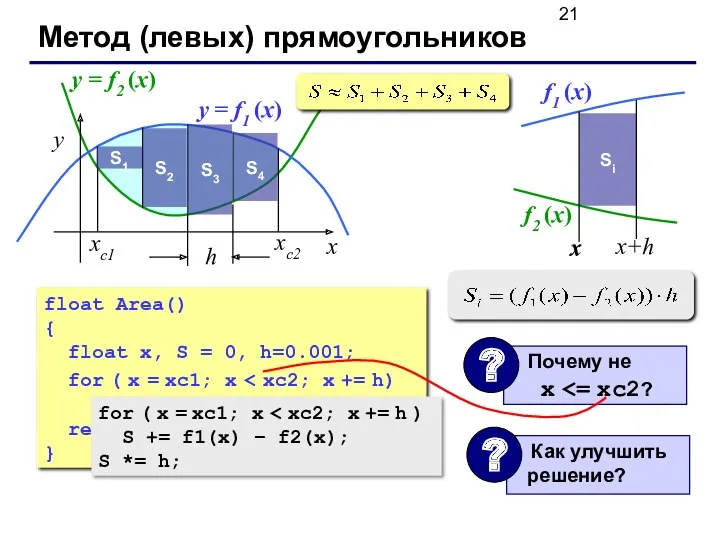
- 21. Метод (левых) прямоугольников y = f1 (x) y = f2 (x) S1 S2 S3 S4 float
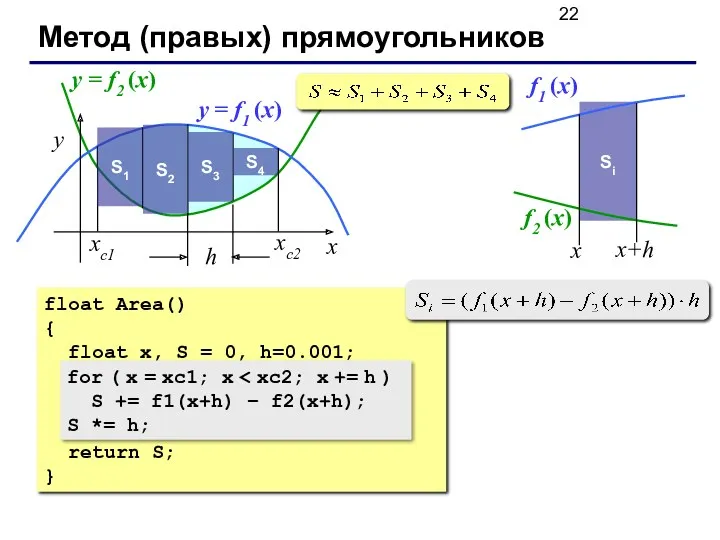
- 22. Метод (правых) прямоугольников x y xс2 xс1 y = f1 (x) y = f2 (x) S1
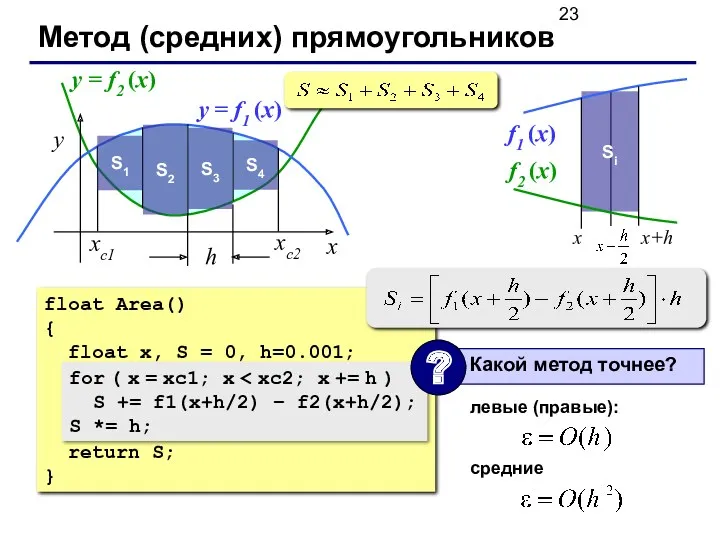
- 23. Метод (средних) прямоугольников x y xс2 xс1 y = f1 (x) y = f2 (x) S1
- 24. Метод трапеций x y xс2 xс1 y = f1 (x) y = f2 (x) for (
- 25. Метод Монте-Карло Применение: вычисление площадей сложных фигур (трудно применить другие методы). Требования: необходимо уметь достаточно просто
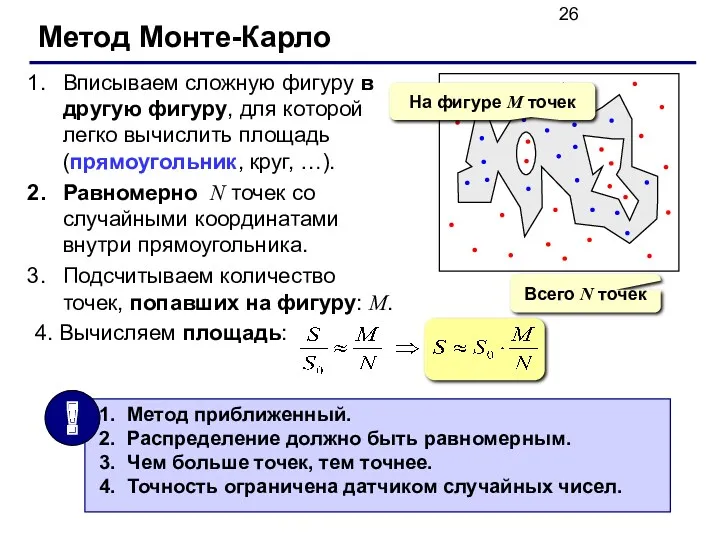
- 26. Метод Монте-Карло Вписываем сложную фигуру в другую фигуру, для которой легко вычислить площадь (прямоугольник, круг, …).
- 27. Численные методы Тема 3. Вычисление длины кривой © К.Ю. Поляков, 2008
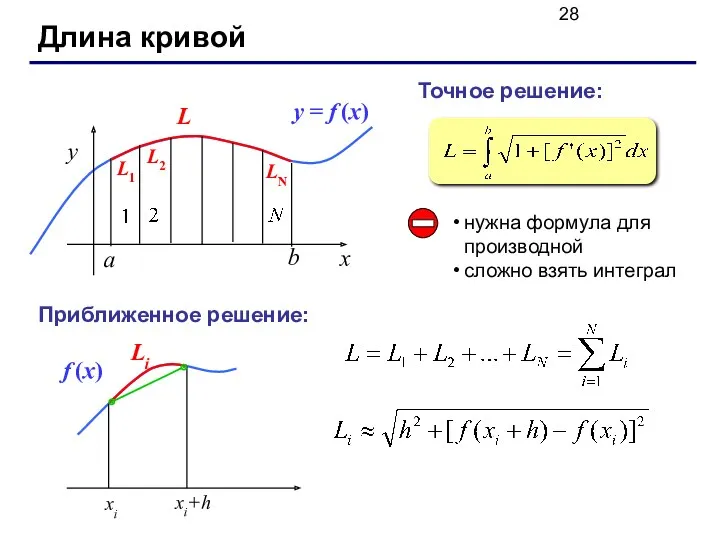
- 28. Длина кривой Точное решение: нужна формула для производной сложно взять интеграл Приближенное решение:
- 29. Длина кривой //---------------------------------------------- // CurveLen вычисление длины кривой // Вход: a, b – границы интервала //
- 30. Численные методы Тема 4. Оптимизация © К.Ю. Поляков, 2008
- 31. Найти x, при котором или при заданных ограничениях. Основные понятия Оптимизация – поиск оптимального (наилучшего в
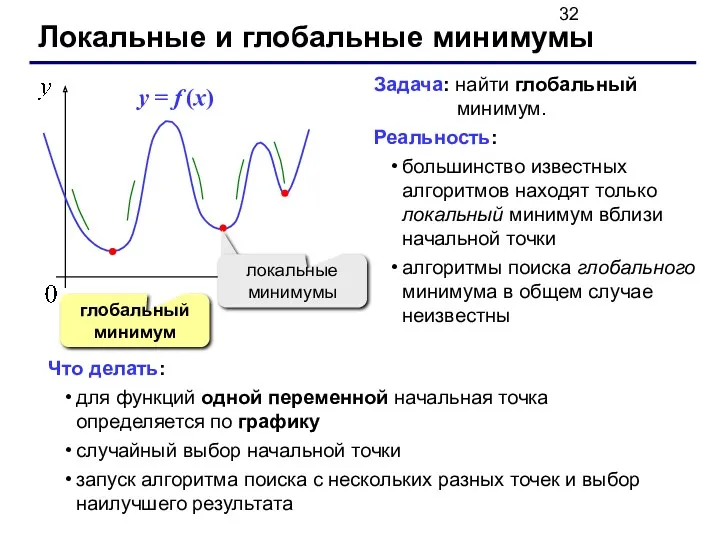
- 32. Локальные и глобальные минимумы глобальный минимум Задача: найти глобальный минимум. Реальность: большинство известных алгоритмов находят только
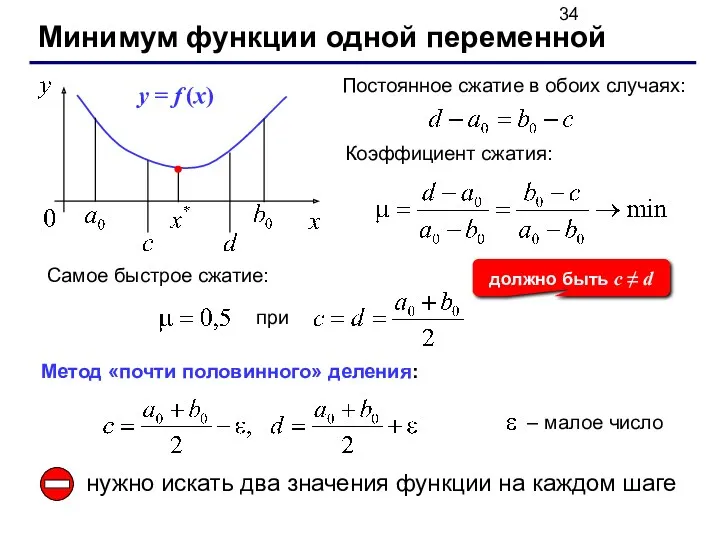
- 33. Минимум функции одной переменной Дано: на интервале [a,b] функция непрерывна и имеет единственный минимум. Найти: x*
- 34. Минимум функции одной переменной Коэффициент сжатия: Самое быстрое сжатие: при должно быть c ≠ d Метод
- 35. Отношение «золотого сечения» Идея: выбрать c и d так, чтобы на каждом шаге вычислять только одно
- 36. Метод «золотого сечения» //---------------------------------------------- // Gold поиск минимума функции («золотое сечение») // Вход: a, b –
- 37. Функции нескольких переменных Проблемы: нет универсальных алгоритмов поиска глобального минимума неясно, как выбрать начальное приближение (зависит
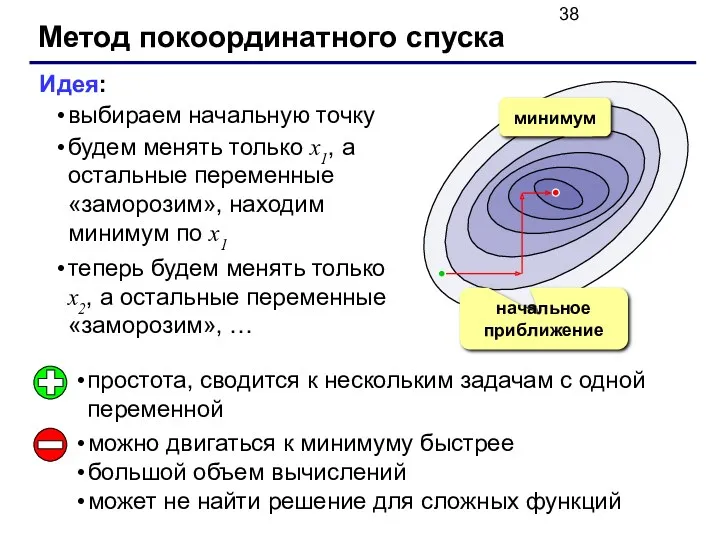
- 38. Метод покоординатного спуска Идея: выбираем начальную точку будем менять только x1, а остальные переменные «заморозим», находим
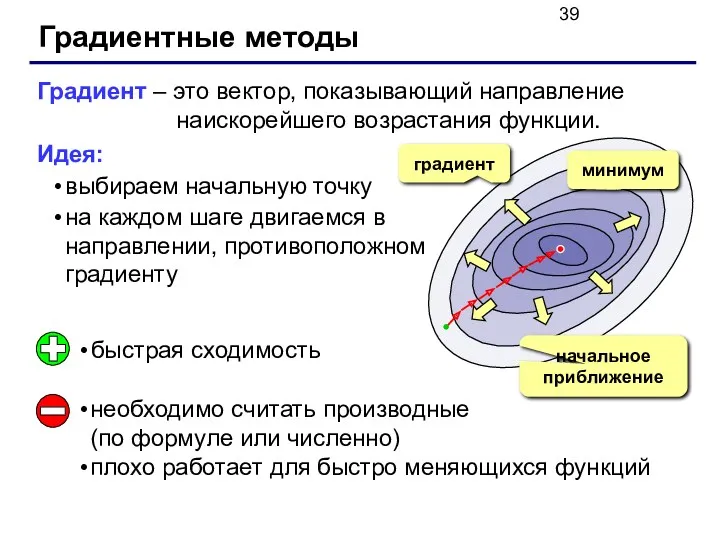
- 39. Градиентные методы Градиент – это вектор, показывающий направление наискорейшего возрастания функции. Идея: выбираем начальную точку на
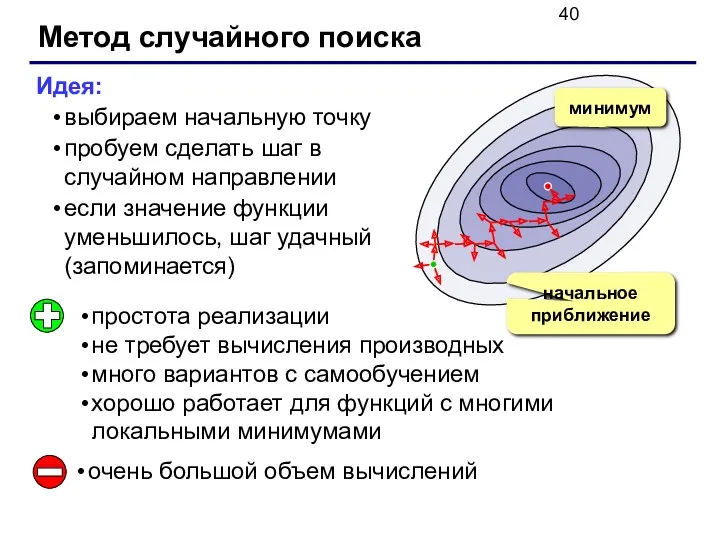
- 40. Метод случайного поиска Идея: выбираем начальную точку пробуем сделать шаг в случайном направлении если значение функции
- 42. Скачать презентацию


![Есть ли решение на [a, b]? есть решение нет решения нет решения](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/375445/slide-4.jpg)
![Метод дихотомии (деление пополам) Найти середину отрезка [a,b]: c =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/375445/slide-5.jpg)














![Минимум функции одной переменной Дано: на интервале [a,b] функция непрерывна](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/375445/slide-32.jpg)



 Арифметическая прогрессия. Применение формул
Арифметическая прогрессия. Применение формул Квадратичная функция и ее график. Урок алгебры. 9 класс
Квадратичная функция и ее график. Урок алгебры. 9 класс Задачі на дві дії різного ступеня: множення і додавання або віднімання (2 клас)
Задачі на дві дії різного ступеня: множення і додавання або віднімання (2 клас) Математический калейдоскоп
Математический калейдоскоп Сравнение с помощью координатного луча
Сравнение с помощью координатного луча Засоби розв'язання задач оптимізації
Засоби розв'язання задач оптимізації Первые представления о решение рациональных уравнений. 8 класс
Первые представления о решение рациональных уравнений. 8 класс Эконометрика. Нелинейные модели. Логит- и пробит-модели. Лекции
Эконометрика. Нелинейные модели. Логит- и пробит-модели. Лекции Площадь многоугольника
Площадь многоугольника Введение декартовых координат в пространстве. Расстояние между точками. Координаты середины отрезка
Введение декартовых координат в пространстве. Расстояние между точками. Координаты середины отрезка Круговые диаграммы
Круговые диаграммы Урок+презентация по математике Арифметический корень натуральной степени и его свойства для 9 класса
Урок+презентация по математике Арифметический корень натуральной степени и его свойства для 9 класса Презентация по математике по теме урока: Знакомимся с задачей, 1 класс
Презентация по математике по теме урока: Знакомимся с задачей, 1 класс Презентация Устный счёт 2 класс 1 четверть № 4
Презентация Устный счёт 2 класс 1 четверть № 4 Пифагор Самосский - великий древнегреческий математик
Пифагор Самосский - великий древнегреческий математик Сложение и умножение дробей с одинаковыми знаменателями. Технологическая карта урока по математике в 5 классе
Сложение и умножение дробей с одинаковыми знаменателями. Технологическая карта урока по математике в 5 классе Презентация к уроку математики во 2 классе по теме Применение сложения и вычитания в разных ситуациях
Презентация к уроку математики во 2 классе по теме Применение сложения и вычитания в разных ситуациях Свойства действий с рациональными числами. Часть 2
Свойства действий с рациональными числами. Часть 2 Елементи комбінаторики. Комбінаторні задачі
Елементи комбінаторики. Комбінаторні задачі Графический способ решения систем уравнений. 9 класс
Графический способ решения систем уравнений. 9 класс Обучение младших школьников решению нестандартных олимпиадных задач
Обучение младших школьников решению нестандартных олимпиадных задач Степень с целым показателем. 8 класс
Степень с целым показателем. 8 класс Искусственные нейронные сети
Искусственные нейронные сети Omówienie sprawdzianu
Omówienie sprawdzianu Измерение углов. Транспортир
Измерение углов. Транспортир Часть II. Случайные величины
Часть II. Случайные величины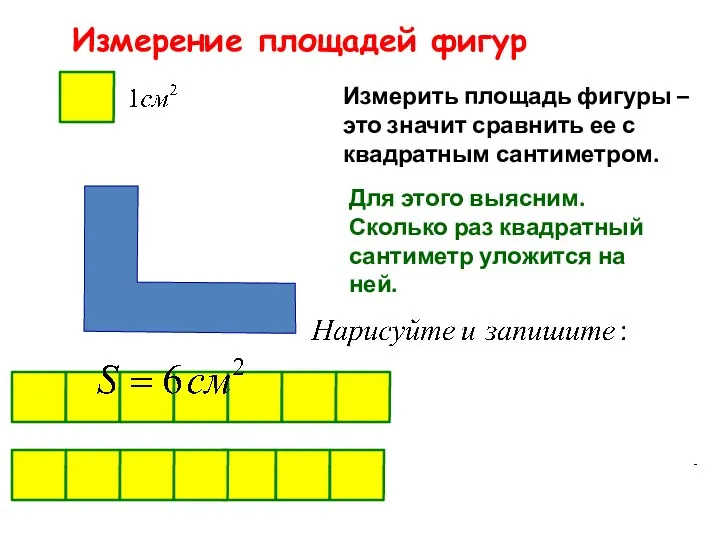 Измерение площадей фигур
Измерение площадей фигур Логарифмы
Логарифмы