Содержание
- 2. 1.1. Понятие числового ряда Пусть – числовая последовательность. Выражение вида называется числовым рядом, числа – члены
- 3. Ряд (1) считается заданным, если известен общий член ряда, выраженный как функция его номера n: Сумма
- 4. Если для последовательности частичных сумм ряда (1) существует конечный предел то ряд (1) называется сходящимся, а
- 5. Пример Ряд 0+0+0+...+0+... сходится, его сумма S=0. Ряд 1+1+1+...+1+... расходится, так как предел Ряд 1-1+1-1+... расходится,
- 6. Свойства рядов 1. Если к ряду (1) прибавить или отбросить конечное число его членов, то полученный
- 7. 3. Если ряды и сходятся и их суммы соответственно равны и то сходится ряд и его
- 8. Замечания 1. Из свойства 3 вытекает, что сумма (разность) сходящегося и расходящегося рядов есть расходящийся ряд.
- 9. Ряд называется n-м остатком ряда (1). Он получается из ряда (1) отбрасыванием n первых его членов.
- 10. Из свойства 1 также следует , что если ряд (1) сходится, то его остаток стремится к
- 11. Необходимый признак сходимости ряда Если ряд сходится, то общий член ряда стремится к нулю при ,
- 12. Достаточный признак расходимости ряда Если или не существует, то ряд расходится.
- 13. Пример Исследовать сходимость ряда Решение. 1. Найдем предел общего члена ряда:
- 14. 2.
- 15. §2. Достаточные признаки сходимости рядов с положительными членами
- 16. Первый признак сравнения Если для членов рядов справедливо неравенство для всех , то из сходимости ряда
- 17. Второй признак сравнения Пусть и – ряды с положительными членами, причем существует конечный и отличный от
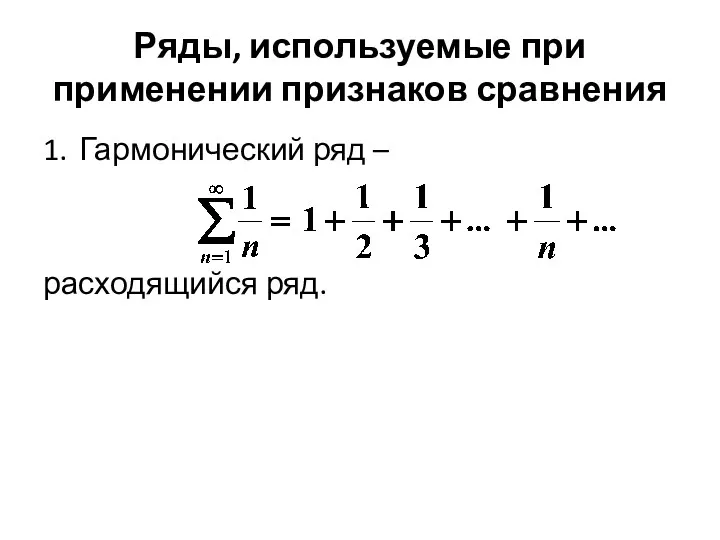
- 18. Ряды, используемые при применении признаков сравнения 1. Гармонический ряд – расходящийся ряд.
- 19. 2. Ряд, составленный из членов геометричес-кой прогрессии, при сходится и его сумма равна при расходится.
- 20. Обобщенный гармонический ряд при сходится, при расходится.
- 21. Пример Ряд – сходится (как обобщенный гармонический при 2. Ряд – расходится (как обобщенный гармонический при
- 22. Признак Даламбера Пусть – ряд с положительными членами, и существует конечный предел Тогда, если , то
- 23. Если то ряд может сходиться или расходиться. Ряд требуется исследовать с помощью других признаков сходимости.
- 24. Вспомогательные сведения
- 25. Пример Записать общий член ряда, 2 первых члена ряда и (n+1 )-й член ряда. Решение. Формула
- 26. Подставляя в формулу общего члена ряда вместо n значения 1, 2, n+1, получим
- 27. 2. Используя признак Даламбера исследовать ряд на сходимость. Решение. общий член ряда: (n+1)-й член ряда:
- 28. Найдем По признаку Даламбера ряд сходится.
- 29. §3. ЗНАКОЧЕРЕДУЮЩИЕСЯ РЯДЫ
- 30. 3.1. Знакочередующиеся ряды Ряд вида где для всех называется знакочередующимся.
- 31. Признак Лейбница Пусть дан знакочередующийся ряд (4). Если выполнены два условия последовательность абсолютных величин членов ряда
- 32. Замечания 1. Ряды вида (4), для которых выполняются условия теоремы Лейбница, называются лейбницевскими (или рядами Лейбница).
- 33. Отброшенный ряд (остаток) представляет собой также знакочередующийся ряд сумма которого по модулю меньше первого члена этого
- 34. Абсолютная сходимость Знакочередующийся ряд называется абсолютно сходящимся, если ряд, составленный из модулей его членов, сходится. В
- 35. Пример Исследовать на сходимость ряд Решение. Исследуем на сходимость ряд из модулей: Это обобщенный гармонический ряд
- 36. Выясним, сходится ли он условно. Используем признак Лейбница: последовательность абсолютных величин членов ряда монотонно убывает: общий
- 38. Скачать презентацию












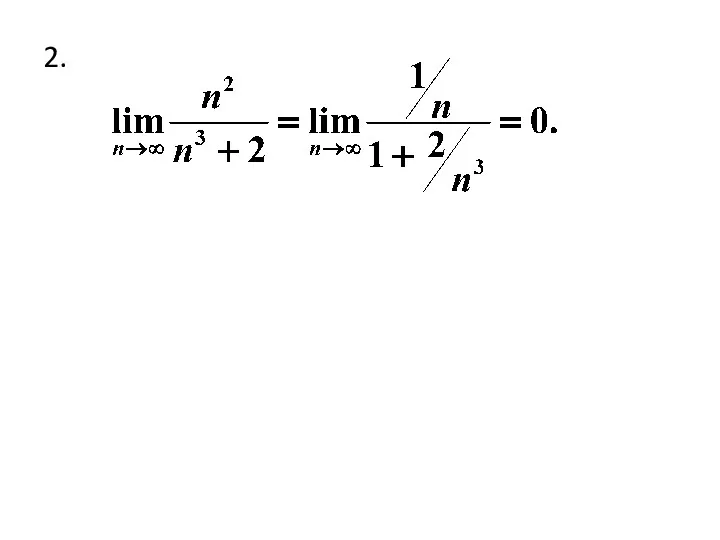





















 Фракталы в музыке
Фракталы в музыке время,скорость, расстояние
время,скорость, расстояние Разработка и проведение дидактических игр на материале заданий ОГЭ по математике
Разработка и проведение дидактических игр на материале заданий ОГЭ по математике Марковские системы массового обслуживания
Марковские системы массового обслуживания Векторная алгебра. Векторы на плоскости и в пространстве
Векторная алгебра. Векторы на плоскости и в пространстве Корень n-й степени
Корень n-й степени Параллельные плоскости и их свойства
Параллельные плоскости и их свойства Повторення вивченого. Додаткові вправи. Урок №136
Повторення вивченого. Додаткові вправи. Урок №136 Системы уравнений второй степени
Системы уравнений второй степени Квадрат түбірі бар өрнектерді түрлендіру
Квадрат түбірі бар өрнектерді түрлендіру Урок-путешествие: Галактика- математика.
Урок-путешествие: Галактика- математика. Производная в технике, физике и химии
Производная в технике, физике и химии Прямоугольные треугольники и некоторые их свойства
Прямоугольные треугольники и некоторые их свойства Величина угла. Измерение углов
Величина угла. Измерение углов Обработка результатов измерений
Обработка результатов измерений Фаррахов Динар, 7 в, (необычные способы вычислений )
Фаррахов Динар, 7 в, (необычные способы вычислений ) Царстве математики. 6 класс
Царстве математики. 6 класс Узагальнення і систематизація вивченого. Урок №131. Математика
Узагальнення і систематизація вивченого. Урок №131. Математика Разработка урока математики во 2 классе с использованием ИКТ
Разработка урока математики во 2 классе с использованием ИКТ Решение уравнений. Раскройте скобки
Решение уравнений. Раскройте скобки Сложение и умножение вероятностей
Сложение и умножение вероятностей Урок математики в 1 класс по теме Сложение с нулем дидактическая система Л.В.Занкова
Урок математики в 1 класс по теме Сложение с нулем дидактическая система Л.В.Занкова Мультимедийный урок математики по теме Периметр многоугольника
Мультимедийный урок математики по теме Периметр многоугольника Математическая статистика
Математическая статистика Блеф клуб. Математическая игра для учащихся 7-х классов
Блеф клуб. Математическая игра для учащихся 7-х классов Программа элективного курса. Тема: “Мир, математика, математики”
Программа элективного курса. Тема: “Мир, математика, математики” Решение задач на составление уравнений
Решение задач на составление уравнений Приемы сравнения чисел
Приемы сравнения чисел