Слайд 2

§ 1. Понятие функции двух переменных.
Слайд 3

Пусть x, y – две независимые друг от друга переменные. Графически
пару независимых переменных (x, y) можно представить как точку M(x, y) на плоскости xOy. Пусть D – некоторое множество точек M(x, y).
Слайд 4

Опр. Если каждой точке M(x, y) из множества D по некоторому закону
f ставится в соответ-ствие вполне определенное действительное число z, то говорят, что z есть функция двух переменных x и y и пишут
z = f(x, y) или z = f(M),
где M = M(x, y) – точка плоскости.
Слайд 5

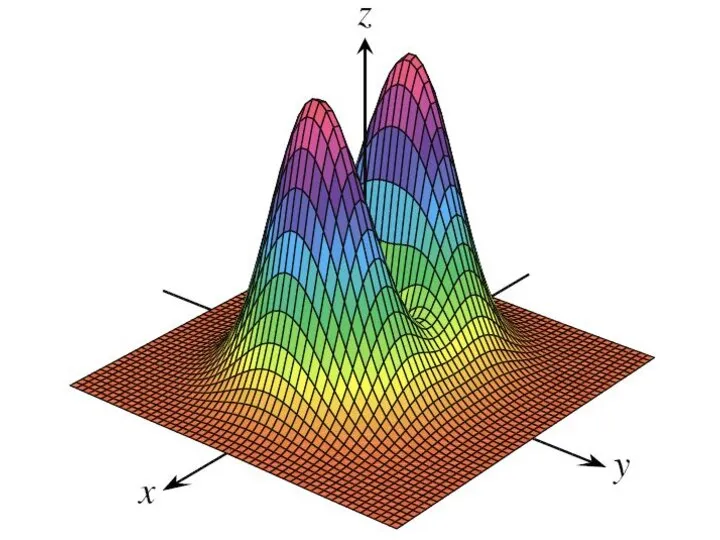
Геометрическим изображением функции двух переменных является некоторая поверхность в трехмерном пространстве.
Слайд 6
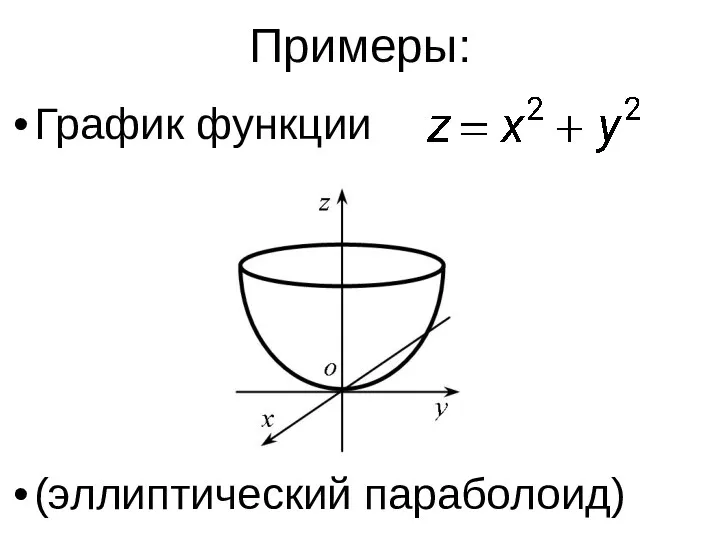
Примеры:
График функции
(эллиптический параболоид)
Слайд 7
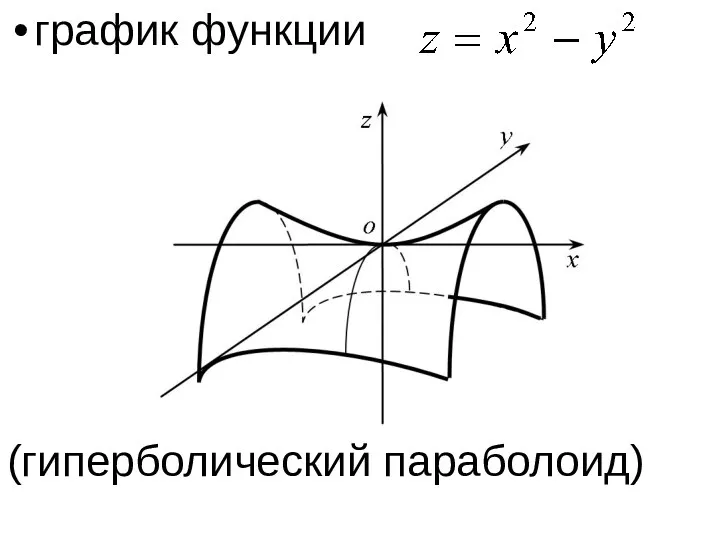
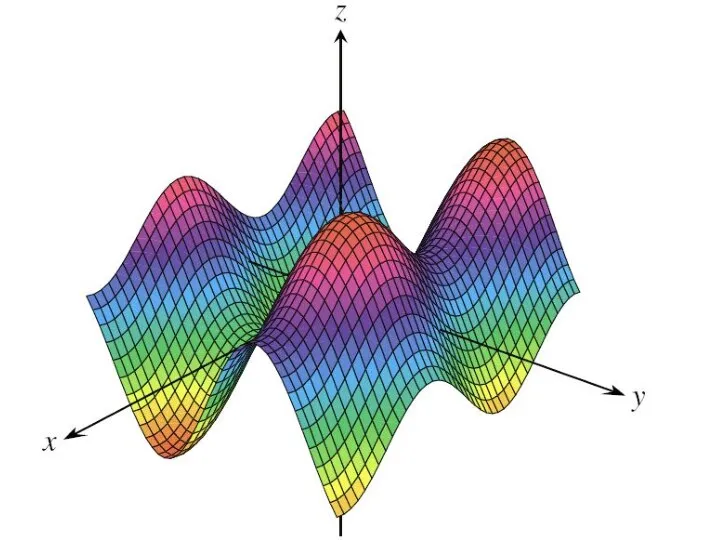
график функции
(гиперболический параболоид)
Слайд 8
Слайд 9
Слайд 10

Опр. Областью определения функции z = f(x, y) называется множество D точек M(x, y), в
которых функция z = f(x, y) определена и может быть вычислена. Все значения, которые принимает функция z = f(x, y) (в области ее определения), образуют множество значений функции.
Слайд 11

Слайд 12

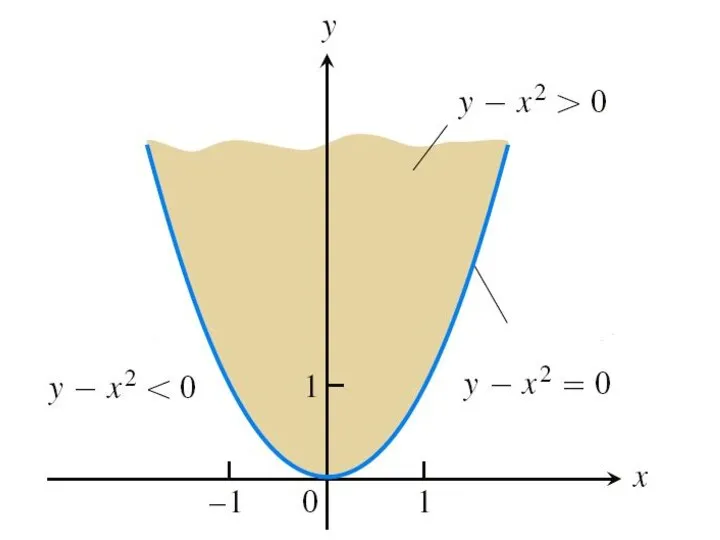
Графическое изображение области определения функции.
Пример. Построим область определения функции
Слайд 13
Слайд 14

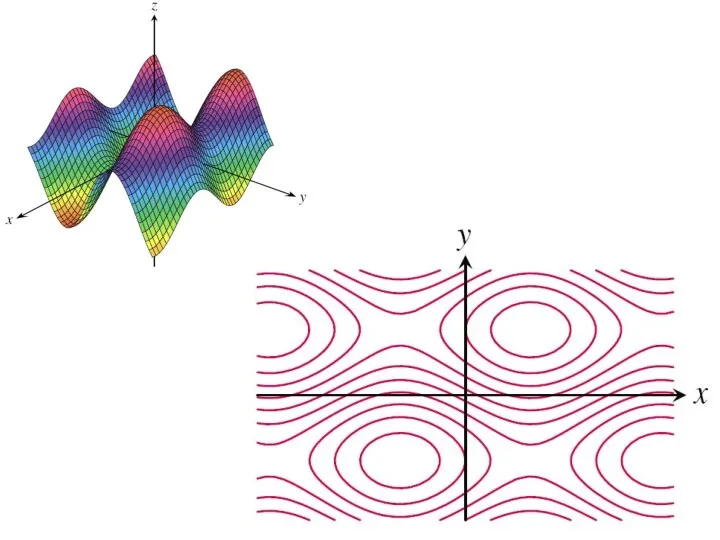
Линии уровня
Опр. Множество точек плоскости таких, что функция f(x, y) принимает в
них одно и то же значение, f(x, y) = c, называется линией уровня.
Слайд 15
Слайд 16
Слайд 17
Слайд 18
Слайд 19

Построение графика функции двух переменных
Рассмотрим пример построения графика функции
Слайд 20

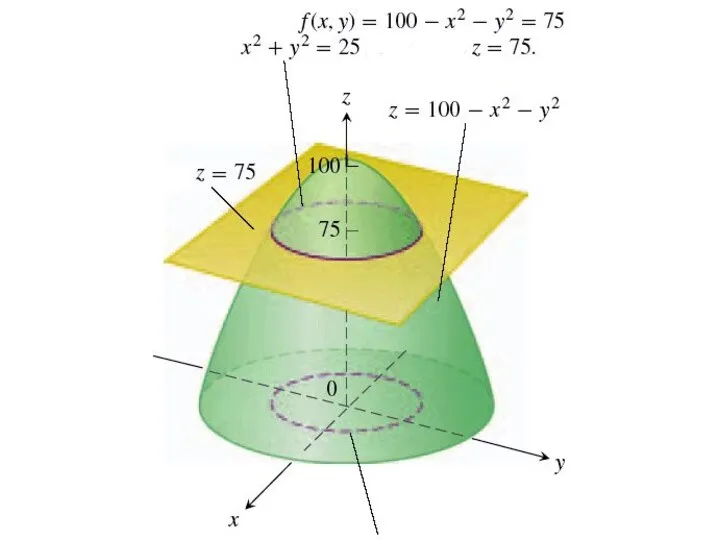
Зафиксируем какое-нибудь значение этой функции, например, z = 75. Тем самым мы определили
в пространстве плоскость z = 75. Находим линию уровня при z = 75:
100 – x2 – y2 = 75, откуда x2 + y2 = 25 – уравнение окружности.
Слайд 21
Слайд 22

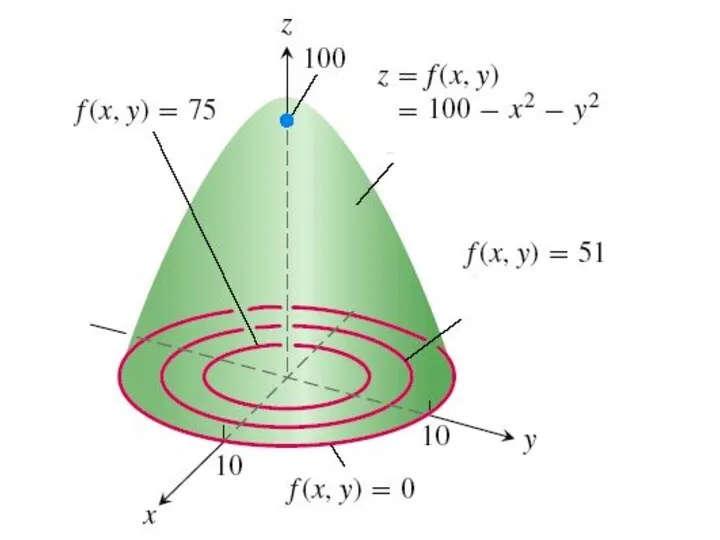
Находя множество линий уровня, строим весь график.
Слайд 23
Слайд 24

§ 2. Понятие функции трех и более переменных.
Всякая упорядоченная совокупность действительных
чисел (x1, x2, …, xn) называется точкой n–мерного пространства Rn. Пусть D – некоторое мно-жество точек пространства Rn.
Слайд 25

Опр. Если каждой точке M(x1, x2, …, xn) из области D по некоторому закону
f ставится в сответствие вполне определенное число u, то говорят, что u есть функция n переменных и пишут
u = f(x1, x2, …, xn) или u = f(M)
где M = M(x1, x2, …, xn) – точка n–мерного пространства.
Слайд 26

Слайд 27

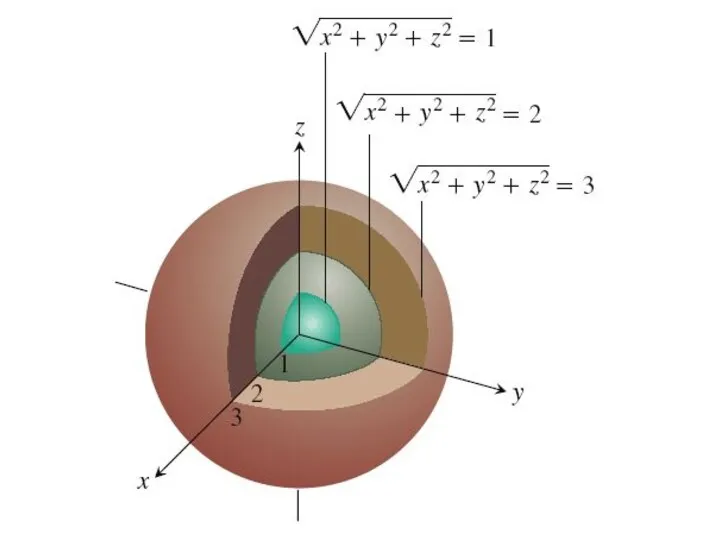
Опр. Множество точек пространства, в которых функция трех переменных f(x, y, z) принимает
одно и то же значение, f(x, y, z) = c, называется поверхностью уровня.
Слайд 28
Слайд 29

§ 3. Предел и непрерывность функции нескольких переменных
Слайд 30

Опр. Число A называется пределом функции z = f(x, y) в точке M0(x0, y0), если
для каждого числа ε > 0 найдется такое число δ = δ(ε), что при 0 < |x – x0| < δ и 0 < |y – y0| < δ выполняется неравенство |f(x,y) – A| < ε. При этом пишут
Слайд 31

Опр. Функция z = f(x, y) называется непрерывной в точке M0(x0, y0), если функция z = f(x, y)
определена в этой точке и существует
Слайд 32

Аналогичные определения имеют место и для функции u = f(x1, x2, …, xn) в случае произвольного
числа n переменных.
Слайд 33

Если в какой – либо точке условие непрерывности не выполняется, то
эта точка называется точкой разрыва функции f(x, y). Это может быть в следующих случаях:
Слайд 34

1. Функция z = f(x, y) не определена в точке M0(x0, y0).
2. Не существует предел
3. Этот предел существует, но он не равен f(x0, y0).
Слайд 35

§ 4. Частные производные функции нескольких переменных
Слайд 36
Слайд 37
Слайд 38
Слайд 39
Слайд 40
Слайд 41
Слайд 42
Слайд 43
Слайд 44
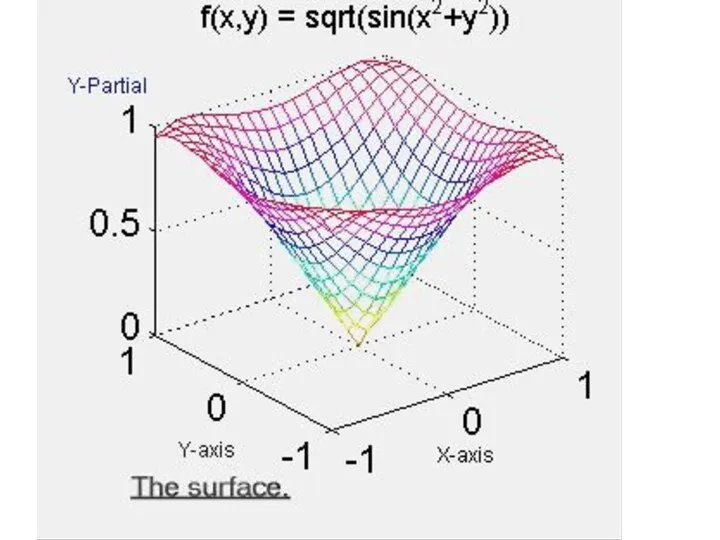
Слайд 45

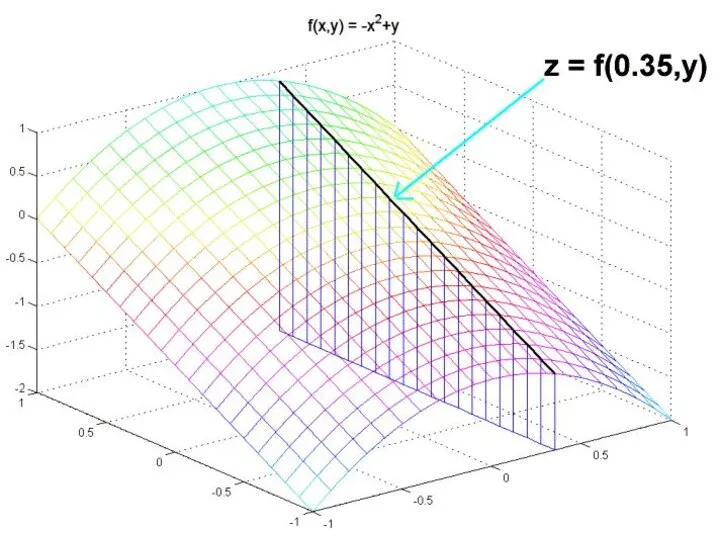
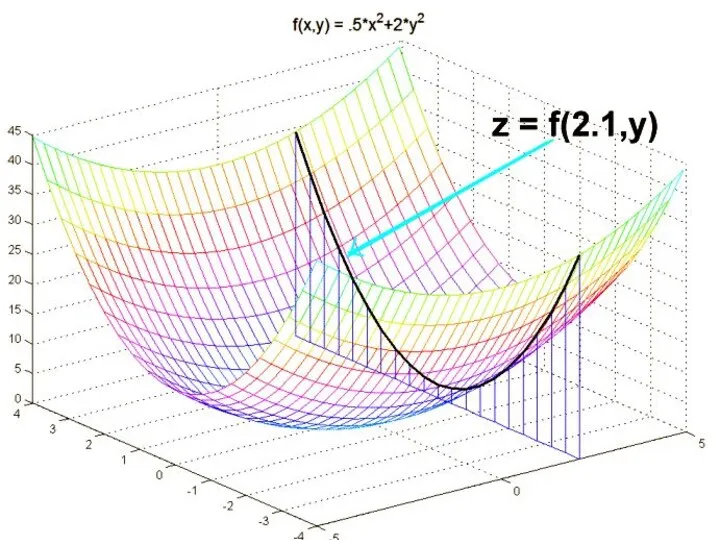
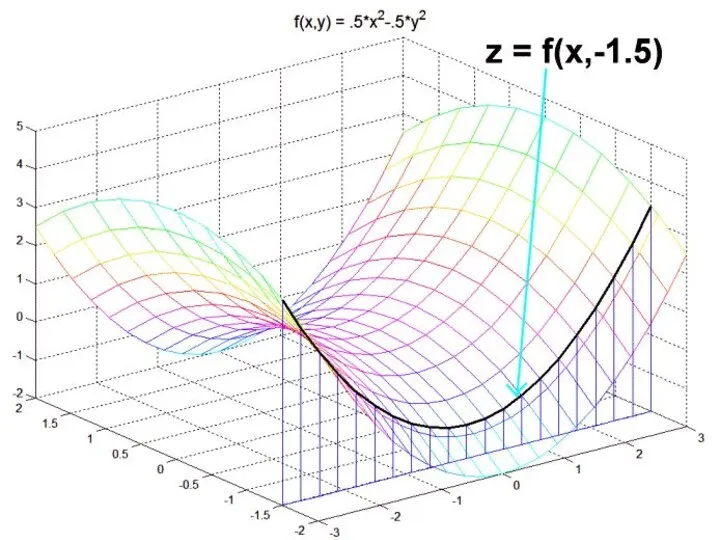
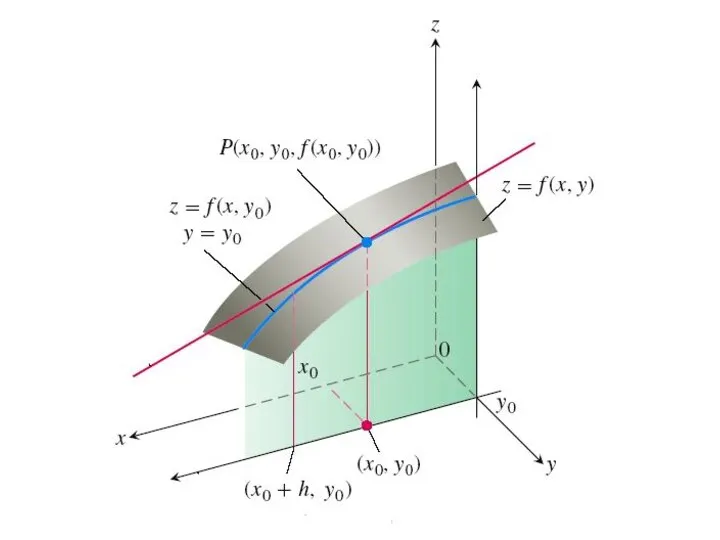
Пусть z = f(x, y) – функция двух переменных. Дадим независимой переменной x приращение
Δx, оставляя при этом переменную y неизменной. Тогда функция z получит приращение
которое называется частным приращением z по x.
Слайд 46

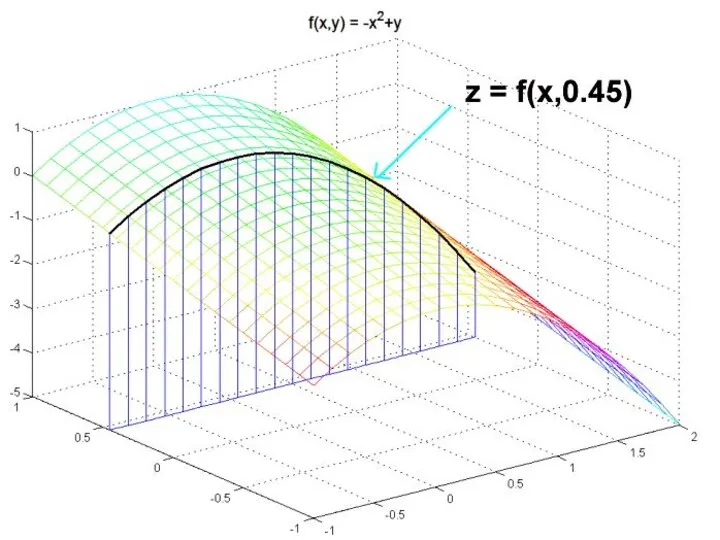
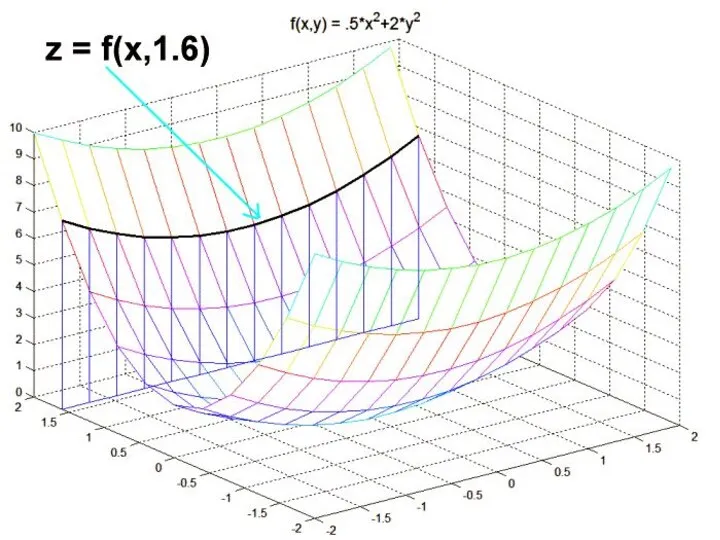
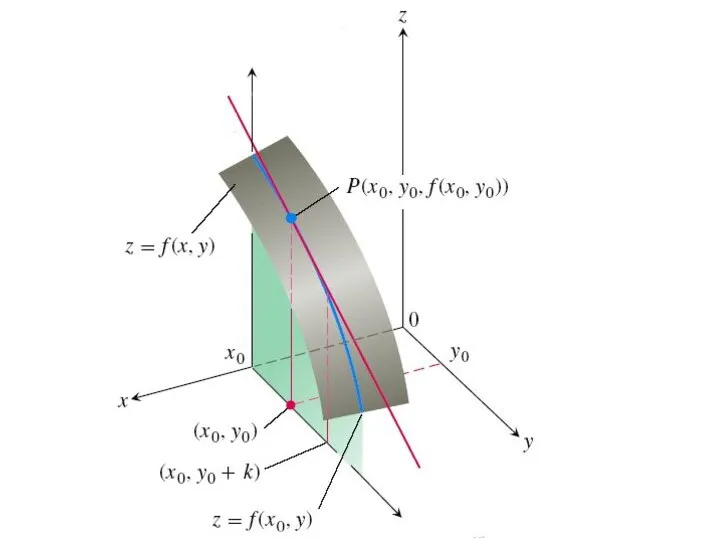
Аналогично, если независимой переменной y дадим приращение Δy, оставляя при этом
неизменной переменную x, то функция z получит приращение
называемое частным приращением z по y.
Слайд 47

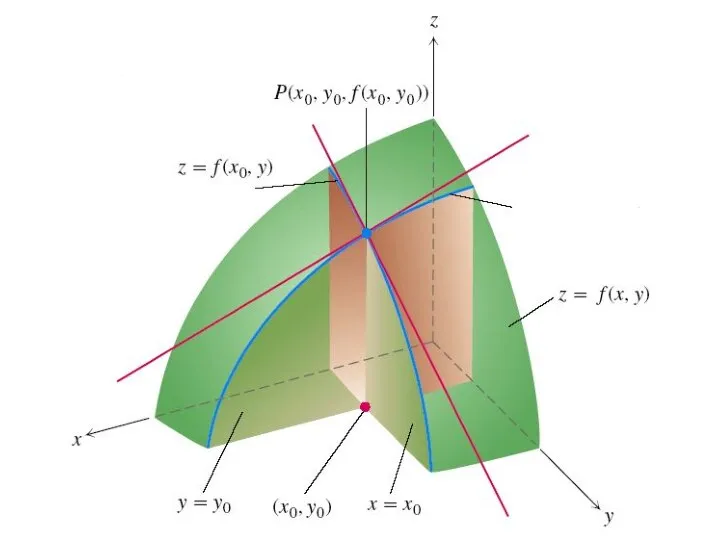
Опр. Частной производной по x от функции z называется предел отношения
частного приращения Δxz к приращению Δx при стремлении Δx к нулю.
Эта производная обозначается одним из символов
Слайд 48

Таким образом, по определению,
Слайд 49

Аналогично определяется частная производная от функ-ции z = f(x, y) по переменной y :
Обозначается
одним из символов
Слайд 50

В общем случае частной производной первого порядка функции u = f(x1, x2, …, xn) по переменной
xk называется предел
Слайд 51

Т.к. при вычислении частных производных все переменные, кроме одной, считают постоянными,
то для частных производных сохранаяются все правила и формулы дифференцирования функции одной переменной.
Слайд 52

Пример. Найти частные производные функции
Слайд 53

Решение. Полагая y = const, находим
Слайд 54
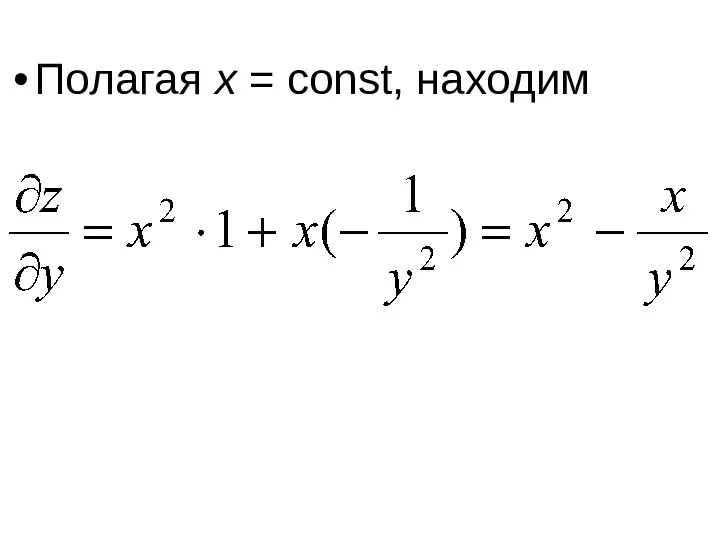
Полагая x = const, находим
Слайд 55

Пример. Найти значения частных производных функции
в точке M(1, –1, 0).
Слайд 56

Решение. Полагая y = const, z = const, находим
Слайд 57
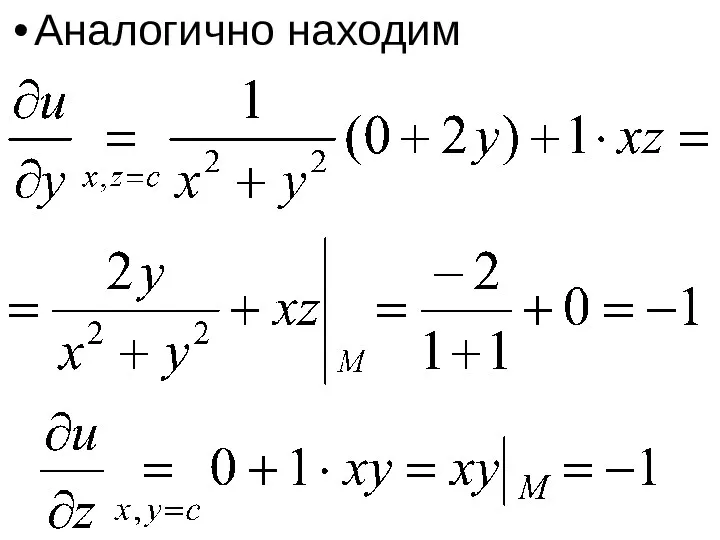
Слайд 58

Предположим, что функция z = f(x, y) имеет непрерывные частные производные
Слайд 59

Эти производные в свою очередь являются функциями независимых переменных x и
y. Будем называть
и частными производными 1-го порядка.
Слайд 60

Частными производными 2-го порядка называются частные производные от частных производных 1-го
порядка.
Для функции z = f(x, y) двух переменных можно найти четыре частные производные 2-го порядка, которые обозна-чаются следующим обр-м:
Слайд 61

Слайд 62

В общем случае смешанные частные производные могут не совпадать, однако для
них справедлива теорема:
Теорема. Если смешанные частные производные и непрерывны в некоторой точке M(x, y), то они равны, т. е.
Слайд 63

Частными производными n–го порядка называются частные производные от частных производных (n – 1)–го
порядка.
Их обозначают
и т. д.
Слайд 64

Частные производные любого порядка, взятые по различным переменным, называются смешанными.
Слайд 65

Пример. Найти частные производные 2-го порядка функции
Слайд 66

Решение. Последовательно находим
Слайд 67
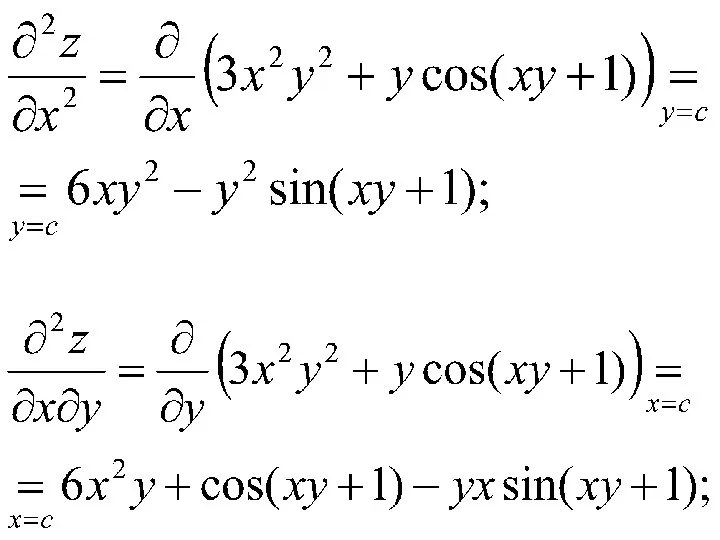
Слайд 68
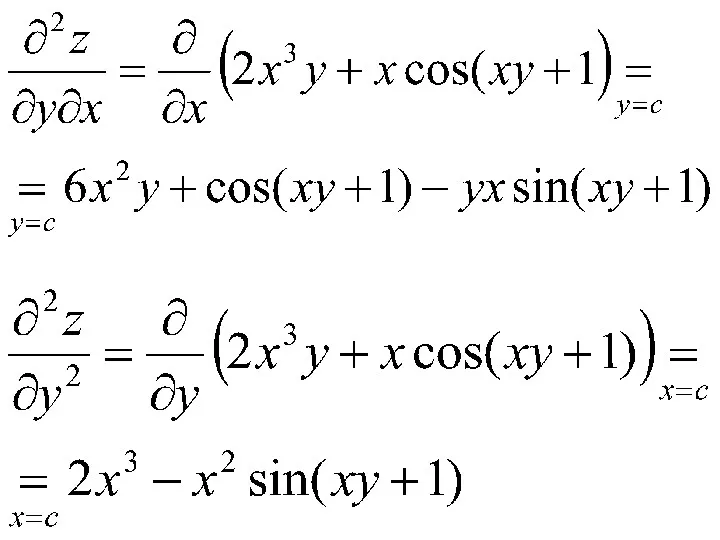
Слайд 69

Слайд 70

Слайд 71




















































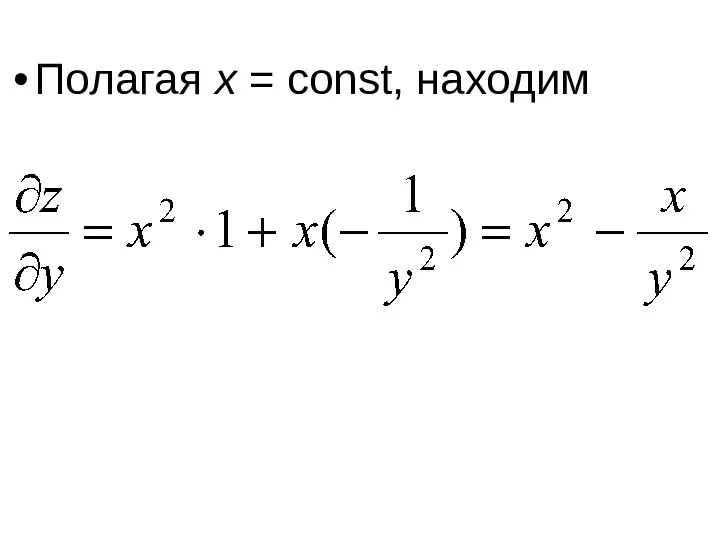


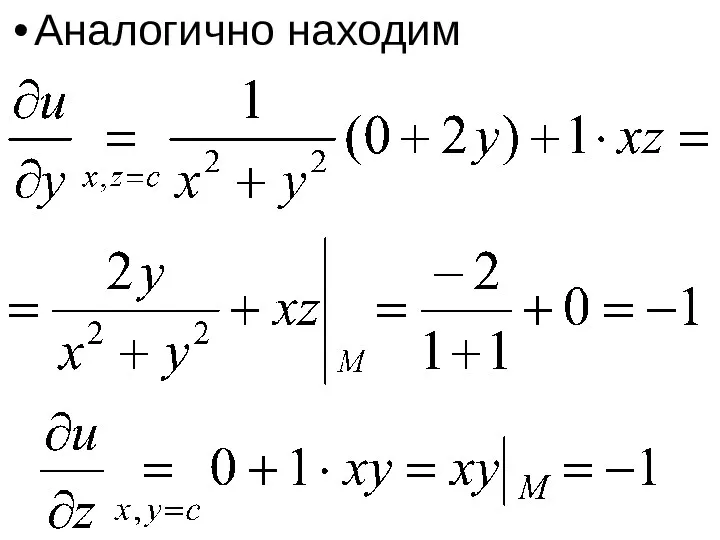









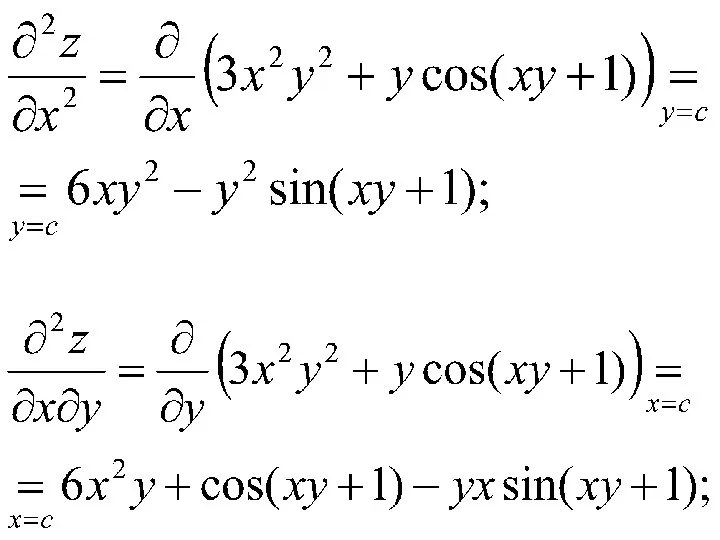
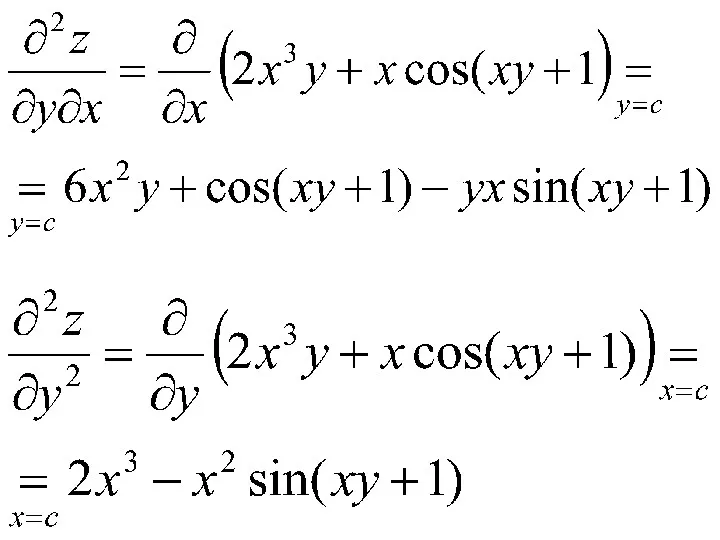



 Задачі на визначення, на скільки коротший. Обчислення значень виразів
Задачі на визначення, на скільки коротший. Обчислення значень виразів Умножение многочлена на многочлен. Алгебра 7 класс
Умножение многочлена на многочлен. Алгебра 7 класс Интегрирование по частям в определенном интеграле. Замена переменных при вычислении определенного интеграла. (Семинар 18)
Интегрирование по частям в определенном интеграле. Замена переменных при вычислении определенного интеграла. (Семинар 18) Математика+Габдулла Тукай
Математика+Габдулла Тукай Математический диктант
Математический диктант Перпендикулярность прямых и плоскостей
Перпендикулярность прямых и плоскостей Знаходження невідомого зменшуваного
Знаходження невідомого зменшуваного Величины. Объем. Литр
Величины. Объем. Литр Выпуклый анализ. Выпуклые функции.. Лекция 12
Выпуклый анализ. Выпуклые функции.. Лекция 12 Задачи мудрой совы (4 класс)
Задачи мудрой совы (4 класс) Классическое определение вероятности
Классическое определение вероятности Решение задач на проценты с помощью пропорций
Решение задач на проценты с помощью пропорций Урок 10. Случайные величины. Дискретные и непрерывные случайные величины (ДСВ и НСВ)
Урок 10. Случайные величины. Дискретные и непрерывные случайные величины (ДСВ и НСВ) Формулы сокращенного умножения
Формулы сокращенного умножения Решение Уравнений.. 6 класс
Решение Уравнений.. 6 класс Задачи на готовых чертежах. Первый признак равенства треугольников
Задачи на готовых чертежах. Первый признак равенства треугольников Умножение круглых чисел
Умножение круглых чисел Дидактическая игра Спрячь мышку
Дидактическая игра Спрячь мышку Задачі на дві дії різного ступеня: множення і додавання або віднімання (2 клас)
Задачі на дві дії різного ступеня: множення і додавання або віднімання (2 клас) Письмове ділення на одноцифрове число. Знаходження частини числа. Задачі на знаходження частини числа
Письмове ділення на одноцифрове число. Знаходження частини числа. Задачі на знаходження частини числа Умножение десятичной дроби на натуральное число. Урок математики в 5 классе
Умножение десятичной дроби на натуральное число. Урок математики в 5 классе Задачи на деление
Задачи на деление Вычитание вида 11-
Вычитание вида 11- synus_kosynus_tangens_gostrogo_kuta_pryamokutnogo_trykutnyka
synus_kosynus_tangens_gostrogo_kuta_pryamokutnogo_trykutnyka ЕГЭ - 2017 по математике. Базовый уровень. Задачи на логику и смекалку
ЕГЭ - 2017 по математике. Базовый уровень. Задачи на логику и смекалку Электронный тренажёр по математике для учащихся 1 класса. Тема: Материал для повторения и самоконтроля. ОС Перспектива
Электронный тренажёр по математике для учащихся 1 класса. Тема: Материал для повторения и самоконтроля. ОС Перспектива конспект по ФЭМП В гости к бабушке для второй младшей группы
конспект по ФЭМП В гости к бабушке для второй младшей группы Геометрия. 7 класс. Измерение отрезков и углов
Геометрия. 7 класс. Измерение отрезков и углов