Содержание
- 2. 3. ВЫПУКЛЫЕ ФУНКЦИИ (ПРОДОЛЖЕНИЕ) 3.4. Дифференцируемость выпуклой функции по всем возможным направлениям. 3.3. Непрерывность выпуклой функции.
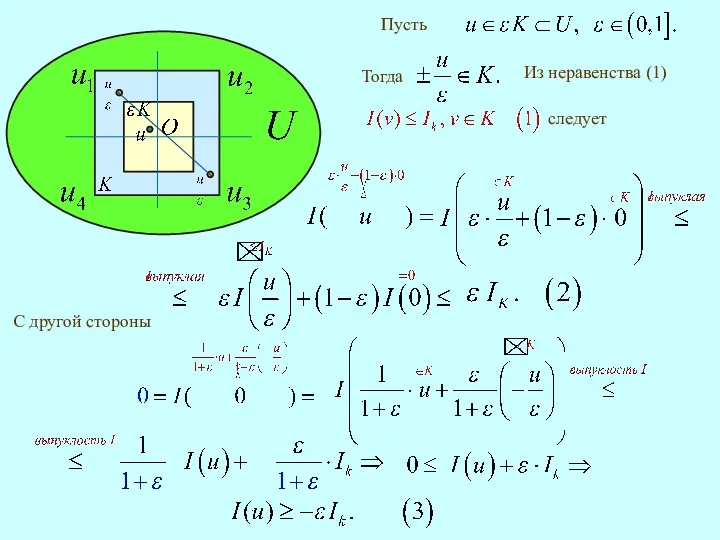
- 3. 3.3. Непрерывность выпуклой функции. оказывается столь сильным, Теорема 6. выпукла. Доказательство. Сначала предположим, что с центром
- 4. Из неравенства (1) следует С другой стороны
- 5. Общий случай сводится к уже рассмотренному определенной формулой Тогда по доказанному она непрерывна в нуле. Непрерывной
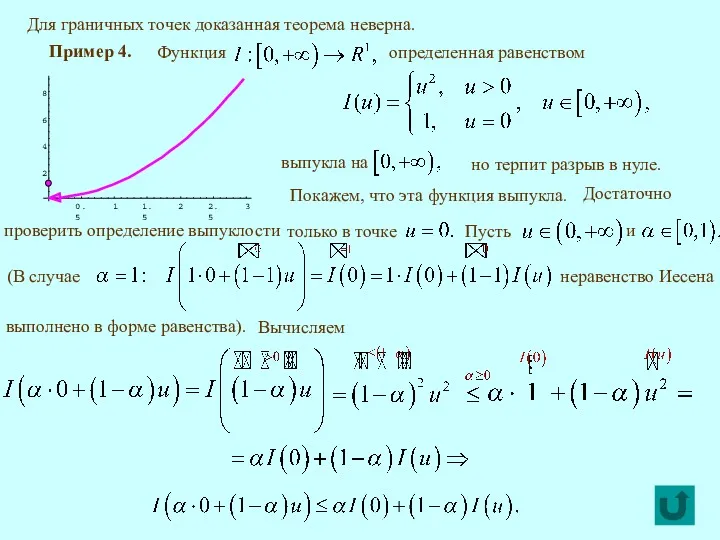
- 6. Для граничных точек доказанная теорема неверна. Пример 4. но терпит разрыв в нуле. Покажем, что эта
- 7. 3.4. Дифференцируемость выпуклой функции по всем возможным направлениям. Определение 3. такое, что Пример 5. Пример 6.
- 8. Пример 7. имеется хотя бы одно возможное направление. и содержит не менее двух точек. Определение 4.
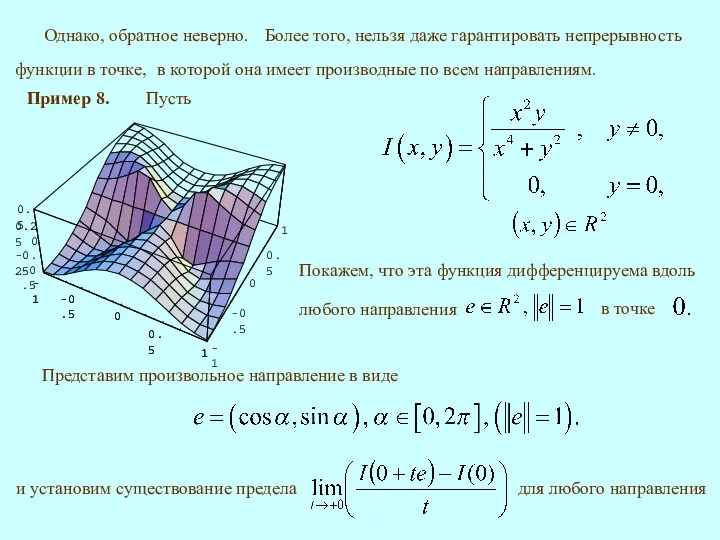
- 9. в которой она имеет производные по всем направлениям. Пример 8. Пусть Однако, обратное неверно. Представим произвольное
- 10. Отсюда выводим Таким образом, указанный предел существует.
- 11. Тогда Теорема 7. выпукла. Доказательство. Имеет место включение С другой стороны
- 12. Тогда
- 13. Имеет место равенство Тогда
- 15. Упражнение 1. Решение. Функция нормы выпукла и конечна.
- 17. Скачать презентацию







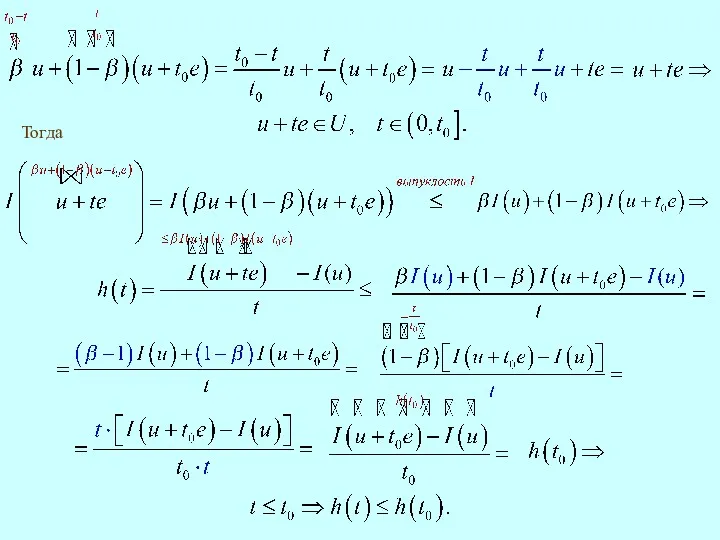



 Дидактическая игра Спрячь мышку
Дидактическая игра Спрячь мышку Планиметрия в вопросах и ответах
Планиметрия в вопросах и ответах Пропорция. Урок – обобщение
Пропорция. Урок – обобщение Умножение и деление десятичных дробей
Умножение и деление десятичных дробей Решение задач на нахождение дроби от числа
Решение задач на нахождение дроби от числа Дисциплина Физика, математика
Дисциплина Физика, математика Обзор распространенных тестов зависимость и независимость выборок (не-) и параметрические и тесты корреляции
Обзор распространенных тестов зависимость и независимость выборок (не-) и параметрические и тесты корреляции Действия с дробями. Умножение дробей
Действия с дробями. Умножение дробей Треугольники. Элементы треугольника, равнобедренный треугольник, сумма углов треугольника. Повторение, подготовка к ГИА
Треугольники. Элементы треугольника, равнобедренный треугольник, сумма углов треугольника. Повторение, подготовка к ГИА Деление и умножение трехзначных чисел (устные вычисления).
Деление и умножение трехзначных чисел (устные вычисления). урок по математике Письменное сложение трехзначных чисел
урок по математике Письменное сложение трехзначных чисел Связь между компонентами и результатом умножения
Связь между компонентами и результатом умножения Таблица умножения двух (тренажёр)
Таблица умножения двух (тренажёр) Обобщение материала по теме Умножение и деление обыкновенных дробей 6 класс
Обобщение материала по теме Умножение и деление обыкновенных дробей 6 класс Измерение длины отрезка. Вопросы, упражнение
Измерение длины отрезка. Вопросы, упражнение Урок математики в 1 классе по теме Сравнение с нулём
Урок математики в 1 классе по теме Сравнение с нулём Исследование функций и построение графиков с помощью производной
Исследование функций и построение графиков с помощью производной Четырехугольники. Подготовка к ОГЭ
Четырехугольники. Подготовка к ОГЭ Тренажёр. Считаем с ёжиком
Тренажёр. Считаем с ёжиком Решение задач по темам Нахождение числа по его дроби, Нахождение дроби от числа
Решение задач по темам Нахождение числа по его дроби, Нахождение дроби от числа Презентация Прямоугольник, квадрат
Презентация Прямоугольник, квадрат Признаки делимости на 2; 3; 5; 9; 10
Признаки делимости на 2; 3; 5; 9; 10 Решение неравенств второй степени. Подготовка к ГИА. 9 класс
Решение неравенств второй степени. Подготовка к ГИА. 9 класс Логарифмическая функция, её свойства и график
Логарифмическая функция, её свойства и график Ознакомление с задачей в 2 действия
Ознакомление с задачей в 2 действия Урок математики. Тема Неравенство
Урок математики. Тема Неравенство конспект урока и презентация к уроку математики во 2 классе
конспект урока и презентация к уроку математики во 2 классе Задача с двумя переменными. Урок математики 1 класс
Задача с двумя переменными. Урок математики 1 класс