Содержание
- 2. Определение 1: Обыкновенным дифференциальным уравнением n-ого порядка называется уравнение вида где, y = y(x) искомая функция.
- 3. Определение 3: Если решение данного уравнения задано в неявном виде Ф(x,y)=0, то оно называется интегралом уравнения
- 4. Таким образом, общее решение уравнения (1) представляет собой семество функций, которое имеет вид y = (2).
- 5. Определение 6: Дифференциальным уравнением первого порядка называется уравнение (4). Определение 7: Если уравнение (4) удается привести
- 6. Определение: Общим решением дифференциального уравнения первого порядка = f(x,y) в области D, называется функция , обладающая
- 7. Определение: Всякое решение , получающееся из общего решения , при конкретном C= называется частным решением. Определение
- 8. Однако встречаются дифференциальные уравнения, имеющие также решения, которые не получаются из общего ни при каких значениях
- 9. Определение: Дано дифференциальное уравнение F(x,y, )=0. Пусть его можно переписать в виде (5) Если уравнение (5)
- 10. Метод решения: | : ≠0 | : ≠0 Интегрируя обе части, получаем общий интеграл уравнения.
- 11. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.
- 12. Определение: Дифференциальные уравнения первого порядка вида a(x)y’+ +b(x)y+c(x)=0,где a,b,c – заданные функции, называется линейным дифференциальным уравнением
- 13. Определение: Если , то линейное уравнение называется неоднородным. y’+p(x)y=f(x) Определение: Если , то уравнение y'+p(x)y=0 называется
- 14. Решение методом Бернулли y ищем в виде произведения функции и , т.е. Найдем одну функцию такую,
- 15. (так как v ≠0); Уравнение с разделяющимися переменными:
- 16. Особых решений нет. Уравнение с разделяющимися переменными. Общее решение:
- 17. Определение: Дифференциальное уравнение первого порядка вида называется уравнением Бернулли. Метод решения: с помощью подстановки уравнение Бернулли
- 18. Дано: уравнение первого порядка вида y’+p(x)*y=f(x) Алгоритм решения. Рассмотрим соответствующее однородное уравнение . Найдем его решение.
- 19. Варьируем произвольную постоянную. Пусть . Найдем функцию из условия, что функция является решением неоднородного дифференциального уравнения.
- 20. + Общее решение:
- 21. Определение: Функция f(x,y) называется однородной измерения m, если для любой . Определение: Уравнение вида называется однородным,
- 22. Теорема 1: Однородные дифференциальные уравнения первого порядка сводится к уравнению первого порядка с разделёнными переменными c
- 23. Теорема 2: Дифференциальное уравнение y’=f(x,y) является однородным тогда и только тогда, когда f(x,y) есть однородная функция
- 24. Теорема существования и единственности решения. Особые решения.
- 25. Если в дифференциальном уравнении функция непрерывна в некоторой области D плоскости Oxy и имеет в этой
- 26. Определение: Точки области D, в котором нарушается единственность решения задачи Коши, называется особыми точками дифференциального уравнения.
- 27. Графиком особого решения является огибающая семейства интегральных кривых, она находится путем исключения, если это возможно, параметра
- 28. Теорема существования и единственности решения задачи Коши для дифференциальных уравнения высших порядков
- 29. Определение: . Определение: Задачей Коши для дифференциальных уравнений: называется задача отыскания решения y=y(x), удовлетворяющего заданным начальным
- 30. Определение: Общим решением уравнения называется такая функция , которая при любых допустимых значениях параметров , является
- 32. Скачать презентацию





























 Прямой параллелепипед
Прямой параллелепипед Транспортная задача. (Лекции 10,11)
Транспортная задача. (Лекции 10,11) Теорема Пифагора
Теорема Пифагора Перпендикулярность плоскостей. Параллелепипед
Перпендикулярность плоскостей. Параллелепипед Представление числовой информации в таблицах. Часть 2
Представление числовой информации в таблицах. Часть 2 Вовка в математическом царстве. Часть 2
Вовка в математическом царстве. Часть 2 Решение показательных уравнений и неравенств
Решение показательных уравнений и неравенств Описанная окружность
Описанная окружность Доли. Обыкновенные дроби (математика, 5 класс)
Доли. Обыкновенные дроби (математика, 5 класс) Вероятность и статистика. Урок 2. 7 класс
Вероятность и статистика. Урок 2. 7 класс Урок математики Умножение с 0 и 1
Урок математики Умножение с 0 и 1 урок математики в 1 классе по теме Зависимость между компонентами вычитания (УМК Перспектива) Диск
урок математики в 1 классе по теме Зависимость между компонентами вычитания (УМК Перспектива) Диск Линейная функция и её график
Линейная функция и её график Математическая игра Решай! Смекай! Отгадывай!
Математическая игра Решай! Смекай! Отгадывай! Единицы измерения времени: час и минута
Единицы измерения времени: час и минута Нумерація чисел в межах 100
Нумерація чисел в межах 100 Алгоритмы на графах
Алгоритмы на графах Решение задач С2. Нахождение расстояния между двумя скрещивающимися прямыми
Решение задач С2. Нахождение расстояния между двумя скрещивающимися прямыми Объемы. Объем прямоугольного параллелепипеда
Объемы. Объем прямоугольного параллелепипеда Числа от 1 до 20. Десятичный состав чисел второго десятка.
Числа от 1 до 20. Десятичный состав чисел второго десятка. Теорема Дезарга
Теорема Дезарга Решение задач на проценты
Решение задач на проценты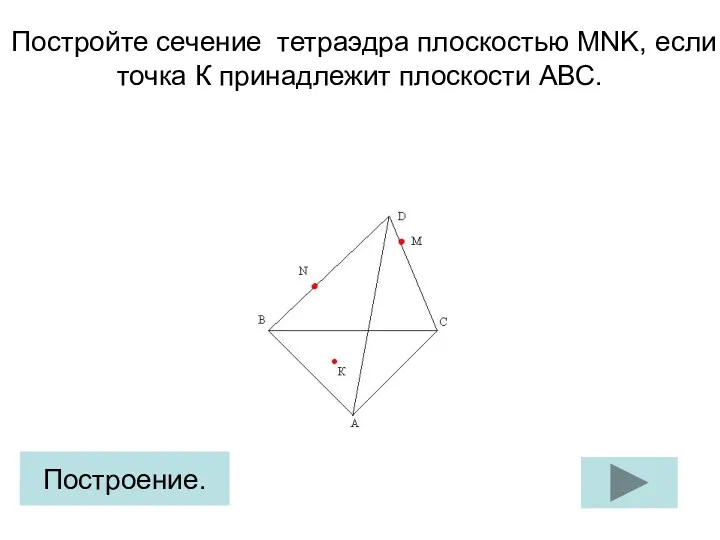 Тетраэдр. Построение сечения (задание 5)
Тетраэдр. Построение сечения (задание 5) Последовательность Фибоначчи. Парадоксы с площадью
Последовательность Фибоначчи. Парадоксы с площадью Путешествие в поисках приключений с Нэмо
Путешествие в поисках приключений с Нэмо Доказательство теоремы Пифагора
Доказательство теоремы Пифагора Прямоугольная система координат в пространстве. 11 класс
Прямоугольная система координат в пространстве. 11 класс Классическое определение вероятности события
Классическое определение вероятности события