Содержание
- 2. Определение: Дифференциальное исчисление Дифференцируемость функции где А – некоторое число; о(Δx) – бесконечно малая функция более
- 3. Теорема: Дифференциальное исчисление Дифференцируемость функции Если функция f (x) дифференцируема в точке x0 , то она
- 4. Дифференциальное исчисление Дифференциал функции Из определения дифференцируемости функции и её производной получаем, что Если то Значит,
- 5. Определение: Дифференциальное исчисление Дифференциал функции Таким образом, по определению Главная линейная часть приращения функции f (x)
- 6. Дифференциальное исчисление Дифференциал функции Рассмотрим функцию у = х. То есть, приращение и дифференциал независимой переменной
- 7. Дифференциальное исчисление Перепишем выражение для дифференциала функции в виде Пусть y = f (x) – некоторая
- 8. Дифференциальное исчисление Свойства дифференциала функции Для дифференциалов двух функций f (x) и g(x) справедливы следующие формулы:
- 9. Пример: Решение: в точке х0 = 1. Найти дифференциал функции Дифференциальное исчисление Дифференциал функции Автор: И.В.
- 10. Дифференциальное исчисление Приложения дифференциала функции С помощью дифференциала можно приближённо вычислять значения функции f (x) для
- 11. Пример: Решение: Вычислить приближённо Дифференциальное исчисление Приложения дифференциала функции Автор: И.В. Дайняк, к.т.н., доцент Кафедра высшей
- 12. Пусть f (x) – сложная дифференцируемая функция, где x = ϕ (t) – дифференцируемая функция. Дифференциальное
- 13. Дифференциал функции всегда равен произведению её производной на дифференциал аргумента и не зависит от того, является
- 15. Скачать презентацию












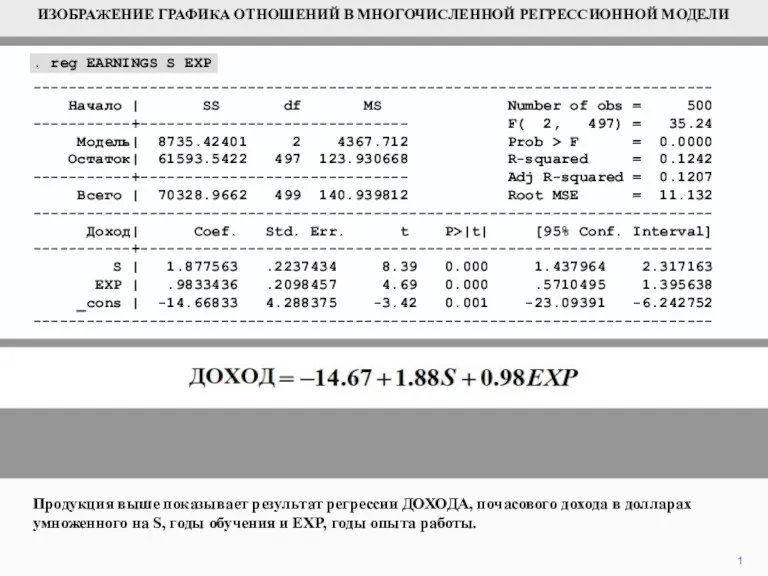 Изображение графика отношений в многочисленной регрессионной модели
Изображение графика отношений в многочисленной регрессионной модели Последовательность. Лингво–математический урок
Последовательность. Лингво–математический урок Подготовка учащихся к ОГЭ по математике
Подготовка учащихся к ОГЭ по математике Цилиндр, конус и шар
Цилиндр, конус и шар Движение по окружности
Движение по окружности Сумма углов треугольника
Сумма углов треугольника ГИА - 2012. Открытый банк заданий по математике. (Задача 4)
ГИА - 2012. Открытый банк заданий по математике. (Задача 4) Создание тренажера по подготовке к ОГЭ по математике
Создание тренажера по подготовке к ОГЭ по математике Центральные и вписанные углы
Центральные и вписанные углы Правильные многогранники
Правильные многогранники Элективный курс. Фигурные числа. (5-7 класс)
Элективный курс. Фигурные числа. (5-7 класс) Число и цифра 7.
Число и цифра 7. Активизация познавательной деятельности учащихся на уроках математики
Активизация познавательной деятельности учащихся на уроках математики Степени и корни
Степени и корни Полуплоскость. Луч. Прямая
Полуплоскость. Луч. Прямая Два замечательных предела
Два замечательных предела Рациональные неравенства. Задания для устного счета
Рациональные неравенства. Задания для устного счета Длина окружности (6 класс)
Длина окружности (6 класс)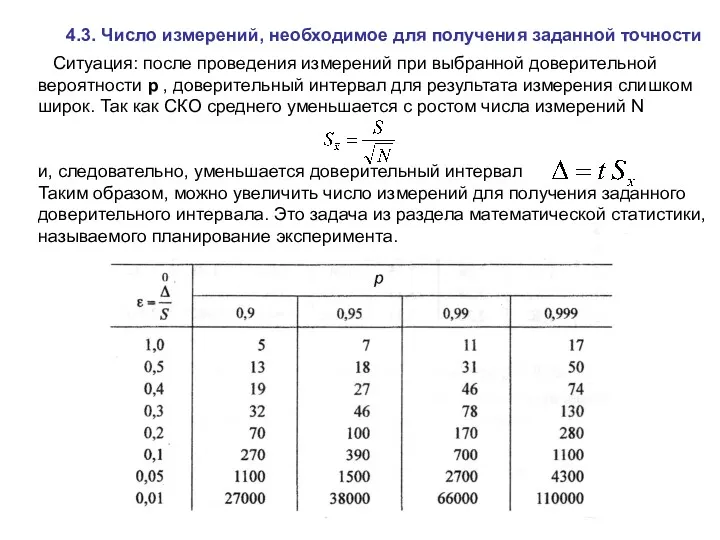 Число измерений, необходимое для получения заданной точности
Число измерений, необходимое для получения заданной точности Математическая игра Звездный час
Математическая игра Звездный час Основы математики
Основы математики The circle, the circumference and their elements. The central angle
The circle, the circumference and their elements. The central angle Положительные и отрицательные числа вокруг нас
Положительные и отрицательные числа вокруг нас Движение. Урок математики в 4 классе
Движение. Урок математики в 4 классе Обобщение по теме Четырехугольники. 8 класс
Обобщение по теме Четырехугольники. 8 класс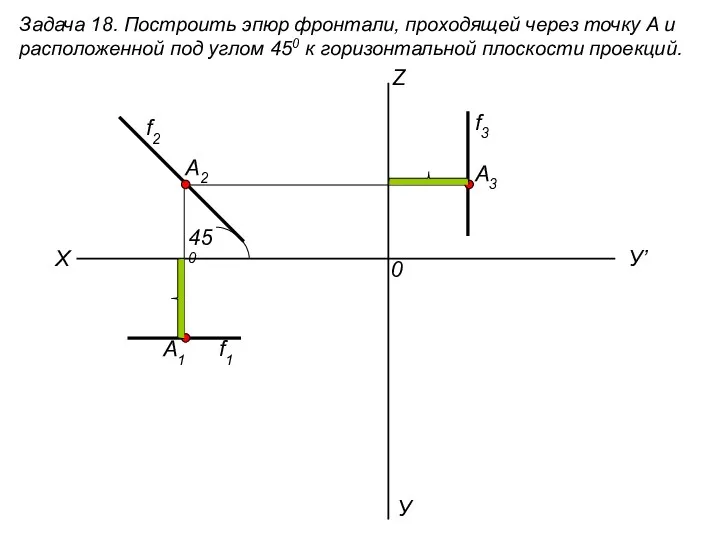 Построить эпюр фронтали, проходящей через точку А и расположенной под углом 450 к горизонтальной плоскости проекций. (задача 18)
Построить эпюр фронтали, проходящей через точку А и расположенной под углом 450 к горизонтальной плоскости проекций. (задача 18) методическая разработка урока математики Единицы времени.Век
методическая разработка урока математики Единицы времени.Век Статистические методы проверки гипотез
Статистические методы проверки гипотез