Содержание
- 2. Дискретная математика Дискре́тная матема́тика — область математики, занимающаяся изучением дискретных структур, которые возникают как в пределах
- 3. История развития Возникновение дискретной математики относят к глубокой древности. С незапамятных времен известны комбинаторно-логические задачи, решение
- 4. История развития Широко известны изобретенные в древности различные системы представления чисел, включая позиционную, и связанные с
- 5. Темы в дискретной математике Теоретическая информатика Теоретическая информатика включает области дискретной математики, относящейся к вычислению. Это
- 6. Информационная теория Информационная теория включает определение количества информации. Тесно связанный кодирует теорию, которая используется, чтобы проектировать
- 7. Логика Логика - исследование принципов действительного рассуждения и вывода, а также последовательности, разумности и полноты. Например,
- 8. Логические формулы - дискретные структуры, как доказательства, которые формируют конечные деревья или, более широко, направили нециклические
- 9. Теория множеств Теория множеств - отрасль математики, которая изучает наборы, которые являются коллекциями объектов, такой как
- 10. Комбинаторика Комбинаторика изучает путь, которым дискретные структуры могут быть объединены или устроены. Исчисляющие концентраты комбинаторики при
- 11. Теория графов Теорию графов, исследование графов и сетей, часто считают частью комбинаторики, но стала достаточно большой
- 12. Вероятность Дискретная теория вероятности имеет дело с событиями, которые происходят в исчисляемых типовых местах. Например, наблюдения
- 13. Теория чисел Теория чисел касается свойств чисел в целом, особенно целые числа. У этого есть применения
- 14. Алгебра Алгеброические структуры происходят и как дискретные примеры и как непрерывные примеры. Дискретная алгебра включает: булева
- 15. Исчисление конечных разностей, дискретное исчисление или дискретный анализ Функция, определенная на интервале целых чисел, обычно вызывается
- 16. Геометрия Дискретная геометрия и комбинаторная геометрия о комбинаторных свойствах дискретных коллекций геометрических объектов. Давняя тема в
- 17. Топология Хотя топология - область математики, которая формализует и обобщает интуитивное понятие «непрерывной деформации» объектов, это
- 18. Операционное исследование Операционное исследование обеспечивает методы для решения практических проблем в бизнесе и других областях —
- 19. Теория игр, теория решения, сервисная теория, социальная теория выбора Теория решения касается идентификации ценностей, неуверенности и
- 20. Дискретизация Дискретизация касается процесса передачи непрерывных моделей и уравнений в дискретные копии, часто в целях сделать
- 21. Дискретные аналоги непрерывной математики Есть много понятий в непрерывной математике, у которых есть дискретные версии, такие
- 22. Гибридная дискретная и непрерывная математика Исчисление временных рамок - объединение теории разностных уравнений с тем из
- 23. Вывод Сегодня дискретная математика является не только фундаментом математической кибернетики, но и важным звеном математического образования.
- 24. Основные свойства операций
- 27. Контрольная работа № 2 ВЫУЧИТЬ НАИЗУСТЬ ОСНОВНЫЕ СВОЙСТВА ОПЕРАЦИЙ (ЗАДАНИЕ НА ЭКЗАМЕНЕ) ДОКАЗАТЬ, ДИСТРИБУТИВНОСТЬ ОТНОСИТЕЛЬНО ПЕРЕСЕЧЕНИЯ
- 28. Relation(Отношение) - R -R – ЭТО МНОЖЕСТВО ОБОЗНАЧАЕТ ОТНОШЕНИЕ МЕЖДУ ЭЛЕМЕНТАМИ R
- 29. АxB-прямое произведение множеств A={a,s,d,f}-располагается на оси абцисс (ось 1) B={q,w,e,r}-располагается на оси ординат (ось 2) B
- 30. АxB-прямое произведение множеств AxB={{a,q},{a,w},{a,e},{a,r}, {s,q},{s,w},{s,e},{s,r}, {d,q},{d,w},{d,e},{d,r}, {f,q},{f,w},{f,e},{f,r} |AxB|=16 B A Ось 2 Ось 1
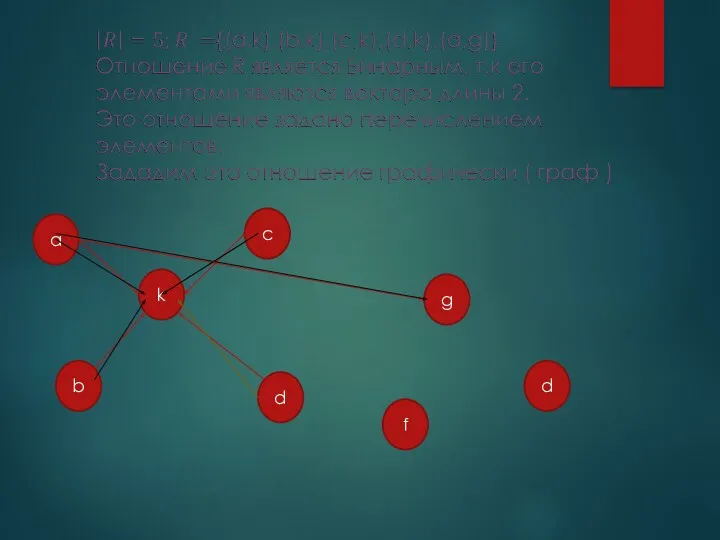
- 31. Бинарное отношение B A Ось 2 Ось 1
- 32. a b k d c f d g
- 33. Бинарное отношение R можно задать так-же таблицей (Матрицей) множество из оси 1 располагается Вертикально множество из
- 34. R; AxB AxB R AxB R
- 35. Свойства Отношений a R a b a b a b c R R R
- 36. Свойства Отношений a R a b a b a b c R R R
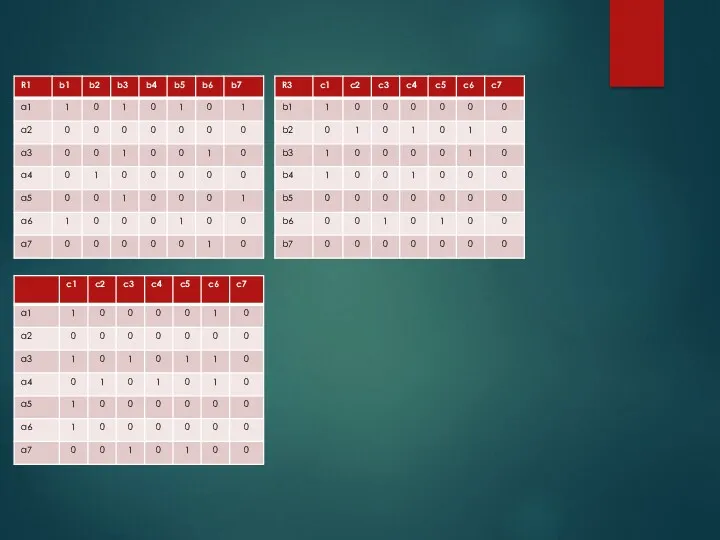
- 37. ПРЕДСТАВИМ ДАННЫЕ ОТНОШЕНИЯ С ПОМОЩЬЮ МАТРИЦЫ В данной матрице по диагонали будут располагаться 1 Также матрица
- 38. 2 1 3
- 40. Пересечение
- 41. Объединение
- 42. Дополнение
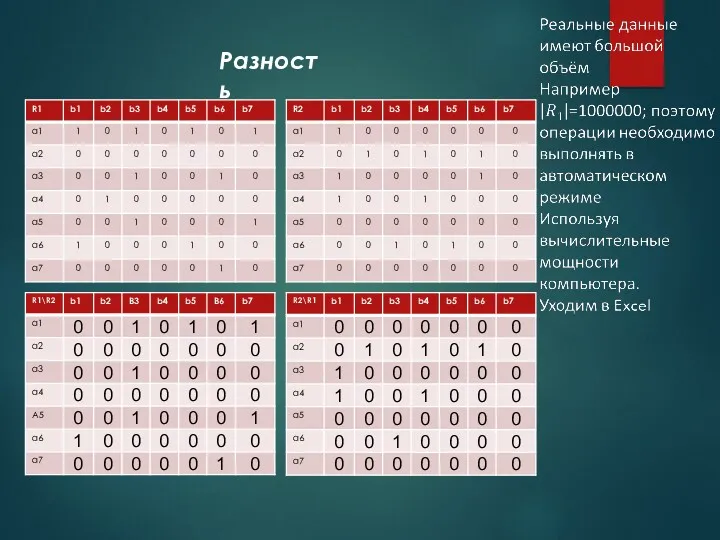
- 43. Разность
- 44. Симметрическая разность R1 R2
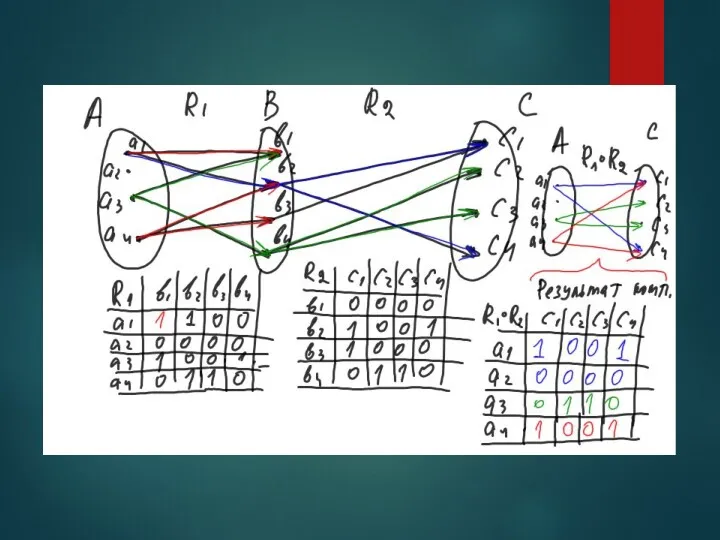
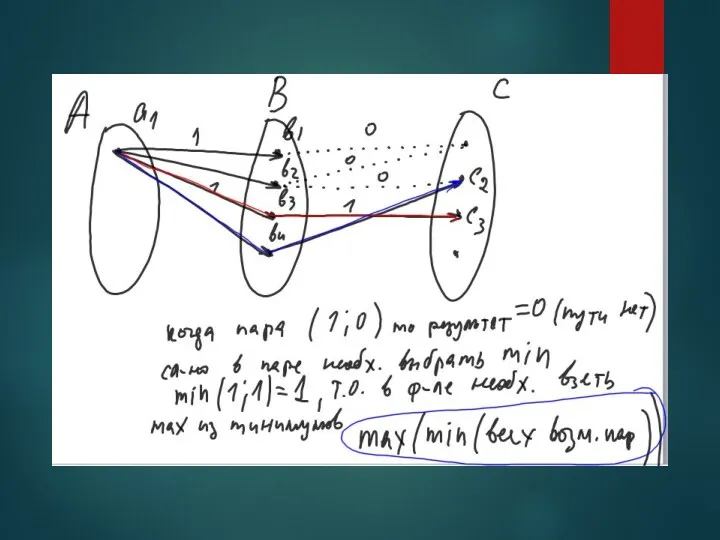
- 46. Композиция отношений ПОЗВОЛЯЕТ ВЫПОЛНИТЬ ПЕРЕХОД ИЗ ОДНОГО УНИВЕРСУМА В ДРУГОЙ ДЛЯ ЭТОГО ПЕРЕХОДА НЕОБХОДИМО ИМЕТЬ ОБЩЕЕ
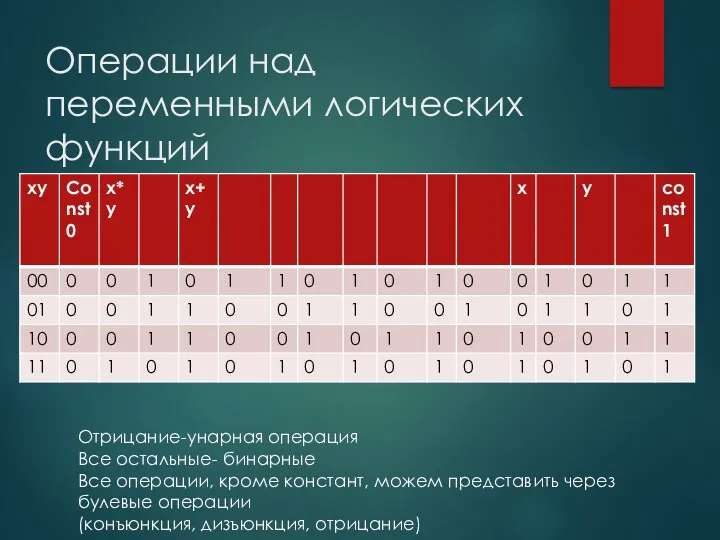
- 53. Операции над переменными логических функций Любую операцию в булевом базисе. Булевый базис(3 операции:К,Д,И)
- 54. Операции над переменными логических функций Отрицание-унарная операция Все остальные- бинарные Все операции, кроме констант, можем представить
- 55. Таблицы истинности ,через булео базис
- 56. 1 дизъюнкция
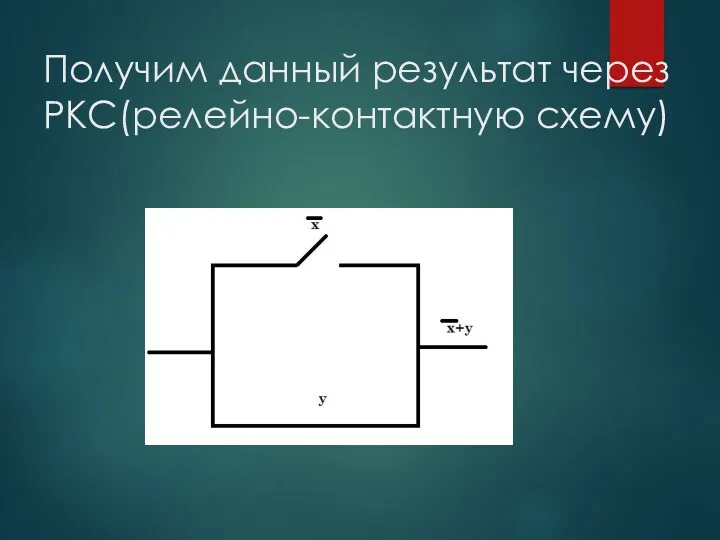
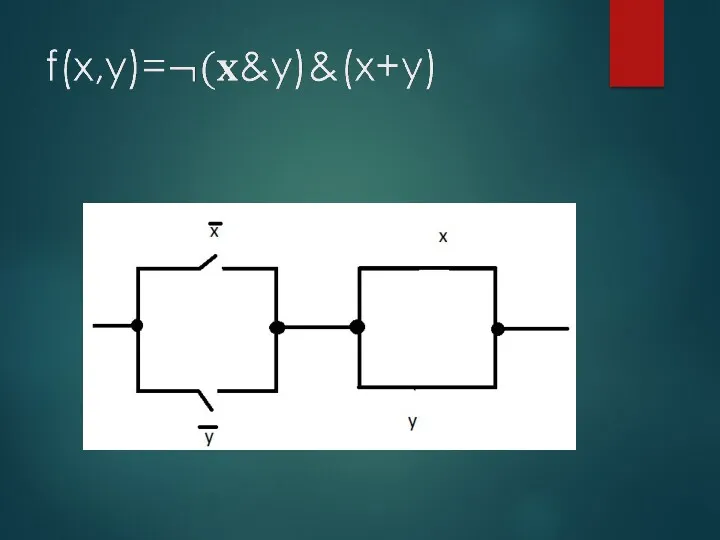
- 57. Получим данный результат через РКС(релейно-контактную схему)
- 58. Булевый базис реализуется Логические элементы:
- 59. Логические элементы в Цифровых вычислительных системах
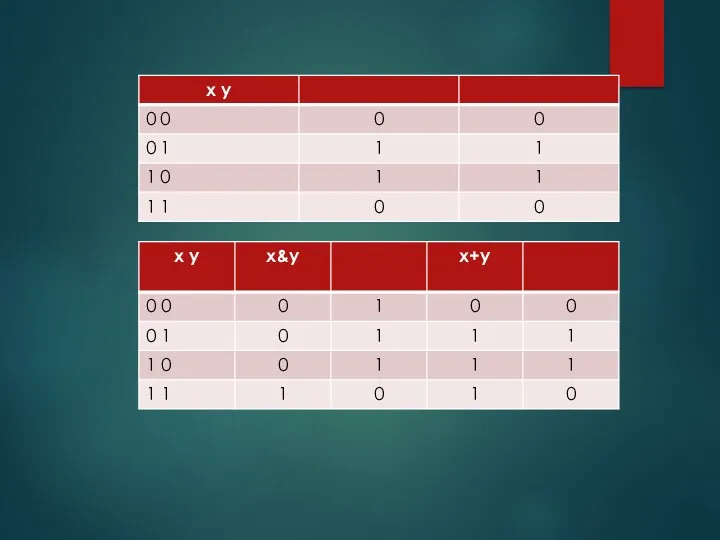
- 60. Булевый базис реализуемый с помощью РКС x x&y x x+y y y
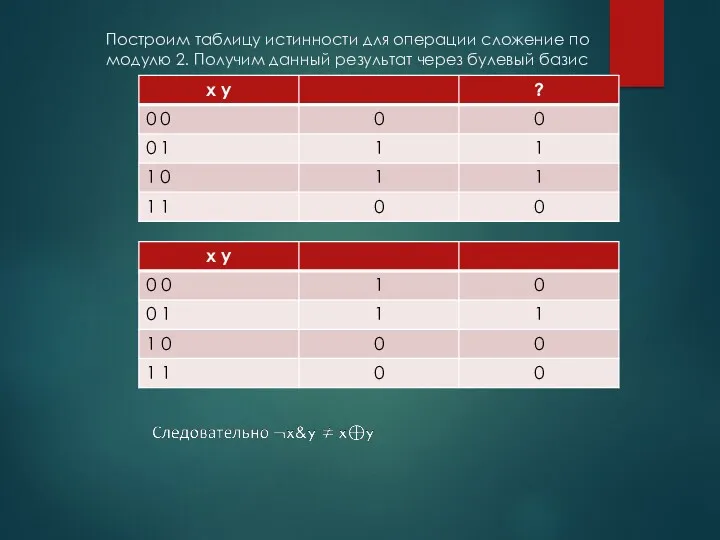
- 61. Построим таблицу истинности для операции сложение по модулю 2. Получим данный результат через булевый базис
- 63. Домашнее задание
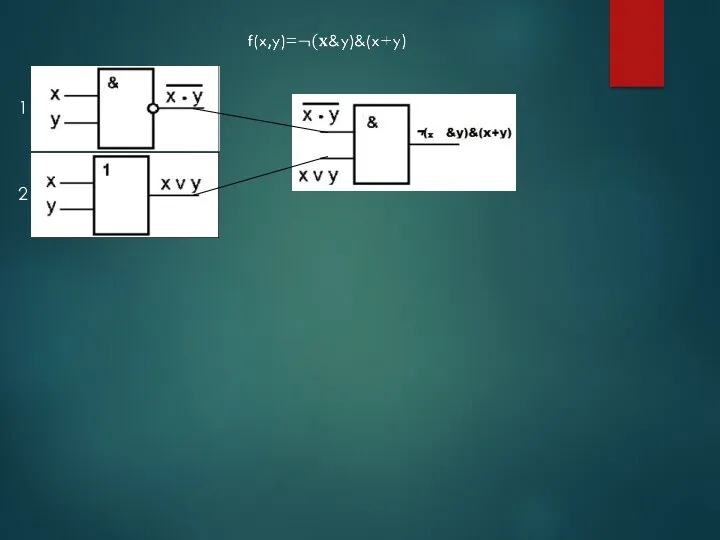
- 65. 1 2
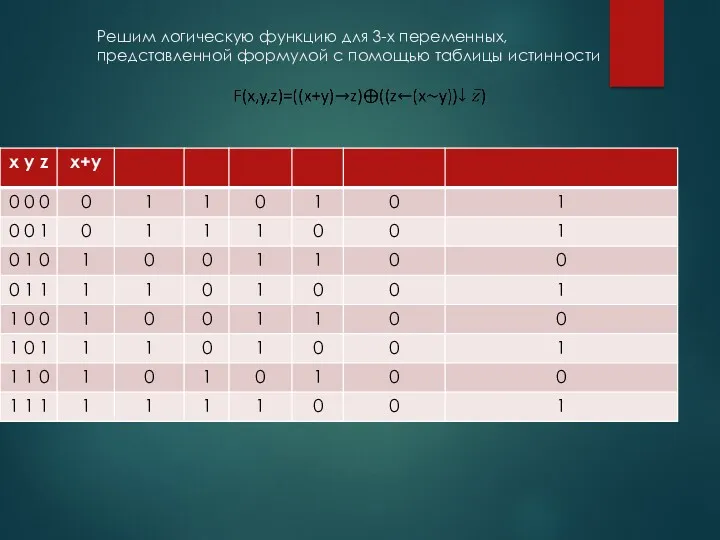
- 69. Решим логическую функцию для 3-х переменных, представленной формулой с помощью таблицы истинности +
- 70. Решим логическую функцию для 3-х переменных, представленной формулой с помощью таблицы истинности
- 71. Д/з. Лог. Формулу с помощью таблицы истинности .
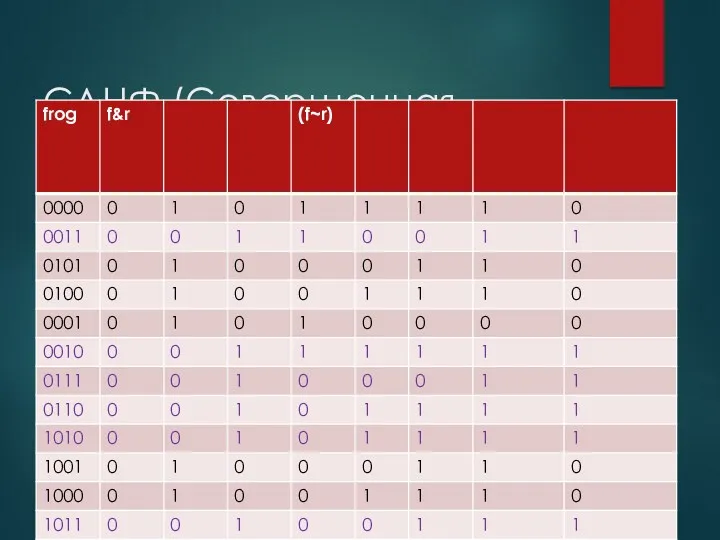
- 72. Домашнее задание Решить логическую формулу с помощью таблицы истинности для f(f,r,o,g)=
- 75. СДНФ (Совершенная дизъюнктивная нормальная форма)
- 76. СДНФ (Совершенная дизъюнктивная нормальная форма) С помощью СДНФ мы можем представить результат полученный в таблице истинности.
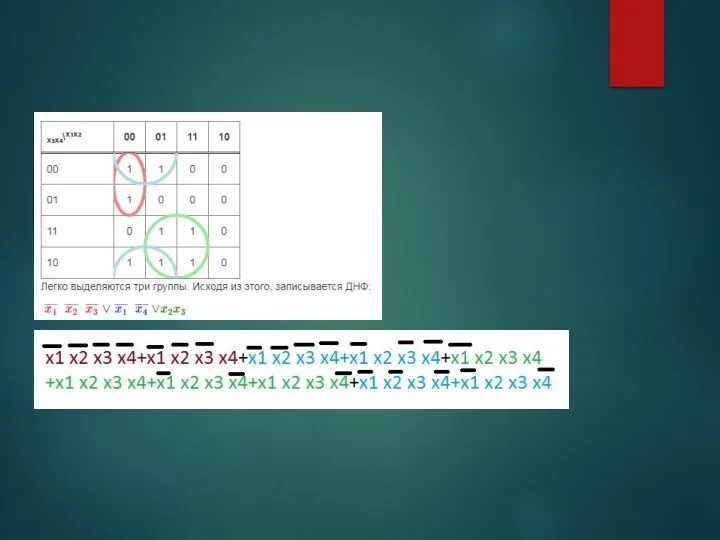
- 79. Таблица истинности в карте Карно
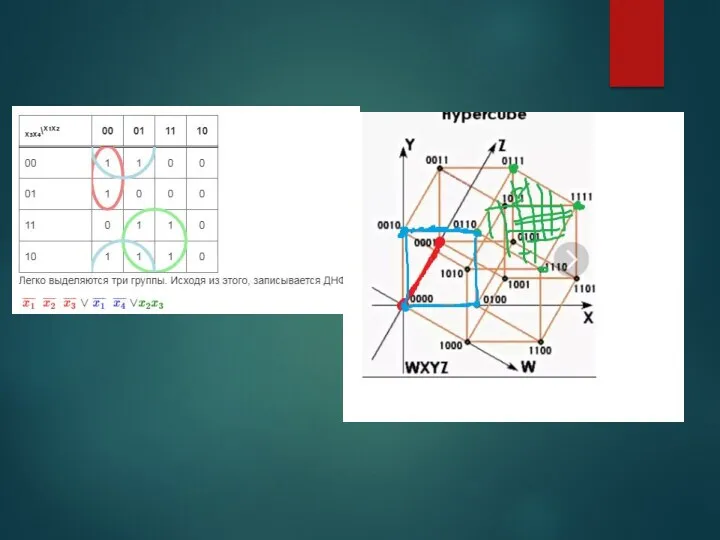
- 82. Геометрическая интерпретация логической функции для 4-ёх переменных.
- 83. Геометрическая интерпретация для логической функции для четырех переменных
- 84. В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в
- 85. =x1
- 92. Скачать презентацию










































































 Свойства прямоугольных треугольников
Свойства прямоугольных треугольников Тесты по математике 2 классЧисла от 1 до 100
Тесты по математике 2 классЧисла от 1 до 100 Образование чисел из одного десятка и нескольких единиц
Образование чисел из одного десятка и нескольких единиц Векторы в пространстве
Векторы в пространстве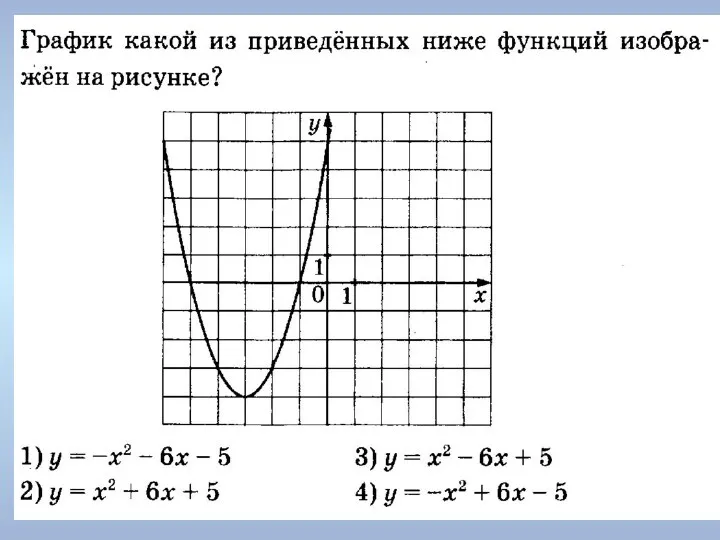 Графики. Парабола
Графики. Парабола Интерактивная игра по математике Собирай урожай
Интерактивная игра по математике Собирай урожай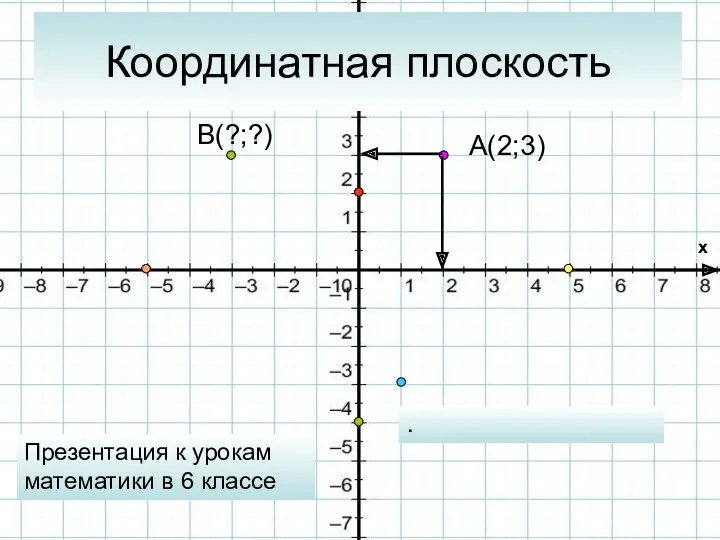 Координатная плоскость
Координатная плоскость Презентация к уроку математики по теме Умножение многозначных чисел на однозначное. 3 класс.
Презентация к уроку математики по теме Умножение многозначных чисел на однозначное. 3 класс. Делимое, делитель, частное
Делимое, делитель, частное Деление на 2. 2 класс
Деление на 2. 2 класс Таблица умножения. 3 класс.
Таблица умножения. 3 класс. Свойства прямоугольных треугольников
Свойства прямоугольных треугольников Решение линейных и квадратных уравнений. 9 класс
Решение линейных и квадратных уравнений. 9 класс Свойства степени с натуральным показателем
Свойства степени с натуральным показателем Задание 13 расстояние от точки до плоскости. Примеры решения задач
Задание 13 расстояние от точки до плоскости. Примеры решения задач Неравенства второй степени с одной переменной
Неравенства второй степени с одной переменной Наибольший общий делитель и наименьшее общее кратное чисел
Наибольший общий делитель и наименьшее общее кратное чисел Треугольник и его виды
Треугольник и его виды Физико–математический турнир для учащихся 10-11 классов
Физико–математический турнир для учащихся 10-11 классов Решения систем линейных уравнений. Метод подстановки и метод сложения. 7 класс
Решения систем линейных уравнений. Метод подстановки и метод сложения. 7 класс Презентация Вычитание. Название компонентов и результат действия
Презентация Вычитание. Название компонентов и результат действия Умножение и деление натуральных чисел. 5 класс
Умножение и деление натуральных чисел. 5 класс Интегрированные задачи. Математика + история. 8 класс
Интегрированные задачи. Математика + история. 8 класс Свойство умножения
Свойство умножения Презентация Способы прибавления и вычитания числа 4
Презентация Способы прибавления и вычитания числа 4 Додавання і віднімання числа 3. Переставний закон додавання. Урок №38. Математика
Додавання і віднімання числа 3. Переставний закон додавання. Урок №38. Математика Задачи со спичками
Задачи со спичками Методы решения тригонометрических уравнений. (Урок-лекция)
Методы решения тригонометрических уравнений. (Урок-лекция)