Содержание
- 2. Метод ветвей и границ Граф G = (V,E) – полный и задан матрицей весов. Будем считать,
- 3. Представим процесс построения маршрута в виде построения двоичного корневого дерева решений, в котором каждому узлу x
- 4. Тогда М(х) разбивается на 2 непересекающихся множества, в одно из которых можно отнести все маршруты, содержащие
- 5. Главное достоинство метода ветвей и границ в сравнении с полным перебором заключается в том, что активными
- 6. Правило активизации узлов: из множества узлов, не имеющих сыновей, в качестве активного выбирается узел с наименьшей
- 7. Процесс построения дерева решений продолжается до тех пор, пока активным не будет объявлен узел, для которого
- 8. Процедуру вычитания из каждого элемента строки (соответственно столбца) минимального элемента этой же строки (столбца) называют редукцией.
- 9. F – сумма всех констант, использованных при редукции. Тогда f является нижней границей всех маршрутов коммивояжёра
- 10. Раскраска графов Подмножество вершин графа называется независимым, если никакие вершины из этого подмножества не смежны. Во
- 11. Вершинной раскраской (далее - просто раскраской) графа называется отображение множества вершин графа на конечное множество цветов;
- 12. Хроматическим числом графа G называется минимальное число n=χ(G), такое, что существует правильная n-раскраска. Лемма 1. В
- 13. Теорема о пяти красках: Каждый планарный граф без петель и кратных ребер является не более чем
- 14. Рассмотрим планарный граф G без петель и кратных ребер с p0 вершинами; по лемме 1 в
- 15. Если в раскраске вершин v1...vk используется не более 4-х цветов, то "покрасим" вершину v0 в оставшийся
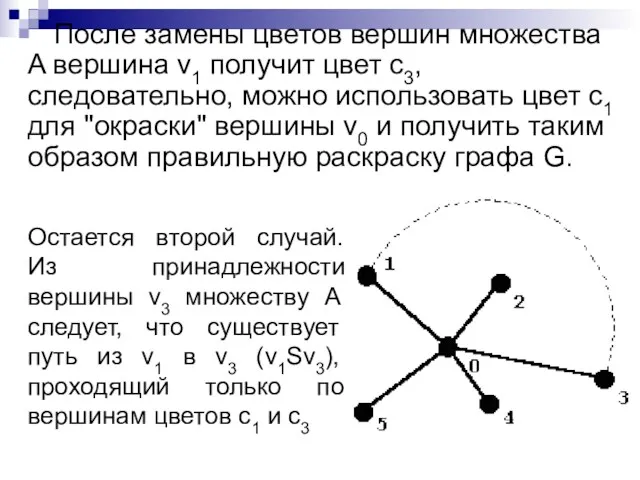
- 16. Возможны два случая: v3∉A; v3∈A. В первом случае поменяем цвета вершин множества A (c1↔c3); окраска при
- 17. После замены цветов вершин множества A вершина v1 получит цвет с3, следовательно, можно использовать цвет c1
- 18. Рассмотрим цикл L=v1Sv3(v3,v0)v0(v0,v1)v1 и замкнутую кривую, которая соответствует этому циклу в геометрической реализации графа. Вершина v2
- 19. Вершина v4 не принадлежит B, поскольку любой путь из v2 в v4 должен проходить, по крайней
- 20. Теорема о четырех красках. Каждый планарный граф без петель и кратных ребер является не более чем
- 21. Алгоритм раскраски графа Найти число связей всех вершин графа. Рассматривать вершины в порядке не возрастания числа
- 23. Скачать презентацию



















 Многомерная линейная регрессия
Многомерная линейная регрессия Урок математики по теме Свойства сложения, 2 класс
Урок математики по теме Свойства сложения, 2 класс Тройные интегралы
Тройные интегралы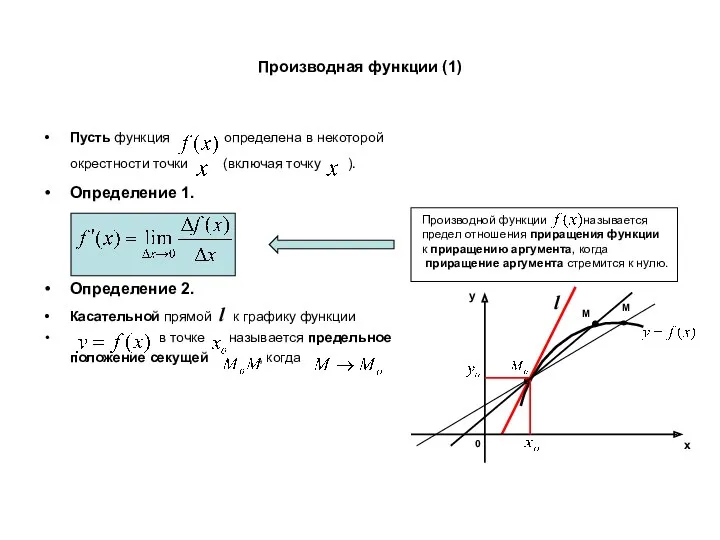 Производная функции
Производная функции Правило решения квадратных уравнений. Историческая справка
Правило решения квадратных уравнений. Историческая справка Отношения эквивалентности и порядка
Отношения эквивалентности и порядка Применение ленты Мёбиуса
Применение ленты Мёбиуса Проект по математике в 4 классе Мир в движении
Проект по математике в 4 классе Мир в движении Цилиндр. Определение цилиндра, развёртка цилиндра, формулы для вычисления
Цилиндр. Определение цилиндра, развёртка цилиндра, формулы для вычисления Давайте, посчитаем!
Давайте, посчитаем! Логикалық операциялар (дизъюнкция, конъюнкция, инверсия)
Логикалық операциялар (дизъюнкция, конъюнкция, инверсия) Методы оптимизации
Методы оптимизации Синус, косинус и тангенс острого угла прямоугольного треугольника
Синус, косинус и тангенс острого угла прямоугольного треугольника Электронный тренажёр по математике.
Электронный тренажёр по математике. Векторы. Сложение векторов
Векторы. Сложение векторов Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей проверка деления с остатком
проверка деления с остатком Параллельные прямые
Параллельные прямые Понятие формы. Многообразие форм окружающего мира
Понятие формы. Многообразие форм окружающего мира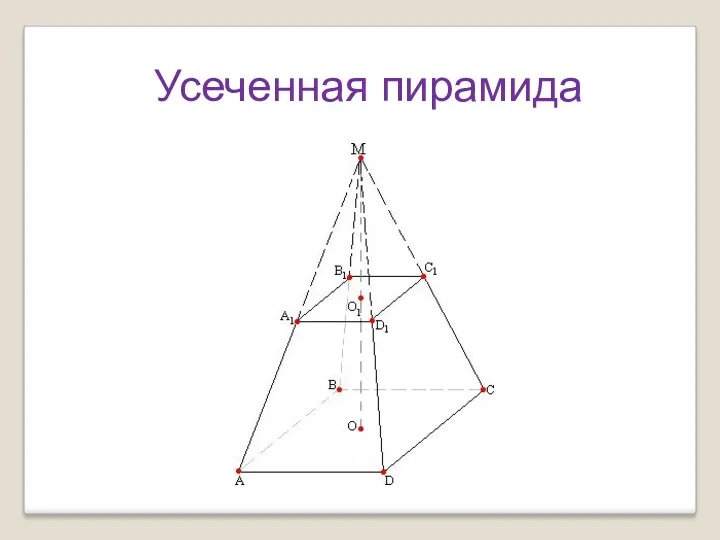 Усеченная пирамида
Усеченная пирамида Система линейных алгебраических уравнений (СЛАУ)
Система линейных алгебраических уравнений (СЛАУ) Деление дробей
Деление дробей Многогранники. Выпуклые и невыпуклые многогранники
Многогранники. Выпуклые и невыпуклые многогранники Принципы симметрии
Принципы симметрии Теория вероятностей. Статистические методы обработки информации
Теория вероятностей. Статистические методы обработки информации Распознавание и называние геометрических тел: куб, шар, пирамида, цилиндр
Распознавание и называние геометрических тел: куб, шар, пирамида, цилиндр Решение уравнений. 6 класс
Решение уравнений. 6 класс Взаимное расположение графиков линейных функций
Взаимное расположение графиков линейных функций