Содержание
- 2. СОДЕРЖАНИЕ ТЕОРЕТИЧЕСКОГО РАЗДЕЛА ДИСЦИПЛИНЫ ЛААГ Тема 1. Линейная алгебра Тема 2. Векторная алгебра Тема 3. Аналитическая
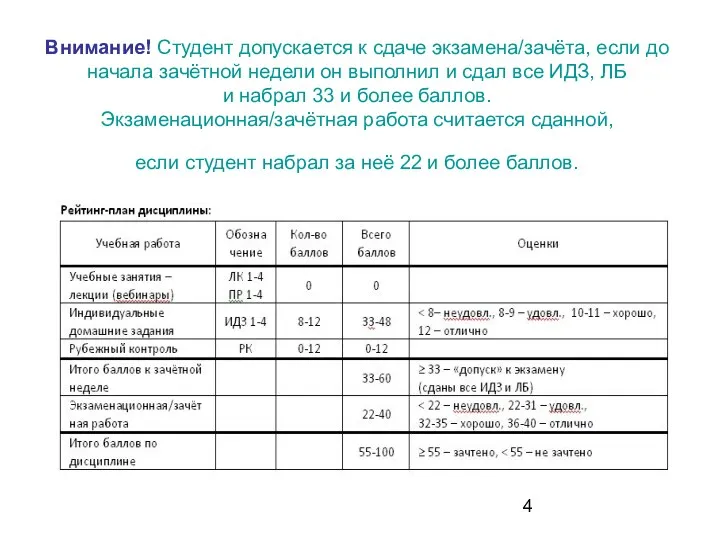
- 4. Внимание! Студент допускается к сдаче экзамена/зачёта, если до начала зачётной недели он выполнил и сдал все
- 5. Дополнительные Интернет- ресурсы Ссылка 1. http://portal.tpu.ru/SHARED/t/TOKTV/page_3
- 6. Дополнительные Интернет-ресурсы Ссылка 2. http://portal.tpu.ru/SHARED/t/TOKTV/Page_121
- 7. Тема 1. Линейная алгебра Разделы 1. Матрицы и действия над ними 2. Определители и их вычисление
- 8. Матрицы, определители и действия над ними
- 9. Виды матриц
- 10. Виды матриц
- 11. Произведение матриц
- 12. Произведение матриц
- 13. Произведение матрицы-строки на матрицу-столбец
- 14. Пример Можно ли умножить матрицы: (ответьте: 1) да или нет, 2)…)? 1) 2) 3)
- 15. Произведение матриц
- 16. Пример произведения матриц Задание. Найдите произведение матриц
- 17. Решение.
- 18. § Определители, их вычисление и свойства 1. Понятие определителя Определителем порядка n квадратной матрицы n-го порядка
- 19. Элементы, строки, столбцы матрицы называются соответственно элементами, строками, столбцами определителя матрицы. Определитель матрицы A обозначают |A|
- 20. Минором элемента определителя n-го порядка называется определитель (n–1)-го порядка, полученный из данного определителя вычеркиванием элементов i-й
- 21. Алгебраическим дополнением элемента называется минор этого элемента, умноженный на :
- 22. Теорема Лапласа. Определитель равен сумме произведений всех элементов любой строки (столбца) на их алгебраические дополнения, т.е.
- 23. Определитель второго порядка равен разности произведений элементов главной диагонали и элементов побочной диагонали.
- 24. Вычисление определителя третьего порядка
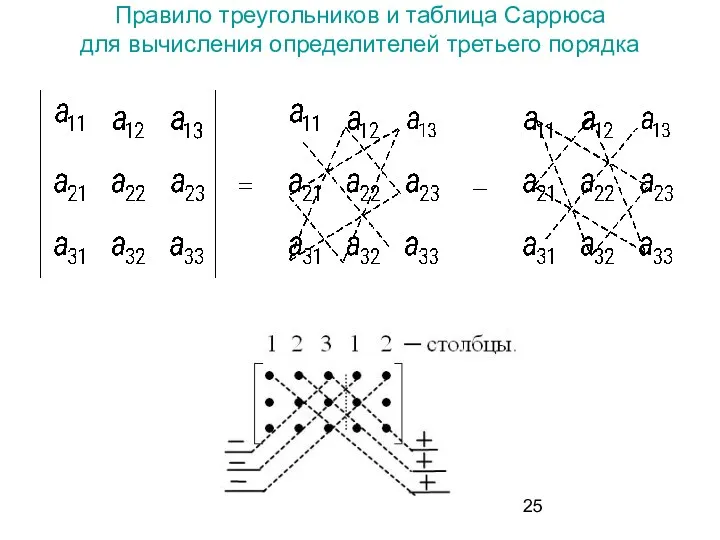
- 25. Правило треугольников и таблица Саррюса для вычисления определителей третьего порядка
- 26. Определитель треугольного вида равен произведению элементов главной диагонали
- 27. § Ранг матрицы 1. Понятие ранга матрицы. Теорема о базисном миноре Минором порядка k матрицы А
- 28. Минор Mk матрицы A называется её базисным минором, если он отличен от нуля, а все миноры
- 29. 2. Методы нахождения ранга матрицы 1) Метод окаймляющих миноров. Пусть Ms – минор порядка s. Окаймляющим
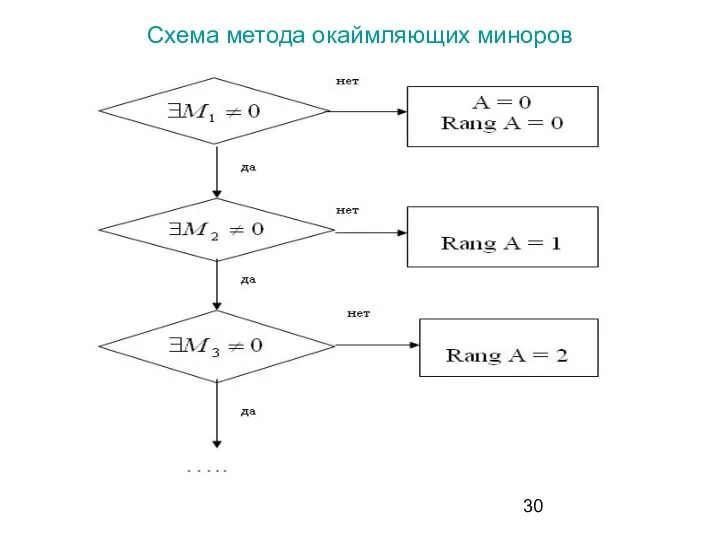
- 30. Схема метода окаймляющих миноров
- 31. 2) Метод элементарных преобразований. Элементарными преобразованиями матрицы называются преобразования следующего вида: а) умножение строки (столбца) на
- 32. ТЕОРЕМА. Эквивалентные матрицы имеют равные ранги. ТЕОРЕМА. Любая матрица A эквивалентна некоторой треугольной или трапециевидной матрице,
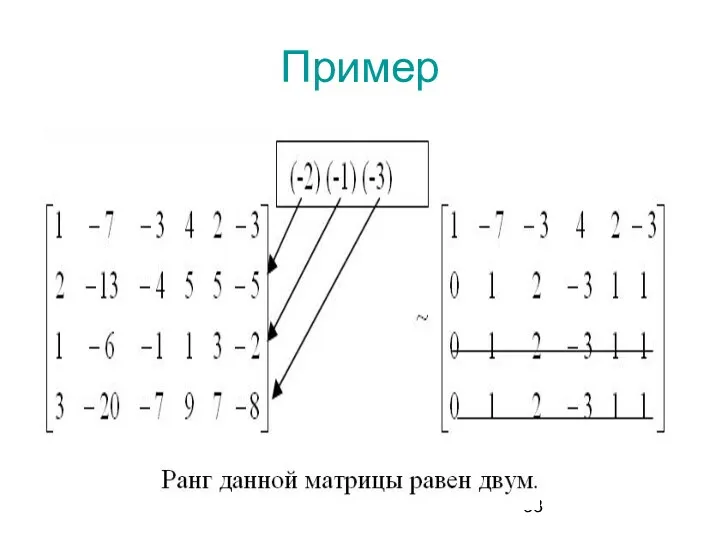
- 33. Пример
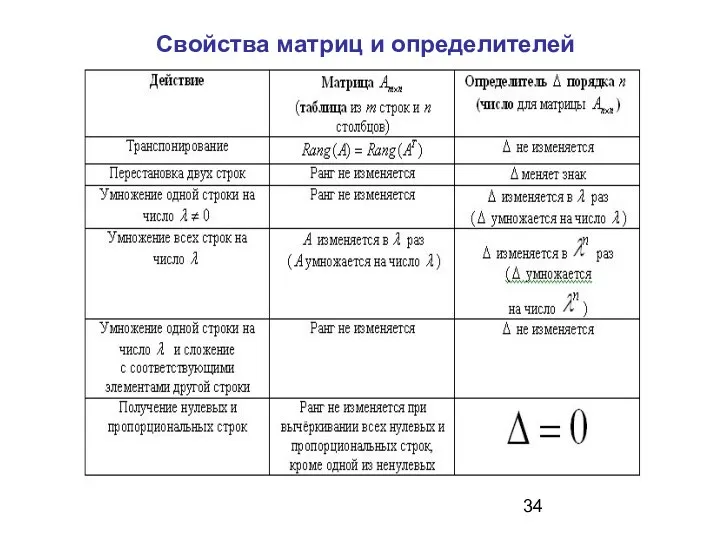
- 34. Свойства матриц и определителей
- 35. Вычисление определителей четвёртого и более высоких порядков 1. Выбрать рабочую строку (столбец) такую, где есть хотя
- 36. § Системы линейных уравнений 1. Основные понятия Уравнение называется линейным, если неизвестные в нём содержатся только
- 37. Рассмотрим систему m линейных уравнений с n неизвестными, т.е. систему вида
- 38. Обозначим через A и A* следующие матрицы: Матрицу A называют основной матрицей системы (1), матрицу A*
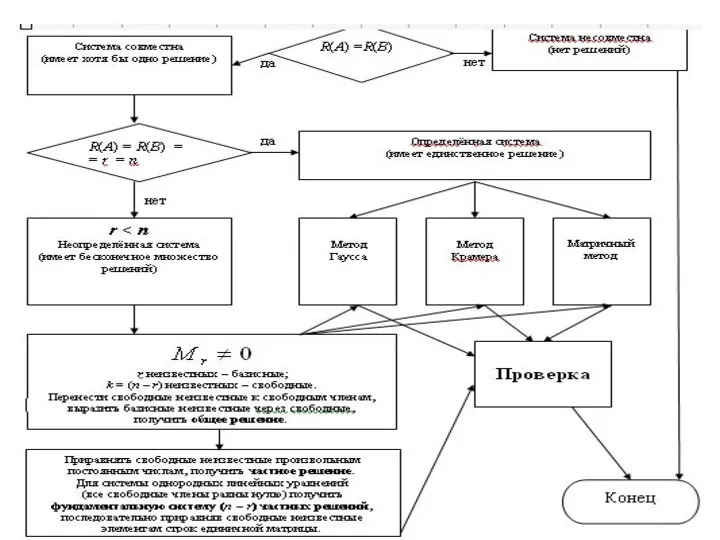
- 39. ТЕОРЕМА Кронекера – Капелли. Система линейных уравнений (1) совместна тогда и только тогда, когда ранг основной
- 40. 2. Методы решения систем линейных уравнений Матричный метод. ОПРЕДЕЛЕНИЕ. Обратной к матрице A называется матрица, обозначаемая
- 41. ТЕОРЕМА. Пусть A – квадратная матрица. Матрица A имеет обратную тогда и только тогда, когда её
- 42. Пример Решить систему уравнений матричным методом. Решение. Проверка!!!
- 43. Метод Крамера ТЕОРЕМА (Крамера). Если в системе линейных уравнений число уравнений m и число неизвестных n
- 44. Пример Решить систему уравнений методом Крамера. Решение. Проверка!!!
- 45. Метод Гаусса (метод исключения неизвестных) Две системы называются эквивалентными (равносильными), если их решения совпадают. К эквивалентной
- 46. Исключение неизвестных обычно осуществляют элементарными преобразованиями строк расширенной матрицы СЛУ. В результате расширенная матрица СЛУ приводится
- 47. Неизвестные, коэффициенты при которых вошли в базисный минор называются базисными неизвестными. Неизвестные, коэффициенты при которых не
- 48. Если n – число неизвестных системы, r – её ранг, то r неизвестных системы – базисные,
- 49. Если ранг основной и расширенной матриц СЛУ совпадает с числом неизвестных СЛУ, то свободных неизвестных нет.
- 50. Решение СЛУ, в котором базисные неизвестные выражены через свободные неизвестные, называется общим решением СЛУ. Решение, которое
- 51. Общее решение системы линейных уравнений можно получить, руководствуясь, например, следующим планом: а) выбрать базисный минор (обычно
- 53. Пример Решить систему уравнений методом Гаусса. Решение. Проверка!!!
- 55. Найти общее решение СЛУ и какое-либо частное решение СЛУ
- 56. Запишем эквивалентную СЛУ:
- 58. Скачать презентацию














































 Производная функции. Правила дифференцирования. Основные свойства дифференцируемых функций. Производные элементарных функций
Производная функции. Правила дифференцирования. Основные свойства дифференцируемых функций. Производные элементарных функций Презентация урока Составление и решение задач
Презентация урока Составление и решение задач Точки, прямые, отрезки. Задания для устного счета
Точки, прямые, отрезки. Задания для устного счета Приёмы устных вычислений трёхзначных чисел
Приёмы устных вычислений трёхзначных чисел Наглядное пособие по математике Объем прямоугольного параллелепипеда
Наглядное пособие по математике Объем прямоугольного параллелепипеда Параллельность прямых и плоскостей
Параллельность прямых и плоскостей презентация к уроку математики 4 класс Решение задач(школа 2100)
презентация к уроку математики 4 класс Решение задач(школа 2100) Многоугольники. Четырехугольники
Многоугольники. Четырехугольники Площадь. Формула площади прямоугольника
Площадь. Формула площади прямоугольника Решение задач. Урок математики для 4 класса
Решение задач. Урок математики для 4 класса Объем призмы. Решение задач
Объем призмы. Решение задач Обобщающий урок по теме: Деление обыкновенных дробей
Обобщающий урок по теме: Деление обыкновенных дробей Урок математики в 3 классе.
Урок математики в 3 классе. Trigonometry. Angles add to 180°
Trigonometry. Angles add to 180° Правильные многоугольники
Правильные многоугольники Метрические задачи. (Лекция 3)
Метрические задачи. (Лекция 3) Математика в живописи
Математика в живописи Разработка урока по математике во 2 классе по программе Школа России. Защита проекта Узоры и орнаменты на посуде.
Разработка урока по математике во 2 классе по программе Школа России. Защита проекта Узоры и орнаменты на посуде. Пропорции
Пропорции Дүниенің сәнін екі нәрсе келтіреді
Дүниенің сәнін екі нәрсе келтіреді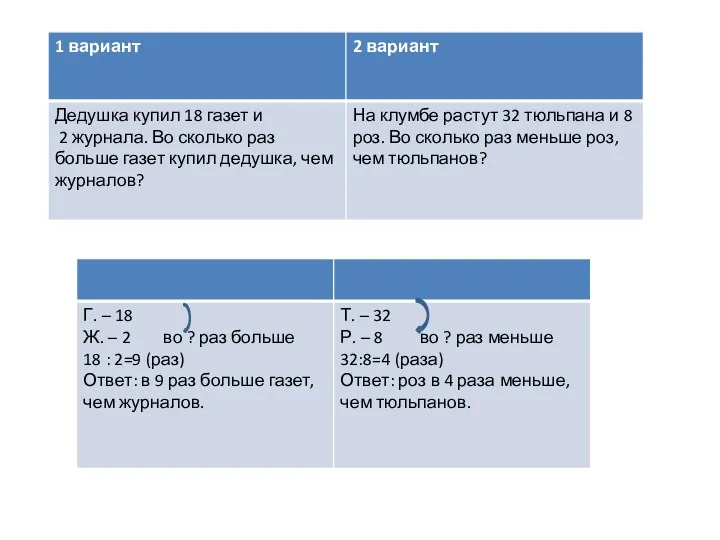 решение задач
решение задач Письменное сложение двузначных чисел без перехода через десяток
Письменное сложение двузначных чисел без перехода через десяток Построение графика функции Y = F(X+L) + M
Построение графика функции Y = F(X+L) + M Combinatorics. Permutations. Combinations. The binomial theorem
Combinatorics. Permutations. Combinations. The binomial theorem Сложение однозначных чисел с переходом через десяток
Сложение однозначных чисел с переходом через десяток Проценты. Решение задач
Проценты. Решение задач Общие методы решения тригонометрических уравнений
Общие методы решения тригонометрических уравнений Число π
Число π