Содержание
- 2. Цель урока. - Систематизировать и расширить знания, умения учащихся, связанных с применением методов решения тригонометрических уравнений.
- 3. Повторение теоретического материала. Функция называется четной, если f(x) = f(-x), где х и –х принадлежат области
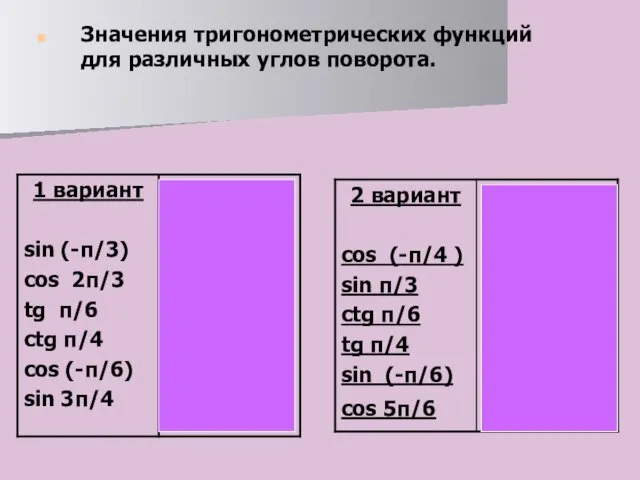
- 4. Значения тригонометрических функций для различных углов поворота.
- 5. Определение арксинуса, арккосинуса, арктангенса и арккотангенса.
- 6. Решение простейших тригонометрических уравнений вида sinx = а, cosx = а, tg х = а. х
- 7. . Методы решения тригонометрических уравнений - уравнения приводимые к линейным или квадратным уравнениям; - однородные тригонометрические
- 8. Уравнения приводимые к линейным или квадратным уравнениям. Уравнения вида A sin х + В sin х
- 9. Решим уравнение вида A sin2 х + В cos х + С =0: 2 sin2 х
- 10. Самостоятельное решение уравнений с последующей проверкой. 2
- 12. Однородные тригонометрические уравнения. Однородное тригонометрическое уравнение первой степени: A sin x+ B cos x = 0,
- 13. Однородное тригонометрическое уравнение второго порядка: А sin х + В sinх cos х + С cos
- 14. Решите уравнение 2 sin х - 3 sinх cos х - 5 cos х =0. Решение:
- 15. Самостоятельное решение уравнений с последующей проверкой. 2 2 2 2 2 2 2 2 2 2
- 16. Z.
- 17. Метод разложения на множители. Под разложением на множители понимается представление данного выражения в виде произведения нескольких
- 18. Решите уравнение: 2 sin x - cos 2x - sin x = 0 Решение: -сгруппируем первый
- 19. Что нового вы узнали на уроке? С какими трудностями встретились при решении уравнений? Какие темы необходимо
- 21. Скачать презентацию
















 Сказка – игра Волшебное число по теме: Решение уравнений 5 класс
Сказка – игра Волшебное число по теме: Решение уравнений 5 класс Нахождение нескольких долей целого.
Нахождение нескольких долей целого. Презентация к уроку математики по теме Умножение и деление чисел, оканчивающихся нулями
Презентация к уроку математики по теме Умножение и деление чисел, оканчивающихся нулями Деловая игра. Подготовка к ЕГЭ
Деловая игра. Подготовка к ЕГЭ Анимированная презентация для урока математики.(1класс)
Анимированная презентация для урока математики.(1класс) Производная по направлению. Градиент
Производная по направлению. Градиент Сложение и вычитание десятичных дробей. Урок 108
Сложение и вычитание десятичных дробей. Урок 108 Дружественные числа
Дружественные числа Математика. 1 класс. Урок 43. Уменьшаемое. Вычитаемое. Разность - Презентация
Математика. 1 класс. Урок 43. Уменьшаемое. Вычитаемое. Разность - Презентация Второй признак равенства треугольников
Второй признак равенства треугольников Деление на десятичную дробь. Правило деления
Деление на десятичную дробь. Правило деления Формулы сокращенного умножения. 7 класс
Формулы сокращенного умножения. 7 класс Презентация Игровые упражнения с геометрическими фигурами средняя группа
Презентация Игровые упражнения с геометрическими фигурами средняя группа Интерактивный тест. Готовимся к ОГЭ. 2 вариант
Интерактивный тест. Готовимся к ОГЭ. 2 вариант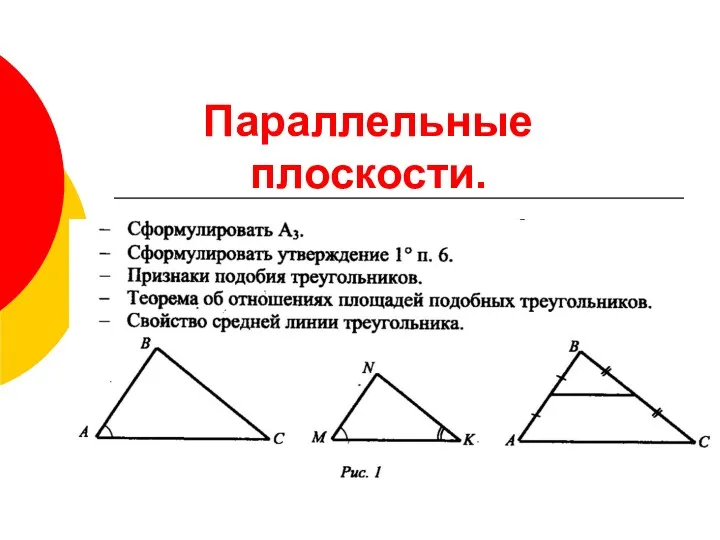 Параллельные плоскости
Параллельные плоскости Исторические комбинаторные задачи
Исторические комбинаторные задачи Презентация к занятию по ФЭМП Путешествие по сказке
Презентация к занятию по ФЭМП Путешествие по сказке Состав числа 10
Состав числа 10 Математическая игра Ключи от царства Математики
Математическая игра Ключи от царства Математики Язык геометрических рисунков
Язык геометрических рисунков Умножение числа 2
Умножение числа 2 группа комплексные числа
группа комплексные числа Дифференцированный подход в обучении на занятиях по математике с учётом развития речи
Дифференцированный подход в обучении на занятиях по математике с учётом развития речи Презентация Дроби. Нахождение части числа и нахождение числа по его части
Презентация Дроби. Нахождение части числа и нахождение числа по его части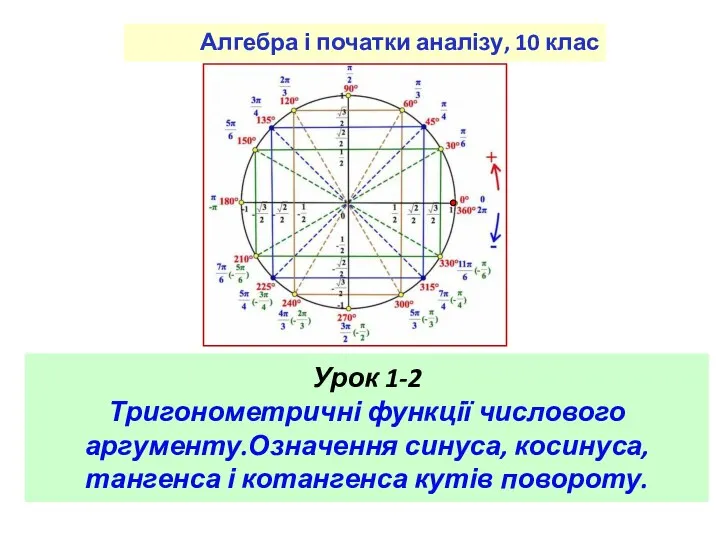 Тригонометричні функції числового аргументу. Означення синуса, косинуса, тангенса і котангенса кутів повороту. Урок 1-2
Тригонометричні функції числового аргументу. Означення синуса, косинуса, тангенса і котангенса кутів повороту. Урок 1-2 Электронное сопровождение заданий учебника математики 2 класса, часть 2 (автор Н. Б. Истомина)для фронтальной работы с интерактивной доской 4-я четверть
Электронное сопровождение заданий учебника математики 2 класса, часть 2 (автор Н. Б. Истомина)для фронтальной работы с интерактивной доской 4-я четверть Закрепление решения задач на движение. Новогоднее путешествие.
Закрепление решения задач на движение. Новогоднее путешествие. Обыкновенные дифференциальные уравнения
Обыкновенные дифференциальные уравнения